一、多目标粒子群算法简介
1 算法提出
虽然PSO算法在许多单目标优化问题中的成功应用说明了PSO算法的有效性.但是PSO算法不能直接应用于多目标优化问题, 因为多目标优化问题和单目标优化问题是有本质的区别的:前者一般是一组或几组连续解的集合, 而后者只是单个解或一组连续的解.另外, 遗传算法在多目标优化问题中的成功应用以及PSO算法和遗传算法的相似性, 说明PSO算法可能是一种处理多目标优化问题方法.但PSO算法和遗传算法还是有很大的不同:在遗传算法中染色体间共享信息, 是整个群体逐步移向好的区域, 而PSO算法中信息是由最好的粒子给出的, 其他个体跟着最好粒子快速向一点收敛.因此直接用PSO算法处理多目标优化问题, 将很容易收敛于非劣最优域的局部区域.
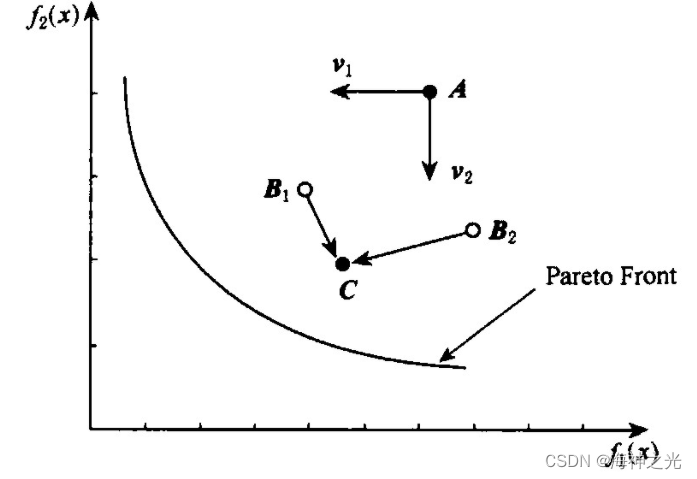
图1 目标函数空间
基于以上原因, 本文提出了最优解评估选取的PSO算法, 用于对多目标优化问题的非劣最优解集的搜索.算法在决策变量空间初始化一个粒子群, 通过多目标优化问题中的各个目标函数来共同指导粒子在决策变量空间中的飞行, 使其最终能落入非劣最优解集中;反映到目标函数空间, 粒子将落入非劣最优目标域.如图1为极小化f1 (x) , f2 (x) 时目标函数空间中情况.如果只有目标函数f1 (x) 或f2 (x) , 目标向量A将沿着v1或v2方向变化, 而算法中目标函数f1 (x) , f2 (x) 通过决策变量空间的粒子共同指导A的变化, 所以A既不沿v1方向变化, 也不沿v2方向变化, 而是从v1, v2间某一f1 (x) , f2 (x) 不同时增大的方向变化, 最终到达非劣最优目标域.具体通过下述方式实现:首先, 用多目标优化问题中的各个目标函数, 找到每个粒子对应于各个目标函数的全局极值gBest[i] (其中, i=1, 2, …, n是目标函数的个数) 和个体极值pBest[i, j] (其中, j=1, 2, …, N是粒子个数) .其次, 在更新每个粒子的速度时, 用各个gBest[i]的“均值”作为全局极值gBest;每个粒子的pBest[i, j]是通过判断pBest[i, j]相对于gBest[i]的离散程度决定是取pBest[i, j]的均值还是在pBest[i, j]中随机选取.
2 算法分析
因为在PSO算法中每个粒子的行为主要由gBest和pBest决定, 所以本文的选取方式使得每个粒子向解移动时的行为各不相同:每个粒子都移向解区域中不同的解.这样最终整个群体将分散于非劣最优解集中, 避免了收敛于非劣最优解集的局部区域.gBest的评估选取在避免了所有个体落于某一目标函数的最优点的同时, 更重要是体现了各个目标函数间的制约关系, 而pBest的选取方式更加强了这一行为.
如图2为极小化f1 (x) , f2 (x) 时某次循环后决策变量空间中情况.群体对目标函数f1 (x) 而言的最好解为x1 (gBest[1]) , x2为f2 (x) 的最好解gBest[2].对应于x1, x2在目标函数空间的目标向量为B1, B2 (如图1) .依据算法对gBest[1], gBest[2]评估选取得到gBest, 对应的解一定会在x1, x2之间, 假设为x0 (如图2) , 而在目标函数空间与x0对应的目标向量为C.显然C要比B1, B2更接近非劣最优目标域, 这也说明用x0 (gBest) 更新粒子要比用gBest[1]或gBest[2]更好.和标准的PSO算法相比, 本文是对粒子的全局极值和个体极值的选取做了改进.
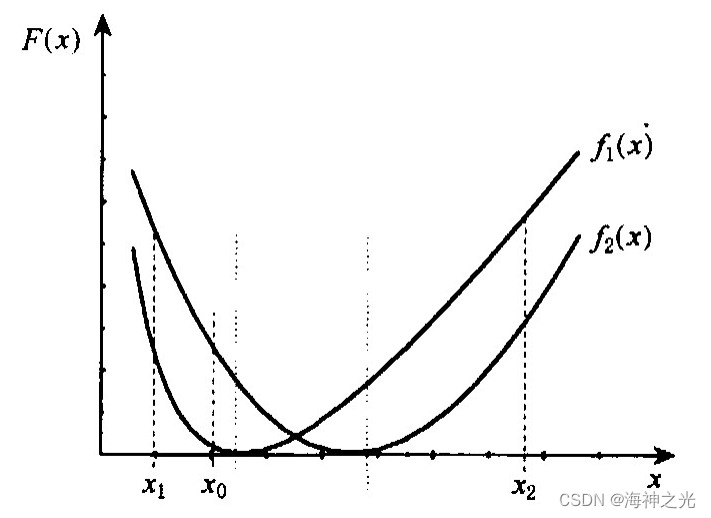
图2 决策变量空间
3 算法流程
下面以两目标函数 (极小化f1 (x) , f2 (x) ) 优化为例给出算法流程 (没有给出对粒子的每个维度的操作, 实际使用时可参考PSO算法的公式进行) .
① 初始化粒子群:给定群体规模N, 随机产生每个粒子的位置Xi、速度Vi.
② 用目标函数f1 (x) , f2 (x) 分别计算每个粒子的适应度值:
For i=1 to N
Fitness1[i]=f1 (X[i]) ;
Fitness2[i]=f2 (X[i]) ;
Next i
③ 在两个目标函数f1 (x) , f2 (x) 下分别对每个粒子求得个体极值:
For i=1 to N
pBest[1, i]←f1 (x) ;
pBest[2, i]←f2 (x) ;
Next i
④ 对两个目标函数f1 (x) , f2 (x) 分别求两个全局极值:
gBest[1]←f1 (x) ;
gBest[2]←f2 (x) ;
⑤ 计算两全局矢量的均值gBest和距离dgBest:
gBest=Average (gBest[1], gBest[2]) ;
dgBest=Distance (gBest[1], gBest[2]) ;
⑥ 计算每个粒子pBest[1, i]和pBest[2, i]之间的距离dpBest[i]:
For i=1 to N
dpBest[i]=Distance (pBest[1, i],
pBest[2, i]) ;
Next i
⑦ 对每个粒子计算更新速度Vi和位置Xi时所要用的个体极值pBest[i]:

⑧ 用⑤⑦所得的gBest和pBest[i]更新每个粒子速度Vi和位置Xi;
⑨ 如满足中止条件, 退出, 否则返回②.
说明:函数Average () 既可以是平均也可以是按一定比例动态选取.
二、部分源代码
三、运行结果






四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]张利彪,周春光,马铭,刘小华.基于粒子群算法求解多目标优化问题[J].计算机研究与发展. 2004,(07)
