# !/usr/bin/env python
# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
font = {'family': 'SimSun', # 宋体
# 'weight': 'bold', # 加粗
'size': '10.5' # 五号
}
plt.rc('font', **font)
plt.rc('axes', unicode_minus=False)
# plt.rcParams['figure.facecolor'] = "#FFFFF0" # 设置窗体颜色
# plt.rcParams['axes.facecolor'] = "#FFFFF0" # 设置绘图区颜色
class Kf_Params:
B = 0 # 外部输入为0
u = 0 # 外部输入为0
K = float('nan') # 卡尔曼增益无需初始化
z = float('nan') # 这里无需初始化,每次使用kf_update之前需要输入观察值z
P = np.diag(np.ones(4)) # 初始P设为0 ??? zeros(4, 4)
# 初始状态:函数外部提供初始化的状态,本例使用观察值进行初始化,vx,vy初始为0
x = []
G = []
# 状态转移矩阵A
# 和线性系统的预测机制有关,这里的线性系统是上一刻的位置加上速度等于当前时刻的位置,而速度本身保持不变
A = np.eye(4) + np.diag(np.ones((1, 2))[0, :], 2)
# 预测噪声协方差矩阵Q:假设预测过程上叠加一个高斯噪声,协方差矩阵为Q
# 大小取决于对预测过程的信任程度。比如,假设认为运动目标在y轴上的速度可能不匀速,那么可以把这个对角矩阵
# 的最后一个值调大。有时希望出来的轨迹更平滑,可以把这个调更小
Q = np.diag(np.ones(4)) * 0.1
# 观测矩阵H:z = H * x
# 这里的状态是(坐标x, 坐标y, 速度x, 速度y),观察值是(坐标x, 坐标y),所以H = eye(2, 4)
H = np.eye(2, 4)
# 观测噪声协方差矩阵R:假设观测过程上存在一个高斯噪声,协方差矩阵为R
# 大小取决于对观察过程的信任程度。比如,假设观测结果中的坐标x值常常很准确,那么矩阵R的第一个值应该比较小
R = np.diag(np.ones(2)) * 0.1
def kf_init(px, py, vx, vy):
# 本例中,状态x为(坐标x, 坐标y, 速度x, 速度y),观测值z为(坐标x, 坐标y)
kf_params = Kf_Params()
kf_params.B = 0
kf_params.u = 0
kf_params.K = float('nan')
kf_params.z = float('nan')
kf_params.P = np.diag(np.ones(4))
kf_params.x = [px, py, vx, vy]
kf_params.G = [px, py, vx, vy]
kf_params.A = np.eye(4) + np.diag(np.ones((1, 2))[0, :], 2)
kf_params.Q = np.diag(np.ones(4)) * 0.1
kf_params.H = np.eye(2, 4)
kf_params.R = np.diag(np.ones(2)) * 0.1
return kf_params
def kf_update(kf_params):
# 以下为卡尔曼滤波的五个方程(步骤)
a1 = np.dot(kf_params.A, kf_params.x)
a2 = kf_params.B * kf_params.u
x_ = np.array(a1) + np.array(a2)
b1 = np.dot(kf_params.A, kf_params.P)
b2 = np.dot(b1, np.transpose(kf_params.A))
p_ = np.array(b2) + np.array(kf_params.Q)
c1 = np.dot(p_, np.transpose(kf_params.H))
c2 = np.dot(kf_params.H, p_)
c3 = np.dot(c2, np.transpose(kf_params.H))
c4 = np.array(c3) + np.array(kf_params.R)
c5 = np.linalg.matrix_power(c4, -1)
kf_params.K = np.dot(c1, c5)
d1 = np.dot(kf_params.H, x_)
d2 = np.array(kf_params.z) - np.array(d1)
d3 = np.dot(kf_params.K, d2)
kf_params.x = np.array(x_) + np.array(d3)
e1 = np.dot(kf_params.K, kf_params.H)
e2 = np.dot(e1, p_)
kf_params.P = np.array(p_) - np.array(e2)
kf_params.G = x_
return kf_params
def accuracy(predictions, labels):
return np.array(predictions) - np.array(labels)
if __name__ == '__main__':
# 真实路径
path = './9.xlsx'
data_A = pd.read_excel(path, header=None)
data_A_x = list(data_A.iloc[::, 0])
data_A_y = list(data_A.iloc[::, 1])
A = np.array(list(zip(data_A_x, data_A_y)))
# plt.subplot(131)
plt.figure()
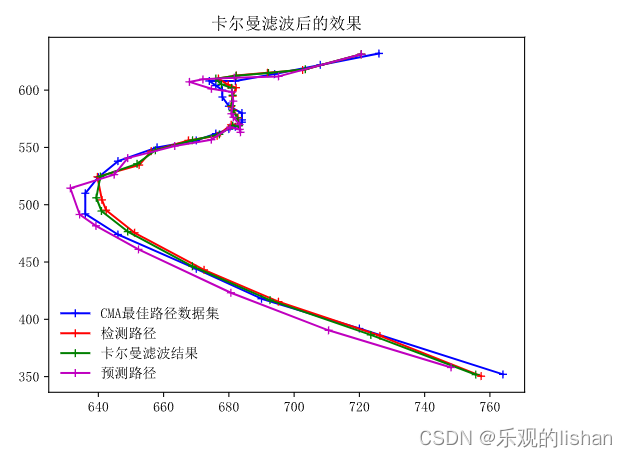
plt.plot(data_A_x, data_A_y, 'b-+')
# plt.title('实际的真实路径')
# 检测到的路径
path = './10.xlsx'
data_B = pd.read_excel(path, header=None)
data_B_x = list(data_B.iloc[::, 0])
data_B_y = list(data_B.iloc[::, 1])
B = np.array(list(zip(data_B_x, data_B_y)))
# plt.subplot(132)
plt.plot(data_B_x, data_B_y, 'r-+')
# plt.title('检测到的路径')
# 卡尔曼滤波
kf_params_record = np.zeros((len(data_B), 4))
kf_params_p = np.zeros((len(data_B), 4))
t = len(data_B)
kalman_filter_params = kf_init(data_B_x[0], data_B_y[0], 0, 0)
for i in range(t):
if i == 0:
kalman_filter_params = kf_init(data_B_x[i], data_B_y[i], 0, 0) # 初始化
else:
# print([data_B_x[i], data_B_y[i]])
kalman_filter_params.z = np.transpose([data_B_x[i], data_B_y[i]]) # 设置当前时刻的观测位置
kalman_filter_params = kf_update(kalman_filter_params) # 卡尔曼滤波
kf_params_record[i, ::] = np.transpose(kalman_filter_params.x)
kf_params_p[i, ::] = np.transpose(kalman_filter_params.G)
kf_trace = kf_params_record[::, :2]
kf_trace_1 = kf_params_p[::, :2]
# plt.subplot(133)
plt.plot(kf_trace[::, 0], kf_trace[::, 1], 'g-+')
plt.plot(kf_trace_1[1:26, 0], kf_trace_1[1:26, 1], 'm-+')
legend = ['CMA最佳路径数据集', '检测路径', '卡尔曼滤波结果', '预测路径']
plt.legend(legend, loc="best", frameon=False)
plt.title('卡尔曼滤波后的效果')
plt.savefig('result.svg', dpi=600)
plt.show()
# plt.close()
p = accuracy(kf_trace, A)
print(p)
?
