计算图_非标量调用backward()求梯度
当y不是标量时,向量y关于向量x的导数的最自然解释是一个矩阵。对于高阶和高维的y和x,求导的结果可以是一个高阶张量。
然而,虽然这些更奇特的对象确实出现在高级机器学习中(包括深度学习中),但当我们调用向量的反向计算时,我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。这里,我们的目的不是计算微分矩阵,而是批量中每个样本单独计算的偏导数之和。
x = torch.arange(4.0)
x.requires_grad = True
y = x * x
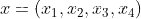
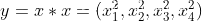
方法1:通过y.sum().backward()调用反向传播
y.sum().backward()
print(x.grad)
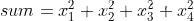
sum为y.sum()

把x带入得 x.grad为(0,2,4,8)
一个向量是不进行backward操作的,而sum()后,由于梯度为1,所以对结果不产生影响。反向传播算法一定要是一个标量才能进行计算。
方法2:传入shape和x一样的ones参数
y.backward(torch.ones(x.shape))
print(x.grad)
通过雅可比矩阵进行向量对向量的求导

带入x得出
torch.ones(x.shape)创造的向量为(1,1,1,1)
相乘得到x.grad = (0,2,4,6)
detach()
返回一个新的tensor,从当前计算图中分离下来的,但是仍指向原变量的存放位置(内存相同),不同之处只是requires_grad为false,得到的这个tensor不再有计算梯度的能力,反向传播时遇到该tensor将停止,不再继续传播
新tensor不能求梯度,若不修改新tensor则被detach()的张量还能求梯度
对backword()的理解
backward是通过反向传播函数来求梯度
import torch
a = torch.randn(size=(), requires_grad=True)
b = torch.randn(size=(), requires_grad=True)
c = torch.randn(size=(), requires_grad=True)
c = a * b
c.backward()
print( a.grad == b,a)
print( b.grad == a,b)
output:
tensor(True) tensor(-0.7874, requires_grad=True)
tensor(True) tensor(0.0025, requires_grad=True)
若在 torch 中 对定义的变量 requires_grad 的属性赋为 True ,那么此变量即可进行梯度以及导数的求解,在以上代码中,a,b,c 都可以理解为数学中的x,y,z进行运算,c 分别对 a,b 求导的结果为 b,a。
当c.backward() 语句执行后,会自动对 c 表达式中 的可求导变量进行方向导数的求解,并将对每个变量的导数表达存储到 变量名.grad 中。
