Residual Net
首先下图为一个简单的残差连接,我们先不介绍具体内涵,而是讨论一下为什么需要残差连接?
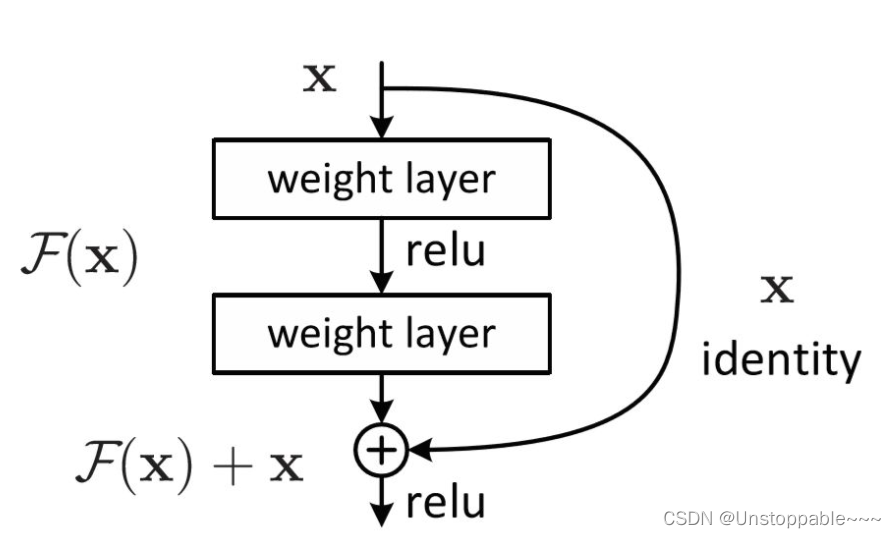
注意:googlenet在这里是拼接,resnet是相加
为什么要引入残差连接?
首先大家已经形成了一个通识,在一定程度上,网络越深表达能力越强,性能越好。
不过,好是好了,随着网络深度的增加,带来了许多问题:
- 计算资源的消耗
- 模型容易过拟合
- 梯度消失/梯度爆炸问题的产生
在resnet出来之前大家没想办法去解决吗?当然不是。更好的优化方法,更好的初始化策略,BN层,Relu等各种激活函数,甚至使用GPU集群等方法,都被用过了,但是仍然不够,改善问题的能力有限,然而随着网络层数的增加,网络发生了退化现象:随着网络层数的增多,训练集loss逐渐下降,然后趋于饱和,当你再增加网络深度的话,训练集loss反而会增大。注意这并不是过拟合,因为在过拟合中训练loss是一直减小的。直到残差连接被广泛使用,这一问题才被解决。
反向传播示例如下所示:
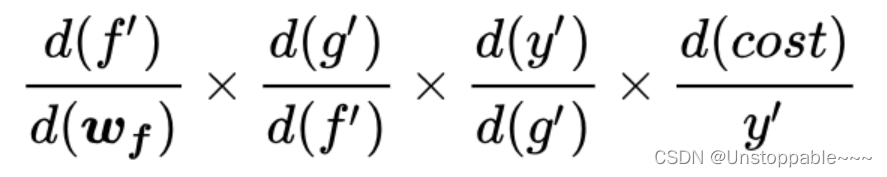
它有隐患,一旦其中某一个导数很小,多次连乘后梯度可能越来越小,这就是常说的梯度消散,对于深层网络,传到浅层几乎就没了。但是如果使用了残差,每一个导数就加上了一个恒等项1,dh/dx=d(f+x)/dx=1+df/dx。此时就算原来的导数df/dx很小,这时候误差仍然能够有效的反向传播,这就是核心思想。
由此我们产生思考:
当网络退化时,浅层网络能够达到比深层网络更好的训练效果,这时如果我们把低层的特征传到高层,那么效果应该至少不比浅层的网络效果差,或者说如果一个VGG-100网络在第98层使用的是和VGG-16第14层一模一样的特征,那么VGG-100的效果应该会和VGG-16的效果相同。所以,我们可以在VGG-100的98层和14层之间添加一条直接映射来达到此效果。
从信息论的角度讲,由于DPI(数据处理不等式)的存在,在前向传输的过程中,随着层数的加深,Feature Map包含的图像信息会逐层减少,而ResNet的直接映射的加入,保证了 L+1层的网络一定比L层包含更多的图像信息。
基于这种使用直接映射来连接网络不同层直接的思想,残差网络应运而生。
总结:
**作者们认为神经网络的退化才是难以训练深层网络根本原因所在,而不是梯度消散。**虽然梯度范数大,但是如果网络的可用自由度对这些范数的贡献非常不均衡,也就是每个层中只有少量的隐藏单元对不同的输入改变它们的激活值,而大部分隐藏单元对不同的输入都是相同的反应,此时整个权重矩阵的秩不高。并且随着网络层数的增加,连乘后使得整个秩变的更低。
残差网络结构解析
ResNet的整体结构类似于VGG和GoogleNet的总体框架,其中替换成了ResNet块。
残差网络是由一系列残差块组成的(如下式)。一个残差块可以用表示为:
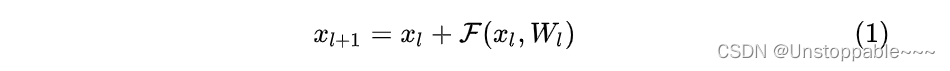
下一层的输入是由上一层的输出直接加上残差得到。
残差块分成两部分直接映射部分和残差部分。h(Xl)是直接映射,反应在下图中是左边的直线; [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传F(Xl, Wl)是残差部分,一般由两个或者三个卷积操作构成,即下图中右侧包含卷积的部分。
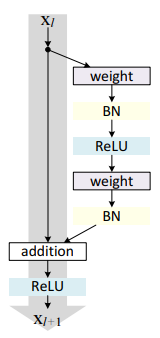
注:Weight在卷积网络中是指卷积操作,addition是指单位加操作。
由此我们可以看出Resnet可以叠加到1000层的原因:下的一层的信息直接接收到了上一层的信息,信息损失较少,可用于深度的网络结构。
在卷积网络中,Xl可能和Xl+1的Feature Map的数量不一样,这时候就需要使用1 * 1卷积进行升维或者降维(式2)。这时,残差块表示为:
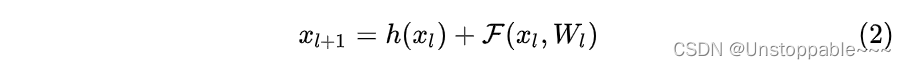
其中h(Xl) = W’lX。其中W’l是 1×1 卷积操作,但是实验结果 1×1 卷积对模型性能提升有限,所以一般是在升维或者降维时才会使用。
在这里,1×1的卷积可以降低运算量同时不损失太多信息,通常我们使用多个卷积核对特征进行提取(不同卷积核提取到不同的特征),若原图中的信息量不多(特征很少)我们通过多种卷积核得到的特征图一定是稀疏的,就可以使用1*1的卷积核进行降维(因为矩阵稀疏,压缩后,损失的信息也很少),进行一定操作之后,再重新升维即可。
残差块的实现
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Residual(nn.Module):
def __init__(self, input_channels, num_channels,
use_1x1conv=False, strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels,
kernel_size=3, padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels,
kernel_size=3, padding=1)
if use_1x1conv: #若使用1*1卷积层
self.conv3 = nn.Conv2d(input_channels, num_channels,
kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X #在这里实现了直接映射和残差映射的相加,实现了一个残差块
return F.relu(Y)
上述代码可以生成两种类型的网络: 一种是当use_1x1conv=False时,应用ReLU非线性函数之前,将输入添加到输出。 另一种是当use_1x1conv=True时,添加通过1×1卷积调整通道和分辨率。
ResNet模型实现
ResNet的前两层跟之前介绍的GoogLeNet中的一样: 在输出通道数为64、步幅为2的7×7卷积层后,接步幅为2的3×3的最大汇聚层。 不同之处在于ResNet每个卷积层后增加了批量规范化层。
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
ResNet则使用4个由残差块组成的模块,每个模块使用若干个同样输出通道数的残差块。 第一个模块的通道数同输入通道数一致。 由于之前已经使用了步幅为2的最大汇聚层,所以无须减小高和宽。 之后的每个模块在第一个残差块里将上一个模块的通道数翻倍,并将高和宽减半。
def resnet_block(input_channels, num_channels, num_residuals,
first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(Residual(input_channels, num_channels,
use_1x1conv=True, strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))
net = nn.Sequential(b1, b2, b3, b4, b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(), nn.Linear(512, 10))
每个模块有4个卷积层(不包括恒等映射的1×1卷积层)。 加上第一个7×7卷积层和最后一个全连接层,共有18层。 因此,这种模型通常被称为ResNet-18。
