2 数据预处理
数据预处理的过程:输入数据——>模型——>输出数据
数据样本矩阵【一行一样本,一列一特征】
| 年龄 | 学历 | 经验 | 性别 | 月薪 |
|---|---|---|---|---|
| 25 | 硕士 | 2 | 女 | 10000 |
| 20 | 本科 | 3 | 男 | 8000 |
| … | … | … | … | … |
数据预处理相关库:
# 解决机器学习问题的科学计算工具包---数据预处理库
import sklearn.preprocessing as sp
【机器学习基础】Python数据预处理:彻底理解标准化和归一化
2.1 均值移除(标准化)
由于一个样本的不同特征值差异较大,不利于使用现有机器学习算法进行样本处理
均值移除(标准化):让样本矩阵中的每一列的均值为0,标准差为1
转换公式: x i ′ = x i ? μ σ {x_i^{'}}=\frac{{x_i-\mu}}{\sigma} xi′?=σxi??μ?
如何使样本矩阵中的每一列的平均值为0呢?
# 例如有一列特征值表示年龄:[17,20,23]
mean=(17+20+23)/3=20
a'=17-20=-3
b'=20-20=0
c'=23-20=3
# 完成!
如何使样本矩阵中的每一列的标准差为1呢?
a'=-3
b'=0
c'=3
s'=std(a',b',c')
[a'/s',b'/s',c'/s']
# 完成!
均值移除(标准化)API:
import sklearn.preprocessing as sp
# scale函数用于对数据进行预处理,实现均值移除(标准化)
# 返回A为均值移除(标准化)后的结果
A=sp.scale(原始样本矩阵)
案例:
import numpy as np
# 数据预处理库
import sklearn.preprocessing as sp
raw_samples=np.array([
[17,90,4000],
[20,80,5000],
[23,75,5500]])
# 均值移除(标准化)
result=sp.scale(raw_samples)
# axis:轴向,axis=0:按列运算
print(result.mean(axis=0))
print(result.std(axis=0))
result
2.2 范围(特征)缩放
范围(特征)缩放:将样本矩阵中的每一列的最小值和最大值设定为相同的区间,统一各列特征值的范围
一般情况下会把特征值缩放至[0,1]区间
转换公式: x i ′ = x i ? x m i n x m a x {x_i^{'}}=\frac{{x_i-x_{min}}}{x_{max}} xi′?=xmax?xi??xmin??
如何使一组特征值的最小值为0呢?
# 例如有一列特征值表示年龄:
[17,20,23]
# 每个元素减去特征值数组所有元素的最小值即可:
17-17=0
20-17=3
23-17=6
[0,3,6]
# 完成!
如何使一组特征值的最大值为1呢?
[0,3,6]
# 特征值数组的每个元素除以最大值即可:
0/6=0
3/6=1/2
6/6=1
[0,1/2,1]
# 完成!
范围(特征)缩放API:
import sklearn.preprocessing as sp
# 创建MinMax缩放器
mms=sp.MinMaxScaler(feature_range=(0,1))
# 调用mms对象的方法执行缩放操作,返回缩放后的结果
result=mms.fit_transform(原始样本矩阵)
案例:
# 调用数据预处理库实现
import numpy as np
# 数据预处理库
import sklearn.preprocessing as sp
raw_samples=np.array([
[17,90,4000],
[20,80,5000],
[23,75,5500]])
# 范围(特征)缩放
mms=sp.MinMaxScaler(feature_range=(0,1))
result=mms.fit_transform(raw_samples)
result
17 k + b = 0 23 k + b = 1 \begin{array}{l} 17k + b = 0\\ 23k + b = 1 \end{array} 17k+b=023k+b=1?
[ 17 1 23 1 ] [ k b ] = [ 0 1 ] \left[ {\begin{array}{cc} {17}&1\\ {23}&1 \end{array}} \right]\left[ {\begin{array}{cc} k\\ b \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{cc} 0\\ 1 \end{array}} \right] [1723?11?][kb?]=[01?]
案例:
# 未调用数据预处理库,手动计算实现
import numpy as np
raw_samples=np.array([
[17,90,4000],
[20,80,5000],
[23,75,5500]])
print(raw_samples)
print("\n",raw_samples.T)
new_samples=[]
# raw_samples.T:矩阵转置,即列变为行,取得每行最小值和最大值,也就是原始矩阵的每列最小值和最大值
for row in raw_samples.T:
min_val=row.min()
max_val=row.max()
# 整理求出缩放线性关系(y=kx+b,即xk+b=y)所需要的矩阵:A与B
A=np.array([
[min_val,1],
[max_val,1]
])
B=np.array([0,1])
# np.linalg.solve(A,B):解方程组:用于求解形如AX=B的方程组
# X的shape(形状)与B一样,X:参数k和b的值,k=X[0],b=X[1]
X=np.linalg.solve(A,B)
print("\n",X)
new_row=row*X[0]+X[1]
new_samples.append(new_row)
# 转置显示原始样本矩阵的范围缩放结果
print("\n",np.array(new_samples).T)
2.3 归一化
有些情况每个样本的每个特征值具体的值并不重要,但是每个样本特征值的占比更加重要
| 动画 | 剧情 | 爱情 | |
|---|---|---|---|
| 张三 | 10 | 20 | 5 |
| 李四 | 2 | 4 | 1 |
| 老王 | 11 | 13 | 18 |
归一化:用每个样本的每个特征值除以该样本各个特征值绝对值的总和
变换后的样本矩阵,每个样本的特征值绝对值之和为1
转换公式: x i ′ = x i ∑ i = 1 n ∣ x i ∣ {x_i^{'}}=\frac{{{x_i}}}{{\sum\limits_{i=1}^n{\left|{{x_i}}\right|}}} xi′?=i=1∑n?∣xi?∣xi??
归一化相关API:
import sklearn.preprocessing as sp
# norm 范数
# l1---L1范数:向量中的各个元素绝对值之和
# l2---L2范数:向量中的各个元素平方之和
# 返回归一化预处理后的样本矩阵
sp.normalize(原始样本矩阵,norm='l1')
案例:
import numpy as np
# 数据预处理库
import sklearn.preprocessing as sp
samples=np.array([
[10,21,5],
[2,4,1],
[11,18,18]])
# 转换数据类型
samples=samples.astype(np.float64)
# 方式1:
# 归一化
# L1范数:向量中的元素绝对值之和
result=sp.normalize(samples,norm='l1')
# axis:轴向,axis=1:按行运算
print(abs(result).sum(axis=1))
print(result)
# 方式2:
for row in samples:
# 每个样本的每个特征值除以该样本各个特征值绝对值的总和
row/=abs(row).sum()
# axis:轴向,axis=1:按行运算
print(abs(samples).sum(axis=1))
samples
2.4 二值化
有些业务并不需要分析矩阵的详细完整数据(比如图像边缘识别只需要分析出图像边缘即可),可以根据一个事先给定的阈值,用0和1表示特征值不高于或高于阈值。二值化后的数组中每个元素非0即1,达到简化数学模型的目的
二值化相关API:
# 给定阈值,获取二值化器
bin=sp.Binarizer(threshold=阈值)
# 调用transform方法对原始样本矩阵进行二值化预处理操作
result=bin.transform(原始样本矩阵)
案例:
import numpy as np
# 数据预处理库
import sklearn.preprocessing as sp
samples=np.array([
[10,21,5],
[2,4,1],
[11,18,18]])
# 方式1:
# 二值化
bin=sp.Binarizer(threshold=10)
result=bin.transform(samples)
print(result)
# 方式2:
# 复制数据
new_samples=samples.copy()
new_samples[new_samples<=10]=0
new_samples[new_samples>10]=1
new_samples
案例:
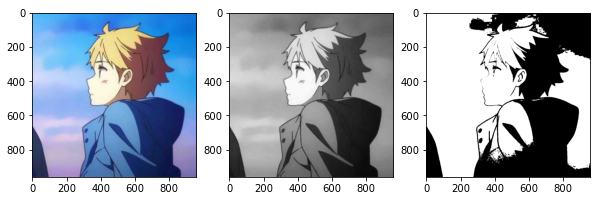
# 二值化图片
import matplotlib.pyplot as plt
# 数据预处理库
import sklearn.preprocessing as sp
from skimage import io
from skimage.color import rgb2gray
# 读取原始RGB图
img=io.imread("picture/pic.jpg")
# rgb2gray:原始RGB图转为灰度图
gray_img=rgb2gray(img)
print(gray_img)
# 给定阈值,获取二值化器
bin_img=sp.Binarizer(threshold=0.5)
# 调用transform方法对灰度图进行二值化预处理操作
result_img=bin_img.transform(gray_img)
# cmap: 颜色图谱(colormap), 默认绘制为RGB颜色空间 cmap="gray":黑-白颜色
plt.figure(figsize=(10,6))
# 原始RGB图
plt.subplot(1,3,1)
plt.imshow(img)
# 灰度图
plt.subplot(1,3,2)
plt.imshow(gray_img,cmap="gray")
# 二值化图
plt.subplot(1,3,3)
plt.imshow(result_img,cmap="gray")
plt.show()
2.5 独热编码(One-Hot Encoding)
独热编码:为样本特征的每个值建立一个由一个1和若干个0组成的序列,用该序列对所有的特征值进行编码
过程:
# 观察每列不同的数字,取每列不同的数字的个数=位数进行独热编码
# 4个样本(行)3个特征(列)
# 每列
# 两个不同的数 三个不同的数 四个不同的数
1 3 2
7 5 4
1 8 6
7 3 9
# 为每列的不同数字进行独热编码:
1——10 3——100 2——1000
7——01 5——010 4——0100
8——001 6——0010
9——0001
# 编码完毕后得到最终经过独热编码后的样本矩阵:
101001000
010100100
100010010
011000001
使用场景:计算相似度
独热编码相关API:
# 方式1:
import sklearn.preprocessing as sp
# 创建一个独热编码器
# sparse:是否使用紧缩格式(稀疏矩阵)
# dtype:数据类型
ohe=sp.OneHotEncoder(sparse=是否采用紧缩格式,dtype=数据类型)
# 对原始样本矩阵进行处理,返回独热编码后的样本矩阵
result=ohe.fit_transform(原始样本矩阵)
# 方式2:
import sklearn.preprocessing as sp
# 创建一个独热编码器
# sparse:是否使用紧缩格式(稀疏矩阵)
# dtype:数据类型
ohe=sp.OneHotEncoder(sparse=是否采用紧缩格式,dtype=数据类型)
# 对原始样本矩阵进行训练,得到编码字典
encode_dict=ohe.fit(原始样本矩阵)
# 调用encode_dict字典的transform方法对数据样本矩阵进行独热编码
result=encode_dict.transform(原始样本矩阵)
案例:
import numpy as np
# 数据预处理库
import sklearn.preprocessing as sp
samples=np.array([
[1,3,2],
[7,5,4],
[1,8,6],
[7,3,9]])
# 独热编码
# 方式1:
# 创建一个独热编码器
# sparse:是否使用紧缩格式(稀疏矩阵)
# dtype:数据类型
ohe=sp.OneHotEncoder(sparse=False,dtype="int32")
# 对原始样本矩阵进行处理,返回独热编码后的样本矩阵
result=ohe.fit_transform(samples)
print(result,type(result))
# 方式2:
# 创建一个独热编码器
# sparse:是否使用紧缩格式(稀疏矩阵)
# dtype:数据类型
ohe=sp.OneHotEncoder(sparse=False,dtype="int32")
# 对原始样本矩阵进行训练,得到编码字典
encode_dict=ohe.fit(samples)
# 调用encode_dict字典的transform方法对数据样本矩阵进行独热编码
new_result=encode_dict.transform(samples)
print(new_result,type(new_result))
2.6 标签编码
标签编码:根据字符串形式的特征值在特征序列中的位置,为其指定一个数字标签,用于提供给基于数值算法的学习模型
标签编码相关API:
import sklearn.preprocessing as sp
# 获取标签编码器
lbe=sp.LabelEncoder()
# 调用标签编码器的fit_transform方法训练并且为原始样本特征数组(一维数组:列)进行标签编码
result=lbe.fit_transform(原始样本特征数组)
# 根据标签编码的结果矩阵反查字典,解码得到原始数据矩阵
samples=lbe.inverse_transform(result)
案例:
import numpy as np
# 数据预处理库
import sklearn.preprocessing as sp
samples=np.array(["audi","ford","audi","toyota","ford","bmw","toyota","ford","audi"])
# 获取标签编码器
lbe=sp.LabelEncoder()
# 调用标签编码器的fit_transform方法训练并且为原始样本特征数组(一维数组:列)进行标签编码
result=lbe.fit_transform(samples)
print(result)
# 根据标签编码的结果矩阵反查字典,解码得到原始数据矩阵
samples=lbe.inverse_transform(result)
print(samples)
# 假设训练之后得到一组测试样本的结果:
test=[0,0,2,3,1]
print(lbe.inverse_transform(test))
