附录C 卷积案例
卷积常用于图像神经网络中,既可以作为分类器,也可以作为生成器。在设计卷积神经网络时,我们需要清楚每个卷积层输出数据的形状。
在本附录中,我们将通过常用的卷积层配置,了解如何得出这些数据的形状。
特别需要注意的是,转置卷积普遍被认为是较难掌握的。这里,我们将通过一些例子来证明它们并不难理解。这些例子都遵循了一个非常简单的窍门。
C.1 例1: 卷积,步长为1,无补全
在第1个例子中,输入图像大小为6×6,我们使用一个2×2的卷积核,步长为1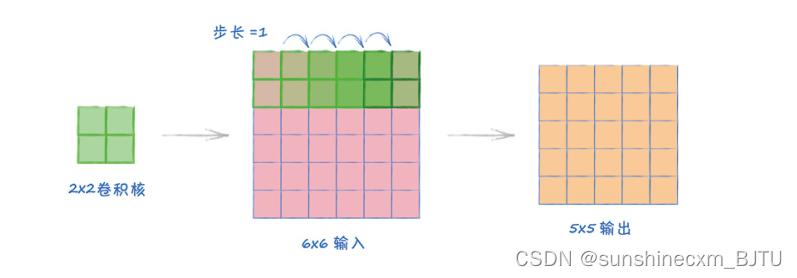
上图显示了卷积核是如何沿着图像以步长1移动的。卷积核覆盖的区域有重叠,但这并不是问题。
图像从左到右,卷积核可以占5个位置,这是输出的宽度是5的原因。从上到下,卷积核也可以占5个位置,这就是输出是一个5×5的正方形图像的原因。很容易吧!
实现这个例子的PyTorch代码为:
nn.Conv2d(in_channels, out_channels, kernel_size=2, stride=1)
C.2 例2: 卷积,步长为2,无补全
第2个例子与第1个例子基本相同,唯一的区别是,现在步长为2。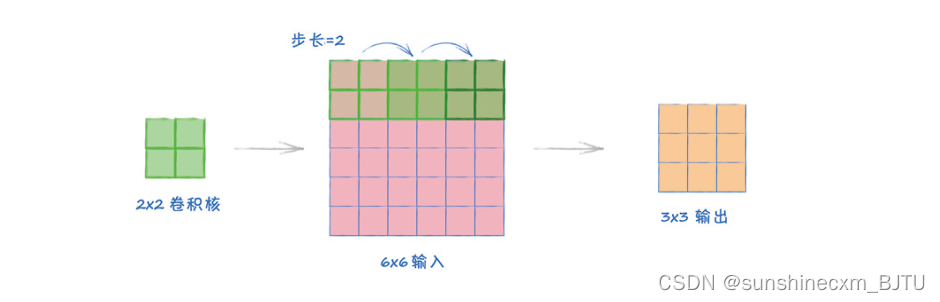
上图显示了卷积核是如何沿着图像以步长2移动的。
这次,卷积核覆盖的区域没有重叠。事实上,由于卷积核的大小与步长相等,图像可以被无缝覆盖。卷积核可以在图像上横着或竖着走3个位置,因此输出大小是3×3。
实现这个例子的PyTorch代码为:
nn.Conv2d(in_channels, out_channels, kernel_size=2, stride=2)
C.3 例3: 卷积,步长为2,有补全
第3个例子与第2个例子一样,不过现在我们加入补全。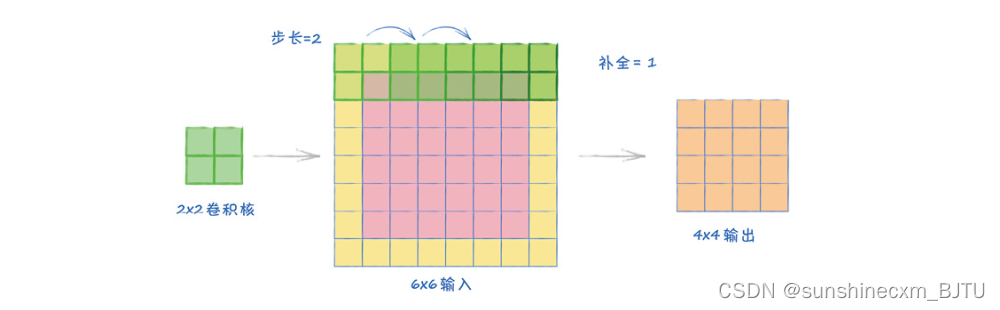
通过设置补全为1,我们将所有的图像边缘都扩展了1个像素,像素值为0。这意味着图像的宽度增加了2个像素。我们将卷积核应用于这个扩展后的图像上。
从上图可见,卷积核可以在整个图像上占据4个位置。这就是为什么输出大小是4×4。
实现这个例子的PyTorch代码为:
nn.Conv2d(in_channels, out_channels, kernel_size=2, stride=2, padding=2)
C.4 例4: 卷积,不完全覆盖
在这个例子中,卷积核的大小和步长决定了它无法覆盖图像的边缘。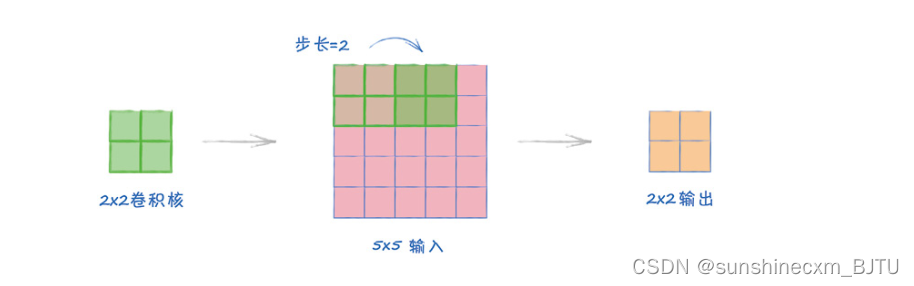
这里,2×2的卷积核在5×5的图像上以步长2移动。图像的最后一列没有被覆盖。
最简单的解决方法是直接忽略未覆盖的列。事实上,包括PyTorch在内的许多工具都是这样做的。这也是输出大小是2×2的原因。
对于较大的图像,丢失图像最边缘的信息问题不大,因为有意义的内容通常在图像的中间位置。即使不在,丢失的信息也是小部分的。
如果真的希望避免丢失任何信息,我们需要调整一些选项。比如,我们可以通过添加补全,确保不遗漏输入图像的任何部分。或者,我们可以调整卷积核和步长的大小,使其与图像大小相匹配。
C.5 例5: 转置卷积,步长为2,无补全
转置卷积通常被用于将一个张量扩展为较大的张量。它与普通卷积相反,卷积将一个张量缩减成一个较小的张量。在这个例子中,我们同样使用一个2×2的卷积核,以步长2扩展一个3×3的输入。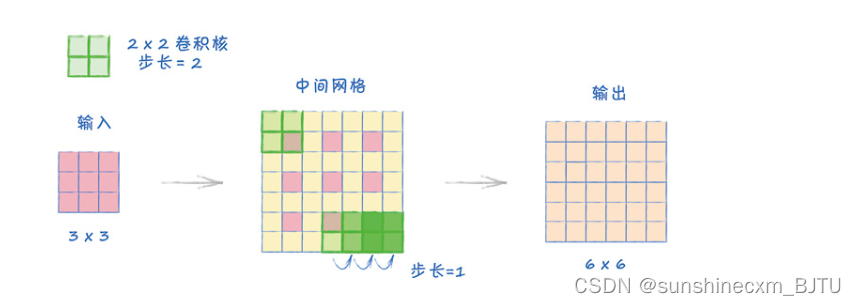
转置卷积的过程中有一些额外的步骤,但是都不复杂。
首先,我们创建一个中间网格,将原始输入的方格按步长间隔开。在上图中,粉红色的方格以步长2间隔开。中间新加入的方格的值等于0。
其次,我们用0值扩展图像的边缘方格。原输入的四周全部被扩展。扩展后,卷积核在左上角可以覆盖一个粉红色方格,如上图中的中间网格所示。如果我们在四周再扩展一圈方格,卷积核就无法覆盖原来的粉红色方格。
最后,卷积核在这个中间网格上以步长1移动。这个步长是固定的。不同于一般的卷积,这里的步长选项不用来决定卷积核的移动方式,而只用于设置原始方格在中间网格中的距离。
卷积核在这个7×7的中间网格上移动,输出的结果是一个6×6的网格。
注意转置卷积如何将3×3的输入转换成6×6的输出。整个过程与例2正好相反。例2使用相同大小的卷积核和步长,将一个6×6的输入转换成3×3的输出。
实现这个例子的PyTorch代码为:
nn.ConvTranspose2d(in_channels, out_channels, kernel_size=2, stride=2)
C.6 例6: 转置卷积,步长为1,无补全
在第5个例子中,为了简单演示它的工作原理,我们将步长设为2。在本例中,我们将步长设为1。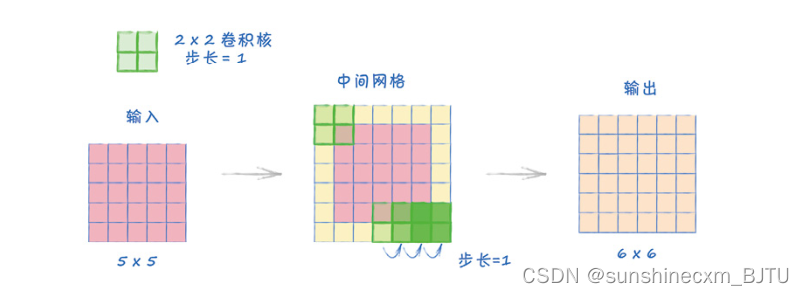
整个过程与之前完全相同。由于跨度是1,因此在中间网格中的原始方格的间隔是1,即没有空隙。接着,我们使用附加外环来扩展中间网格,使卷积核在左上角仍然可以覆盖到一个原始方格。然后,我们用卷积核以步长为1在这个7×7的中间网格上移动,最后得到一个6×6的输出。
整个过程与例1相反。
实现这个例子的PyTorch代码为:
nn.ConvTranspose2d(in_channels, out_channels, kernel_size=2, stride=1)
C.7 例7: 转置卷积,步长为2,有补全
在这个转置卷积的例子中,我们加入补全。与普通的卷积不同,之前补全的作用是扩展图像。在这里,补全的作用是缩小图像。
我们有一个2×2的卷积核,步长设为2,输入大小为3×3,补全设为1。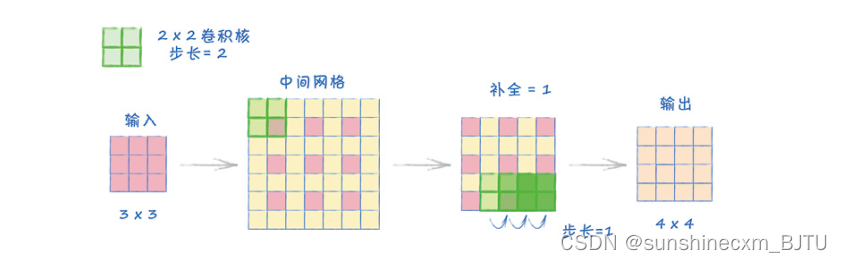
首先,与例5一样,我们创建中间网格。接着,我们将原始方格的间距设为2,并扩展网格四周,使卷积核可以覆盖其中一个原始值。
因为补全被设为1,所以我们从网格周围去掉1个环。再将卷积核应用到这个网格中,得到了一个4×4的输出。
实现这个例子的PyTorch代码为:
nn.ConvTranspose2d(in_channels, out_channels, kernel_size=2, stride=2, padding=1)
C.8 计算输出大小
假设输入是一个正方形,宽度和高度相等。那么,计算卷积输出大小的公式是:
L形括号的意义是取括号内数值的数学下限(floor),也就是一个小于或等于给定值的最大整数。例如,2.3的下限是2。
如果我们用这个公式计算例3的输出大小,则输入大小=6,补全=1,卷积核大小=2。L形括号内的计算是(6+2?1?1)/2+1,结果是4。4的下限是4,也就是输出的大小。
同样,假设输出是方形张量,则计算转置卷积输出大小的公式是:
让我们试着计算例7,输入大小=3,步长=2,补全=1,卷积核大小=2。计算结果是2×2 ? 2 + 1 + 1 = 4,所以输出的大小是4。
在以下PyTorch的参考页面中,我们可以阅读更多可以应用于矩形张量的通用公式以及一些额外的设置选项,我们在这里就不一一介绍了。
nn.Conv2d https://pytorch.org/docs/stable/nn.html#conv2d
nn.ConvTranspose2d https://pytorch.org/docs/stable/nn.html#convtranspose2d
