[人工智能]三种激活函数——SigmoidTanh ReLU以及卷积感受野的计算

1. 三种激活函数——Sigmoid, Tanh, ReLU

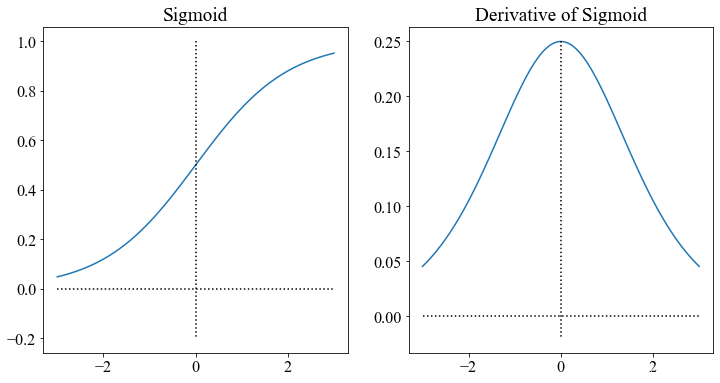
1.1 Sigmoid

1.1.1 公式

$$S(x)=\frac{1}{1+e^{?x}}$$

1.1.2 导数

$$S^{\prime }(x)=\frac{e^{?x}}{(1+e^{?x}{)}^2}=S(x)(1?S(x))$$

1.1.3 函数图像

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import rcParams


plt.figure(figsize=(12, 6))
config = {
    "font.family": 'Times New Roman',
    "font.size": 16,
    "mathtext.fontset": 'stix',
    "font.serif": ['Times New Roman'],
}
rcParams.update(config)

# Sigmoid
plt.subplot(1, 2, 1)
x = np.linspace(-3, 3, 100)
sigmoid = 1 / (1 + np.exp(-x))
plt.plot(x, sigmoid, label="Sigmoid")
# 刻度线
plt.plot([0, 0], [1, -0.2], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Sigmoid")


# Sigmoid的导函数
plt.subplot(1, 2, 2)
x = np.linspace(-3, 3, 100)
sigmoid_div = sigmoid * (1 - sigmoid)
plt.plot(x, sigmoid_div, label="Derivative of Sigmoid")
# 刻度线
plt.plot([0, 0], [0.25, -0.02], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Derivative of Sigmoid")

1.1.4 优点

1. 实现简单，导数易获得。
2. 输出在[0,1]，所以可以用作输出层，表示概率。
3. 最大熵模型，受噪声数据影响较小：

1.1.5 缺点

1. 梯度饱和：指在sigmoid函数曲线的两段，(x>>0或x<<0)时，梯度接近0，从而在层级神经网络结构中，导致训练缓慢，以及梯度消失现象。

1.2 Tanh

Tanh的诞生比Sigmoid晚一些，Sigmoid函数我们提到过有一个缺点就是输出不以0为中心，使得收敛变慢的问题。而Tanh则就是解决了这个问题。

1.2.1 公式

$$\tanh (x)=\frac{\sinh (x)}{\cosh (x)}=\frac{e^x?e^{?x}}{e^x+e^{?x}}$$

1.2.2 导数

$${\tanh }^{\prime }(x)=1?{\tanh }^2(x)$$

1.2.3 函数图像

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import rcParams


plt.figure(figsize=(12, 6))
config = {
    "font.family": 'Times New Roman',
    "font.size": 16,
    "mathtext.fontset": 'stix',
    "font.serif": ['Times New Roman'],
}
rcParams.update(config)

# Tanh
plt.subplot(1, 2, 1)
x = np.linspace(-3, 3, 100)
tanh = (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
plt.plot(x, tanh)
# 刻度线
plt.plot([0, 0], [1, -1], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Tanh")


# Tanh的导函数
plt.subplot(1, 2, 2)
x = np.linspace(-3, 3, 100)
tanh_div = 1 - tanh**2
plt.plot(x, tanh_div, label="Derivative of Tanh")
# 刻度线
plt.plot([0, 0], [1.1, -0.02], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Derivative of Tanh")

1.2.4 优点

1. 解决了sigmoid函数收敛变慢的问题，相对于sigmoid提高了收敛速度。
2. 因为Tanh和Sigmoid的导函数有上下界，所以完全不用担心因为使用激活函数而产生梯度爆炸的问题

1.2.5 缺点

1. 指数的计算复杂。
2. 梯度消失的问题依旧保留，因为两边的饱和性使得梯度消失，进而难以训练。

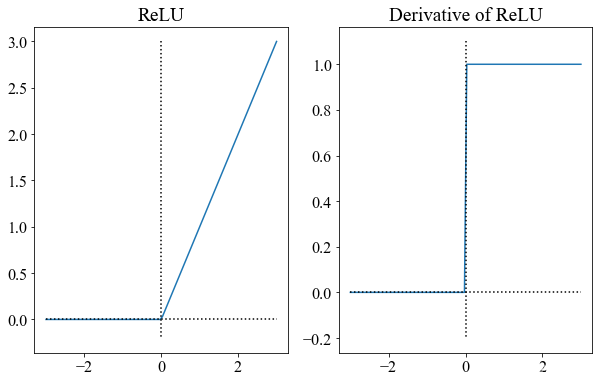
1.3 ReLU

1.3.1 公式

$$\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}(x)=\{\begin{array}{ll}x,& x\ge 0\\ 0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}$$

1.3.2 导数

$$\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}(x)=\{\begin{array}{ll}1,& x\ge 0\\ 0,& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}$$

1.3.3 函数图像

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import rcParams


plt.figure(figsize=(10, 6))
config = {
    "font.family": 'Times New Roman',
    "font.size": 16,
    "mathtext.fontset": 'stix',
    "font.serif": ['Times New Roman'],
}
rcParams.update(config)

# ReLU
plt.subplot(1, 2, 1)
x = np.linspace(-3, 3, 100)
ReLU = np.maximum(0, x)
plt.plot(x, ReLU)
# 刻度线
plt.plot([0, 0], [3, -0.2], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("ReLU")


# ReLU的导函数
plt.subplot(1, 2, 2)
x = np.linspace(-3, 3, 100)
ReLU_div = [1 if value >= 0 else 0 for value in x]
plt.plot(x, ReLU_div, label="Derivative of ReLU")
# 刻度线
plt.plot([0, 0], [1.1, -0.2], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Derivative of ReLU")

1.3.4 优点

1. 没有饱和区，不存在梯度消失问题，防止梯度弥散；
2. 稀疏性；
3. 没有复杂的指数运算，计算简单、效率提高；
4. 实际收敛速度较快，比 Sigmoid/tanh 快很多；
5. 比 Sigmoid 更符合生物学神经激活机制。

1.3.5 缺点

就是训练的时候很”脆弱”，很容易就”die”了。

举个例子：一个非常大的梯度流过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了。如果这个情况发生了，那么这个神经元的梯度就永远都会是0。

实际操作中，如果你的learning rate 很大，那么很有可能你网络中的40%的神经元都”dead”了。 当然，如果你设置了一个合适的较小的learning rate，这个问题发生的情况其实也不会太频繁。

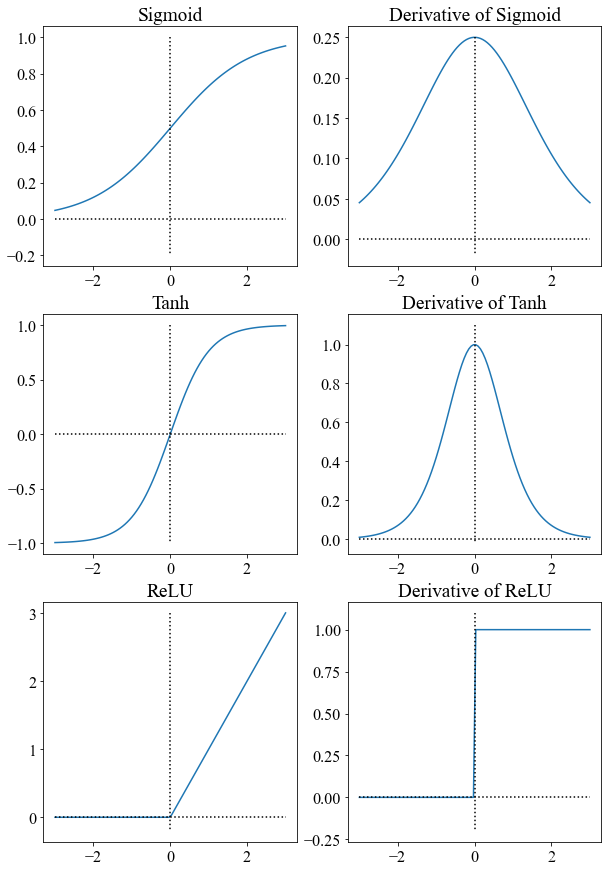
1.4 三种激活函数的图像

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import rcParams


plt.figure(figsize=(10, 15))
config = {
    "font.family": 'Times New Roman',
    "font.size": 16,
    "mathtext.fontset": 'stix',
    "font.serif": ['Times New Roman'],
}
rcParams.update(config)

# Sigmoid
plt.subplot(3, 2, 1)
x = np.linspace(-3, 3, 100)
sigmoid = 1 / (1 + np.exp(-x))
plt.plot(x, sigmoid, label="Sigmoid")
# 刻度线
plt.plot([0, 0], [1, -0.2], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Sigmoid")


# Sigmoid的导函数
plt.subplot(3, 2, 2)
x = np.linspace(-3, 3, 100)
sigmoid_div = sigmoid * (1 - sigmoid)
plt.plot(x, sigmoid_div, label="Derivative of Sigmoid")
# 刻度线
plt.plot([0, 0], [0.25, -0.02], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Derivative of Sigmoid")

# Tanh
plt.subplot(3, 2, 3)
x = np.linspace(-3, 3, 100)
tanh = (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
plt.plot(x, tanh)
# 刻度线
plt.plot([0, 0], [1, -1], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Tanh")


# Tanh的导函数
plt.subplot(3, 2, 4)
x = np.linspace(-3, 3, 100)
tanh_div = 1 - tanh**2
plt.plot(x, tanh_div, label="Derivative of Tanh")
# 刻度线
plt.plot([0, 0], [1.1, -0.02], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Derivative of Tanh")

# ReLU
plt.subplot(3, 2, 5)
x = np.linspace(-3, 3, 100)
ReLU = np.maximum(0, x)
plt.plot(x, ReLU)
# 刻度线
plt.plot([0, 0], [3, -0.2], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("ReLU")


# ReLU的导函数
plt.subplot(3, 2, 6)
x = np.linspace(-3, 3, 100)
ReLU_div = [1 if value >= 0 else 0 for value in x]
plt.plot(x, ReLU_div, label="Derivative of ReLU")
# 刻度线
plt.plot([0, 0], [1.1, -0.2], c="k", ls=":", lw=1.5)
plt.plot([-3, 3], [0, 0], c="k", ls=":", lw=1.5)
plt.title("Derivative of ReLU")

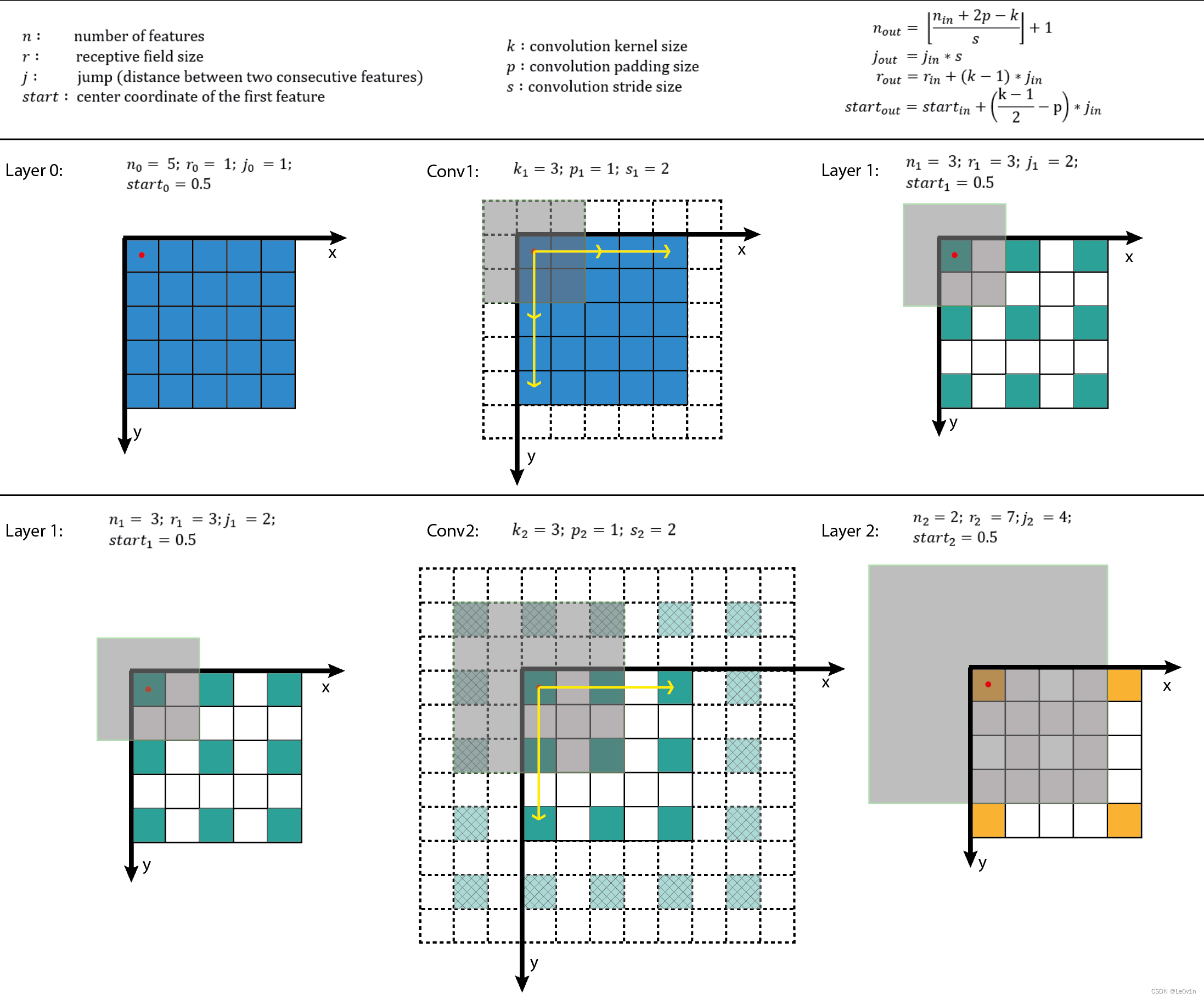
2. 卷积感受野计算

2.1 概念

感受野（Receptive Field），指的是神经网络中神经元“看到的”输入区域，在卷积神经网络中，feature map上某个元素的计算受输入图像上某个区域的影响，这个区域即该元素的感受野。

卷积神经网络中，越深层的神经元看到的输入区域越大，如下图所示，kernel size 均为3×3，stride均为1，绿色标记的是Layer2 每个神经元看到的区域，黄色标记的是Layer3 看到的区域，具体地，Layer2每个神经元可看到Layer1 上 3×3 大小的区域，Layer3 每个神经元看到Layer2 上 3×3 大小的区域，该区域可以又看到Layer1 上 5×5 大小的区域。

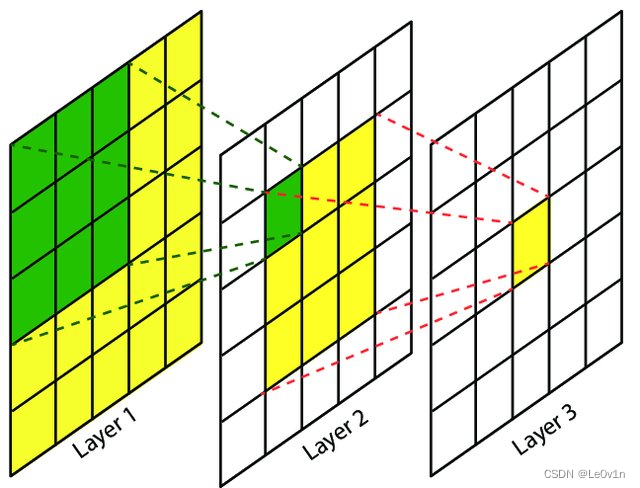
所以，感受野是个相对概念，某层feature map上的元素看到前面不同层上的区域范围是不同的，通常在不特殊指定的情况下，感受野指的是看到输入图像上的区域。

为了具体计算感受野，这里借鉴视觉系统中的概念，

$$\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{e}\mathrm{l}\mathrm{d}=\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}+\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}$$

准确计算感受野，需要回答两个问题，即视野中心在哪和视野范围多大。

• 只有看到“合适范围的信息”才可能做出正确的判断，否则就可能“盲人摸象”或者“一览众山小”；
• 目标识别问题中，我们需要知道神经元看到是哪个区域，才能合理推断物体在哪以及判断是什么物体。

但是，网络架构多种多样，每层的参数配置也不尽相同，感受野具体该怎么计算？

2.2 约定

在正式计算之前，先对数学符号做如下约定。

• $k$：kernel size

• $p$：padding size

• $s$：stride size

• $Layer$：用Layer表示feature map，特别地 $Laye{r}_0$ 为输入图像；

• $Conv$：用Conv表示卷积，$k、p、s$为卷积层的超参数，$Con{v}_l$的输入和输出分别为 $Laye{r}_{l?1}$ 和 $Laye{r}_l$；

• $n$：feature map size为 $n\times n$，这里假定$height=width$；

• $r$：receptive field size为$r\times r$，这里假定感受野为正方形；

• $j$：feature map上相邻元素间的像素距离，即将feature map上的元素与输入图像$Laye{r}_0$上感受野的中心对齐后，相邻元素在输入图像上的像素距离，也可以理解为 feature map上前进$1$步相当于输入图像上前进多少个像素，如下图所示，feature map上前进$1$步，相当于输入图像上前进$2$个像素，$j=2$；
  

• $start$：feature map左上角元素在输入图像上的感受野中心坐标$(start,start)$，即视野中心的坐标，在上图中，左上角绿色块感受野中心坐标为$(0.5,0.5)$，即左上角蓝色块中心的坐标，左上角白色虚线块中心的坐标为$(?0.5,?0.5)$；

• $l$：$l$表示层，卷积层为$Con{v}_l$，其输入feature map为$Laye{r}_{l?1}$，输出为$Laye{r}_l$。

下面假定所有层均为卷积层。

2.3 感受野大小

感受野大小的计算是个递推公式。

再看上面的动图，如果feature map $Laye{r}_2$ 上的一个元素$A$看到feature map $Laye{r}_1$ 上的范围为$3\times 3$（图中绿色块），其大小等于kernel size $k_2$，所以，$A$看到的感受野范围$r_2$等价于$Laye{r}_1$上$3\times 3$窗口看到的$Laye{r}_0$ 范围，据此可以建立起相邻$Layer$感受野的关系，如下所示，其中$r_l$为$Laye{r}_l$的感受野，$r_{l?1}$为$Laye{r}_{l?1}$ 的感受野，
$$r_l=r_{l?1}+(k_l?1)\times j_{l?1}$$

• $Laye{r}_l$：一个元素的感受野$r_l$等价于$Laye{r}_{l?1}$ 上$k\times k$ 个感受野的叠加；
• $Laye{r}_{l?1}$ 上一个元素的感受野为$r_{l?1}$；
• $Laye{r}_{l?1}$ 上连续$k$个元素的感受野可以看成是，第1个元素看到的感受野加上剩余$k?1$步扫过的范围，$Laye{r}_{l?1}$ 上每前进1个元素相当于在输入图像上前进$j_l?1$个像素，结果等于$r_l?1+(k?1)\times j_l?1$

可视化如下图所示，

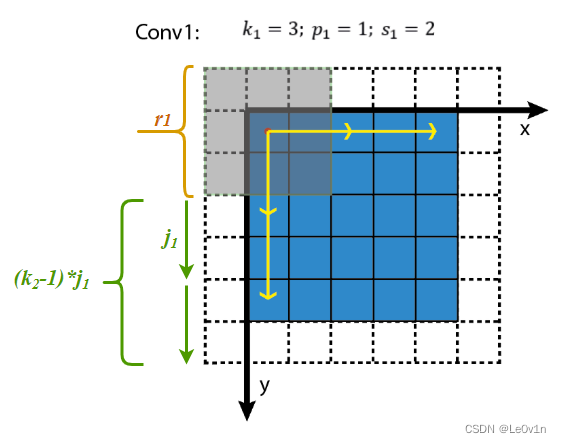
下面的问题是，$j_{in}$怎么求？

$Laye{r}_l$ 上前进1个元素相当于$Laye{r}_{l?1}$上前进$s_l$个元素，转换成像素单位为
$$j_l=j_{l?1}\times s_l$$
其中，$s_l$为Conv l的kernel在$Laye{r}_{l?1}$ 上滑动的步长，输入图像的$s_0=1$。

根据递推公式可知，
$$j_l=\prod _{i=1}^l{s}_i$$
$Laye{r}_l$上前进1个元素，相当于在输入图像前进了${\prod }_{i=1}^l$个像素，即前面所有层$stride$的连乘。

进一步可得，$Laye{r}_l$的感受野大小为

$$\begin{gathered} r_l=r_{l?1}+(k_l?1)?j_{l?1} \\ =r_{l?1}+((k_l?1)\times \prod _{i=1}^{l?1}{s}_i) \end{gathered}$$

2.4 感受野中心

感受野中心的计算也是个递推公式。

在上一节中计算得$j_l={\prod }_{i=1}^l{s}_i$，表示feature map $Laye{r}_l$上前进1个元素相当于在输入图像上前进的像素数目，如果将feature map上元素与感受野中心对齐，则$j_l$为感受野中心之间的像素距离。如下图所示，

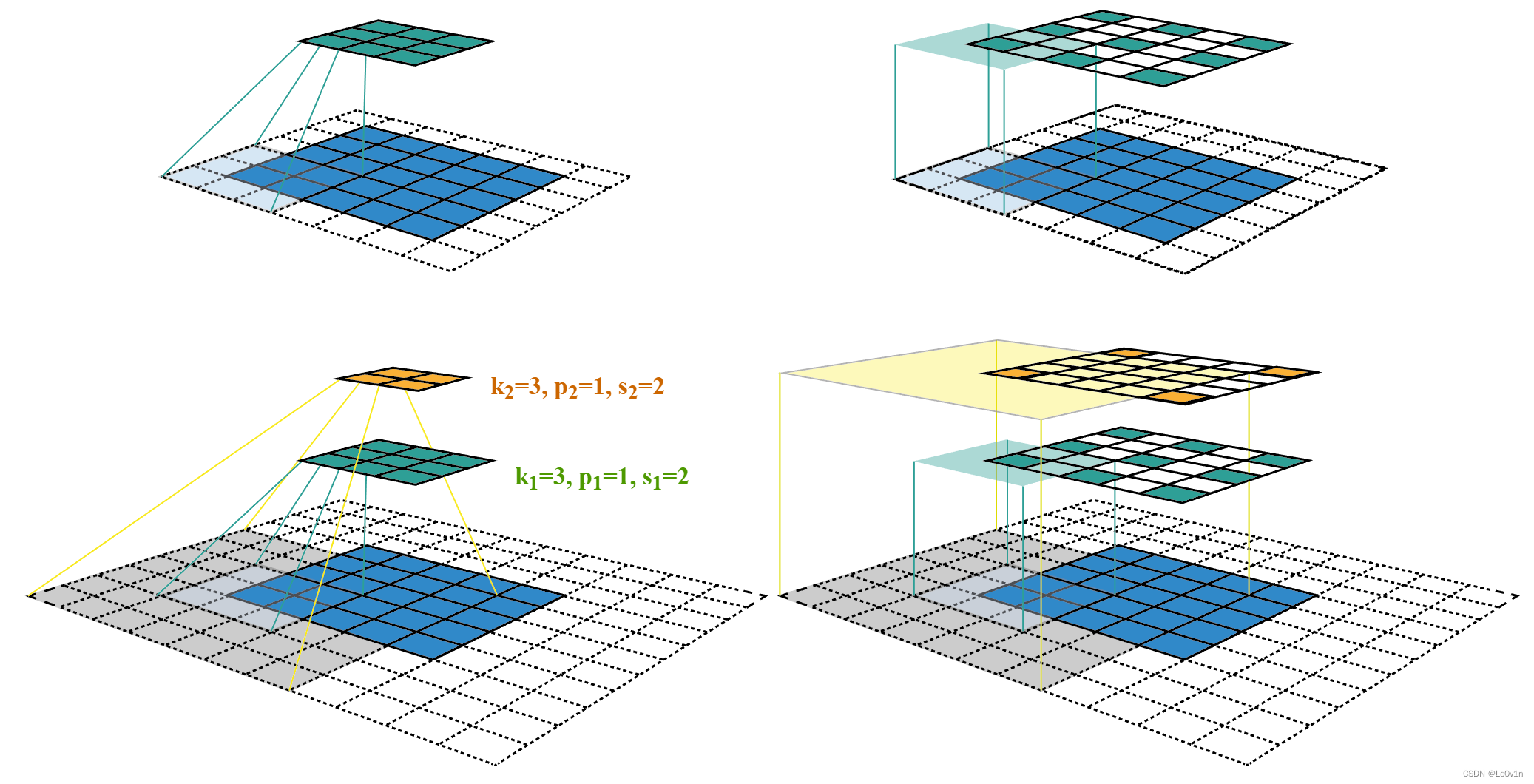
其中，各层的$kernelsize、padding、stride$超参数已在图中标出，右侧图为feature map和感受野中心对齐后的结果。

相邻$Layer$间，感受野中心的关系为

$$star{t}_l=star{t}_{l?1}+(\frac{k_l?1}{2}?p_l)\times j_{l?1}$$

所有的$start$坐标均相对于输入图像坐标系。其中，$star{t}_0=(0.5,0.5)$，为输入图像左上角像素的中心坐标，$star{t}_{l?1}$表示$Laye{r}_{l?1}$左上角元素的感受野中心坐标，$(\frac{k_l?1}{2}?p_l)$为$Laye{r}_l$与$Laye{r}_{l?1}$感受野中心相对于$Laye{r}_{l?1}$坐标系的偏差，该偏差需折算到输入图像坐标系，其值需要乘上$j_{l?1}$，即$Laye{r}_{l?1}$相邻元素间的像素距离，相乘的结果为$(\frac{k_l?1}{2}?p_l)\times j_{l?1}$，即感受野中心间的像素距离——相对输入图像坐标系。至此，相邻Layer间感受野中心坐标间的关系就不难得出了，这个过程可视化如下。

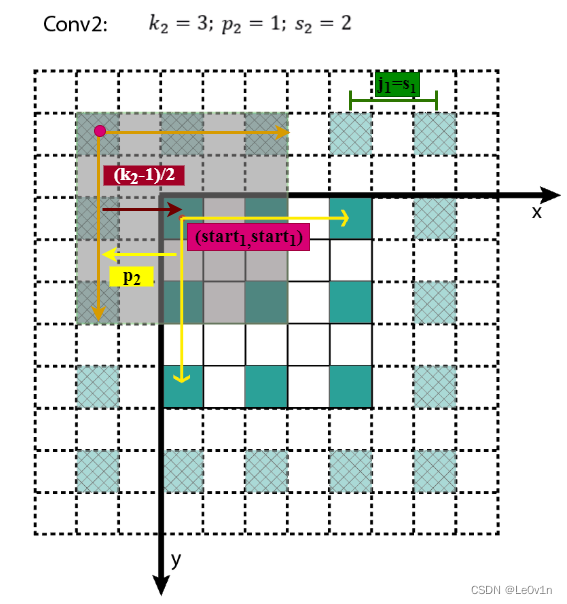
知道了$Laye{r}_l$左上角元素的感受野中心坐标$(star{t}_l,star{t}_l)$，通过该层相邻元素间的像素距离$j_l$可以推算其他元素的感受野中心坐标。

2.5 小结

将感受野的相关计算小结一下，
$$\begin{gathered} j_l=j_{l?1}\times s_l \\ {j}_l=\prod _{i=1}^l{s}_I \\ {r}_l=r_{l?1}+(k_l?1)\times j_{l?1} \\ =r_{l?1}+((k_l?1)\times \prod _{i=1}^{l?1}{s}_i) \\ star{t}_l=star{t}_{l?1}+(\frac{k_l?1}{2}?p_l)\times j_{l?1} \end{gathered}$$

由上面的递推公式，就可以从前向后逐层计算感受野了，代码可参见computeReceptiveField.py，在线可视化计算可参见Receptive Field Calculator。

最后，还有几点需要注意，

• $Laye{r}_l$的感受野大小与$s_l、p_l$无关，即当前feature map元素的感受野大小与该层相邻元素间的像素距离无关；
• 为了简化，通常将padding size设置为kernel的半径，即$p=\frac{k?1}{2}$，可得$star{t}_l=star{t}_{l?1}$，使得feature map $Laye{r}_l$ 上$(x,y)$位置的元素，其感受野中心坐标为$(x_{j_l},y_{j_l})$；
• 对于空洞卷积dilated convolution，相当于改变了卷积核的尺寸，若含有dilation rate参数，只需将$k_l$替换为$dilationrate\times (k_l?1)+1$，$dilationrate=1$时为正常卷积；
• 对于pooling层，可将其当成特殊的卷积层，同样存在kernel size、padding、stride参数；
• 非线性激活层为逐元素操作，不改变感受野。

2.6 代码计算感受野

# [filter size, stride, padding]
#Assume the two dimensions are the same
#Each kernel requires the following parameters:
# - k_i: kernel size
# - s_i: stride
# - p_i: padding (if padding is uneven, right padding will higher than left padding; "SAME" option in tensorflow)
# 
#Each layer i requires the following parameters to be fully represented: 
# - n_i: number of feature (data layer has n_1 = imagesize )
# - j_i: distance (projected to image pixel distance) between center of two adjacent features
# - r_i: receptive field of a feature in layer i
# - start_i: position of the first feature's receptive field in layer i (idx start from 0, negative means the center fall into padding)

import math
convnet =   [[11,4,0],[3,2,0],[5,1,2],[3,2,0],[3,1,1],[3,1,1],[3,1,1],[3,2,0],[6,1,0], [1, 1, 0]]
layer_names = ['conv1','pool1','conv2','pool2','conv3','conv4','conv5','pool5','fc6-conv', 'fc7-conv']
imsize = 227

def outFromIn(conv, layerIn):
  n_in = layerIn[0]
  j_in = layerIn[1]
  r_in = layerIn[2]
  start_in = layerIn[3]
  k = conv[0]
  s = conv[1]
  p = conv[2]
  
  n_out = math.floor((n_in - k + 2*p)/s) + 1
  actualP = (n_out-1)*s - n_in + k 
  pR = math.ceil(actualP/2)
  pL = math.floor(actualP/2)
  
  j_out = j_in * s
  r_out = r_in + (k - 1)*j_in
  start_out = start_in + ((k-1)/2 - pL)*j_in
  return n_out, j_out, r_out, start_out
  
def printLayer(layer, layer_name):
  print(layer_name + ":")
  print("\t n features: %s \n \t jump: %s \n \t receptive size: %s \t start: %s " % (layer[0], layer[1], layer[2], layer[3]))
 
layerInfos = []
if __name__ == '__main__':
#first layer is the data layer (image) with n_0 = image size; j_0 = 1; r_0 = 1; and start_0 = 0.5
  print ("-------Net summary------")
  currentLayer = [imsize, 1, 1, 0.5]
  printLayer(currentLayer, "input image")
  for i in range(len(convnet)):
    currentLayer = outFromIn(convnet[i], currentLayer)
    layerInfos.append(currentLayer)
    printLayer(currentLayer, layer_names[i])
  print ("------------------------")
  layer_name = raw_input ("Layer name where the feature in: ")
  layer_idx = layer_names.index(layer_name)
  idx_x = int(raw_input ("index of the feature in x dimension (from 0)"))
  idx_y = int(raw_input ("index of the feature in y dimension (from 0)"))
  
  n = layerInfos[layer_idx][0]
  j = layerInfos[layer_idx][1]
  r = layerInfos[layer_idx][2]
  start = layerInfos[layer_idx][3]
  assert(idx_x < n)
  assert(idx_y < n)
  
  print ("receptive field: (%s, %s)" % (r, r))
  print ("center: (%s, %s)" % (start+idx_x*j, start+idx_y*j))

2.7 计算题

题目：在CNN网络中，一张图经过核为$3\times 3$，步长为2的卷积层，ReLU激活函数层，BN层，以及一个步长为2，核为$2\times 2$的池化层后，再经过一个$3\times 3$的的卷积层，步长为1，此时的感受野是多少？

$$\begin{array}{rl}{r}_l& =r_{l?1}+(k_l?1)\times j_{l?1}\\ & =r_{l?1}+((k_l?1)\times \prod _{i=1}^{l?1}{s}_i)\end{array}$$

$$\begin{array}{rlr}& L_0=1& ：输入默认为1\\ & L_1=1+(3?1)\times \prod _{i=1}^{l?1}{s}_i=1+(3?1)\times 1=3& ：1（输入）+（本层卷积核大小?1）\times 之前层步长连乘（输入默认为1）\\ & L_2=3+(2?1)\times \prod _{i=1}^{l?1}{s}_i=3+(2?1)\times 2=5& ：3（上一层感受野）+（本层卷积核大小?1）\times 之前层步长连乘（1\times 2）\\ & L_3=5+(3?1)\times \prod _{i=1}^{l?1}{s}_i=5+(3?1)\times (2\times 2)=13& ：5（上一层感受野）+（本层卷积核大小?1）\times 之前层步长连乘（1\times 2\times 2）\end{array}$$

• 对于pooling层，可将其当成特殊的卷积层，同样存在kernel size、padding、stride参数
• 非线性激活层为逐元素操作，不改变感受野

故此时的感受野大小为13。

参考

1. https://www.cnblogs.com/shine-lee/p/12069176.html

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖