WGAN,WGAN-GP
原理
GAN有多种解释,这里我总结一下:
原始论文解读
https://zhuanlan.zhihu.com/p/25071913
(苏神专场)
互怼的艺术:从零直达WGAN-GP
https://spaces.ac.cn/archives/4439
从Wasserstein距离、对偶理论到WGAN
https://spaces.ac.cn/archives/6280
动力学角度
https://spaces.ac.cn/archives/6583
能量视角下的GAN模型
https://kexue.fm/archives/6316
https://kexue.fm/archives/6331
https://kexue.fm/archives/6612
几何角度
A Geometric View of Optimal Transportation and Generative Model ,https://arxiv.org/abs/1710.05488

我之前尝试着看懂这篇论文,发现需要懂最优传输理论。
然后我就找了一些最优传输的资料(感兴趣的可以在公众号后台回复CHSH获取):

(Computational Optimal Transport 这本书华东师范大学的王祥丰老师正在翻译。https://zhuanlan.zhihu.com/p/499401130)
又发现没有学过测度论很难读懂。( 限制人学习自由的永远是数学,划线以下是另一个境界:

)
不过,我找到了一篇不用测度论解析的论文(工科生狂喜):
https://sci-hub.st/10.1109/msp.2017.2695801


看完能大概知道最优传输是干什么的,以及这个理论的奠基者蒙日(Monge)和康托罗维奇(Kantorovich)做了什么。
Pytorch实现:生成正态分布数据
理论很难,实现倒是不难。
WGAN

图片来源:[1]
import numpy as np
from matplotlib import pyplot as plt
import matplotlib
import torch
import torch.nn as nn
import torch.optim as optim
torch.manual_seed(1)
np.random.seed(1)
matplotlib.rcParams['font.family'] = 'SimHei'
matplotlib.rcParams['axes.unicode_minus'] = False
plt.rcParams['figure.dpi'] = 150
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.model = nn.Sequential(
nn.Linear(16, 128),
nn.LeakyReLU(),
nn.Dropout(p=0.3),
nn.Linear(128, 256),
nn.LeakyReLU(),
nn.Dropout(p=0.3),
nn.Linear(256, 512)
)
def forward(self, inputs):
return self.model(inputs)
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(512, 256),
nn.Tanh(),
nn.Linear(256, 128),
nn.Tanh(),
nn.Linear(128, 1),
# nn.Sigmoid() # 去掉
)
def forward(self, inputs):
return self.model(inputs)
def normal_pdf(x, mu, sigma):
'''# 正态分布,概率密度函数'''
pdf = np.exp(-((x - mu) ** 2) / (2 * sigma ** 2)) / (sigma * np.sqrt(2 * np.pi))
return pdf
def draw(G, epoch, g_input_size):
'''画目标分布和生成分布'''
plt.clf()
# 画出目标分布
x = np.arange(-3, 9, 0.2)
y = normal_pdf(x, 3, 1)
plt.plot(x, y, 'r', linewidth=2)
# 画出生成的分布
test_data = torch.rand(1, g_input_size)
data = G(test_data).detach().numpy()
mean = data.mean()
std = data.std()
x = np.arange(np.floor(data.min()) - 5, np.ceil(data.max()) + 5, 0.2)
y = normal_pdf(x, mean, std)
plt.plot(x, y, 'orange', linewidth=2)
plt.hist(data.flatten(), bins=20, color='y', alpha=0.5, rwidth=0.9, density=True)
# 坐标图设置
plt.legend(['目标分布', '生成分布'])
plt.show()
plt.pause(0.1)
def train():
# 用于记录生成器生成的数据的均值和方差
G_mean = []
G_std = []
# 目标分布的均值和方差
data_mean = 3
data_std = 1
feature_num = 512
batch_size = 64
g_input_size = 16
epochs = 1001
d_epoch = 1 # 判别器的训练轮数
# 初始化网络
D = Discriminator()
G = Generator()
# 初始化优化器
d_learning_rate = 0.01
g_learning_rate = 0.001
# loss_func = nn.BCELoss()
optimiser_D = optim.RMSprop(D.parameters(), lr=d_learning_rate)
optimiser_G = optim.RMSprop(G.parameters(), lr=g_learning_rate)
clip_value = 0.01
plt.ion()
for epoch in range(epochs):
G.train()
# 1 训练判别器d_steps次
for _ in range(d_epoch):
# 1.1 真实数据real_data输入D,得到d_real
real_data = torch.tensor(np.random.normal(data_mean, data_std, (batch_size, feature_num)),
dtype=torch.float)
d_real = D(real_data)
# 1.2 生成数据的输出fake_data输入D,得到d_fake
g_input = torch.rand(batch_size, g_input_size)
fake_data = G(g_input).detach() # detach:只更新判别器的参数
d_fake = D(fake_data)
# 1.3 计算损失值,最大化EM距离
d_loss = -(d_real.mean() - d_fake.mean())
# 1.4 反向传播,优化
optimiser_D.zero_grad()
d_loss.backward()
optimiser_D.step()
# 1.5 截断
for p in D.parameters():
p.data.clamp_(-clip_value, clip_value)
# 2 训练生成器
# 2.1 G输入g_input,输出fake_data。fake_data输入D,得到d_g_fake
g_input = torch.rand(batch_size, g_input_size)
fake_data = G(g_input)
d_g_fake = D(fake_data)
# 2.2 计算损失值,最小化EM距离
g_loss = -d_g_fake.mean()
# 2.3 反向传播,优化
optimiser_G.zero_grad()
g_loss.backward()
optimiser_G.step()
# 2.4 记录生成器输出的均值和方差
G_mean.append(fake_data.mean().item())
G_std.append(fake_data.std().item())
if epoch % 10 == 0:
print("Epoch: {}, 生成数据的均值: {}, 生成数据的标准差: {}".format(epoch, G_mean[-1], G_std[-1]))
print('-' * 10)
G.eval()
draw(G, epoch, g_input_size)
plt.ioff()
plt.show()
plt.plot(G_mean)
plt.title('均值')
plt.savefig('wgan_mean')
plt.show()
plt.plot(G_std)
plt.title('标准差')
plt.savefig('wgan_std')
plt.show()
if __name__ == '__main__':
train()
WGAN-GP

图片来源[2]
import numpy as np
from matplotlib import pyplot as plt
import matplotlib
import torch
import torch.nn as nn
import torch.optim as optim
torch.manual_seed(1)
np.random.seed(1)
matplotlib.rcParams['font.family'] = 'SimHei'
matplotlib.rcParams['axes.unicode_minus'] = False
plt.rcParams['figure.dpi'] = 150
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.model = nn.Sequential(
nn.Linear(16, 128),
nn.LeakyReLU(),
nn.Dropout(p=0.3),
nn.Linear(128, 256),
nn.LeakyReLU(),
nn.Dropout(p=0.3),
nn.Linear(256, 512)
)
def forward(self, inputs):
return self.model(inputs)
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(512, 256),
nn.Tanh(),
nn.Linear(256, 128),
nn.Tanh(),
nn.Linear(128, 1),
)
def forward(self, inputs):
return self.model(inputs)
def cal_gradient_penalty(D, real, fake):
# 每一个样本对应一个sigma。样本个数为64,特征数为512:[64,512]
sigma = torch.rand(real.size(0), 1) # [64,1]
sigma = sigma.expand(real.size()) # [64, 512]
# 按公式计算x_hat
x_hat = sigma * real + (torch.tensor(1.) - sigma) * fake
x_hat.requires_grad = True
# 为得到梯度先计算y
d_x_hat = D(x_hat)
# 计算梯度,autograd.grad返回的是一个元组(梯度值,)
gradients = torch.autograd.grad(outputs=d_x_hat, inputs=x_hat,
grad_outputs=torch.ones(d_x_hat.size()),
create_graph=True, retain_graph=True, only_inputs=True)[0]
# 利用梯度计算出gradient penalty
gradient_penalty = ((gradients.norm(2, dim=1) - 1) ** 2).mean()
return gradient_penalty
def normal_pdf(x, mu, sigma):
'''正态分布的概率密度函数'''
pdf = np.exp(-((x - mu) ** 2) / (2 * sigma ** 2)) / (sigma * np.sqrt(2 * np.pi))
return pdf
def draw(G, epoch, g_input_size):
'''画目标分布和生成分布'''
plt.clf()
# 画出目标分布
x = np.arange(-3, 9, 0.2)
y = normal_pdf(x, 3, 1)
plt.plot(x, y, 'r', linewidth=2)
# 画出生成的分布
test_data = torch.rand(1, g_input_size)
data = G(test_data).detach().numpy()
mean = data.mean()
std = data.std()
x = np.arange(np.floor(data.min()) - 5, np.ceil(data.max()) + 5, 0.2)
y = normal_pdf(x, mean, std)
plt.plot(x, y, 'orange', linewidth=2)
plt.hist(data.flatten(), bins=20, color='y', alpha=0.5, rwidth=0.9, density=True)
# 坐标图设置
plt.legend(['目标分布', '生成分布'])
plt.show()
plt.pause(0.1)
def train():
G_mean = []
G_std = [] # 用于记录生成器生成的数据的均值和方差
data_mean = 3
data_std = 1 # 目标分布的均值和方差
batch_size = 64
g_input_size = 16
g_output_size = 512
epochs = 1001
d_epoch = 1 # 每个epoch判别器的训练轮数
# 初始化网络
D = Discriminator()
G = Generator()
# 初始化优化器
d_learning_rate = 0.01
g_learning_rate = 0.001
# loss_func = nn.BCELoss()
optimiser_D = optim.Adam(D.parameters(), lr=d_learning_rate)
optimiser_G = optim.Adam(G.parameters(), lr=g_learning_rate)
# clip_value = 0.01
plt.ion()
for epoch in range(epochs):
G.train()
# 1 训练判别器d_steps次
for _ in range(d_epoch):
# 1.1 真实数据real_data输入D,得到d_real
real_data = torch.tensor(np.random.normal(data_mean, data_std, (batch_size, g_output_size)),
dtype=torch.float)
d_real = D(real_data)
# 1.2 生成数据的输出fake_data输入D,得到d_fake
g_input = torch.rand(batch_size, g_input_size)
fake_data = G(g_input).detach() # detach:只更新判别器的参数
d_fake = D(fake_data)
# 1.3 计算损失值,最大化EM距离
d_loss = -(d_real.mean() - d_fake.mean())
gradient_penalty = cal_gradient_penalty(D, real_data, fake_data)
d_loss = d_loss + gradient_penalty * 0.5 # lambda=0.5,这个参数对效果影响很大
# 1.4 反向传播,优化
optimiser_D.zero_grad()
d_loss.backward()
optimiser_D.step()
# 2 训练生成器
# 2.1 G输入g_input,输出fake_data。fake_data输入D,得到d_g_fake
g_input = torch.rand(batch_size, g_input_size)
fake_data = G(g_input)
d_g_fake = D(fake_data)
# 2.2 计算损失值,最小化EM距离
g_loss = -d_g_fake.mean()
# 2.3 反向传播,优化
optimiser_G.zero_grad()
g_loss.backward()
optimiser_G.step()
# 2.4 记录生成器输出的均值和方差
G_mean.append(fake_data.mean().item())
G_std.append(fake_data.std().item())
if epoch % 10 == 0:
print("Epoch: {}, 生成数据的均值: {}, 生成数据的标准差: {}".format(epoch, G_mean[-1], G_std[-1]))
print('-' * 10)
G.eval()
draw(G, epoch, g_input_size)
plt.ioff()
plt.show()
plt.plot(G_mean)
plt.title('均值')
plt.show()
plt.plot(G_std)
plt.title('标准差')
plt.show()
if __name__ == '__main__':
train()
结果对比
| GAN | WGAN | WGAN-GP | |
|---|---|---|---|
| 均值 | 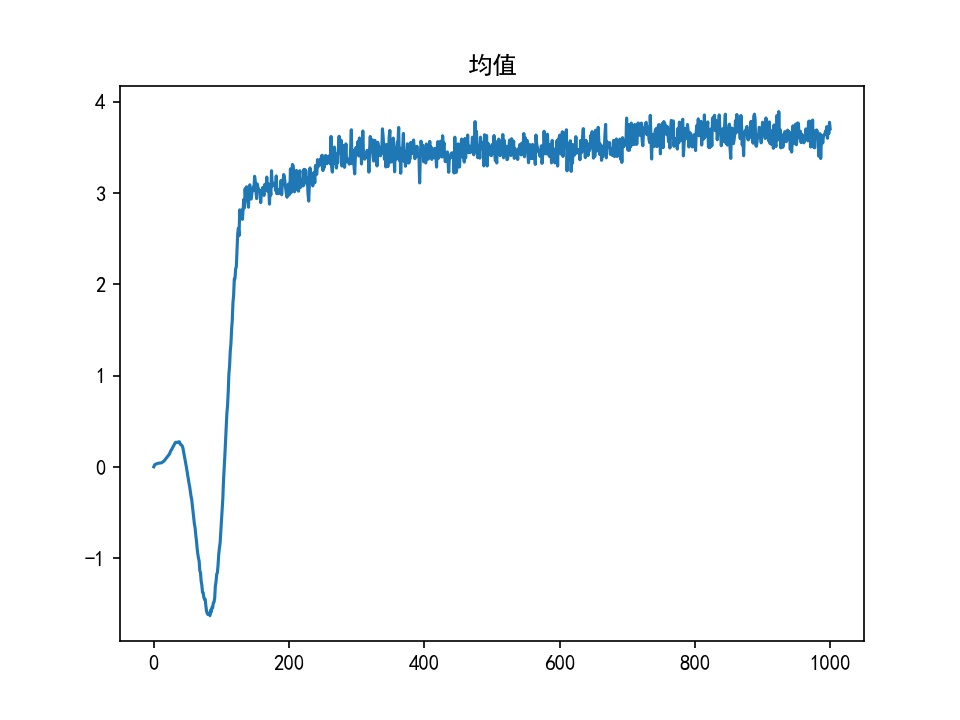 | 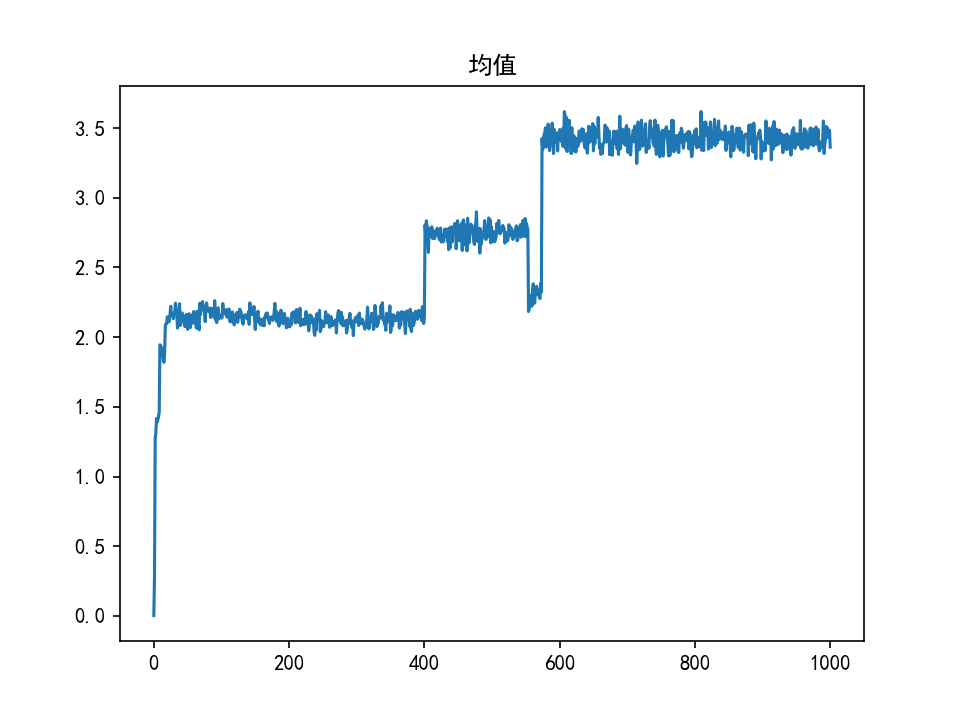 | 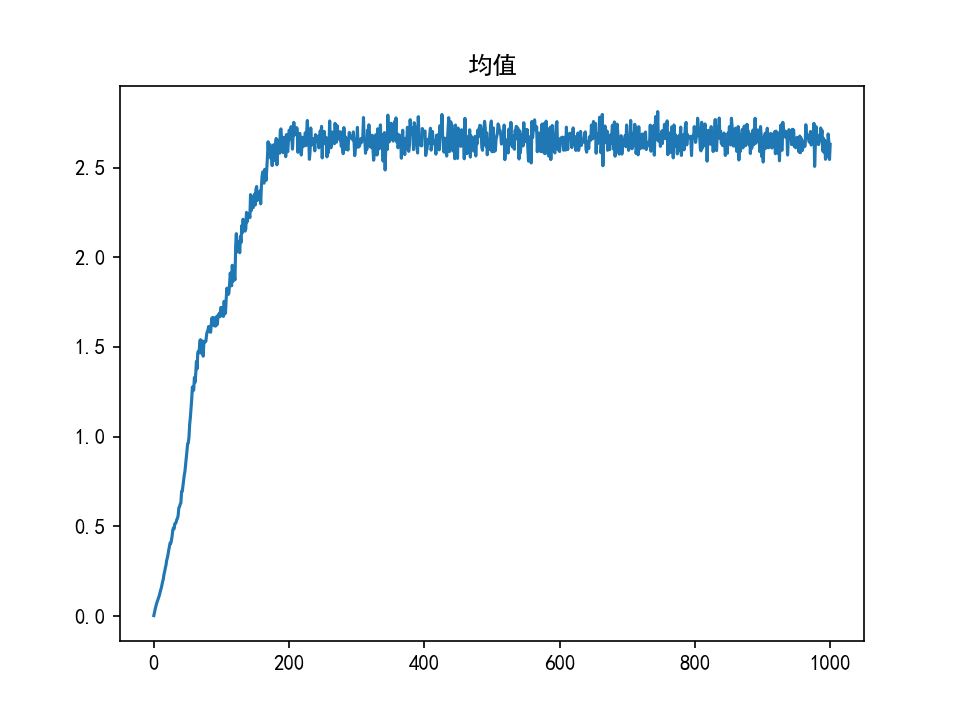 |
| 标准差 | 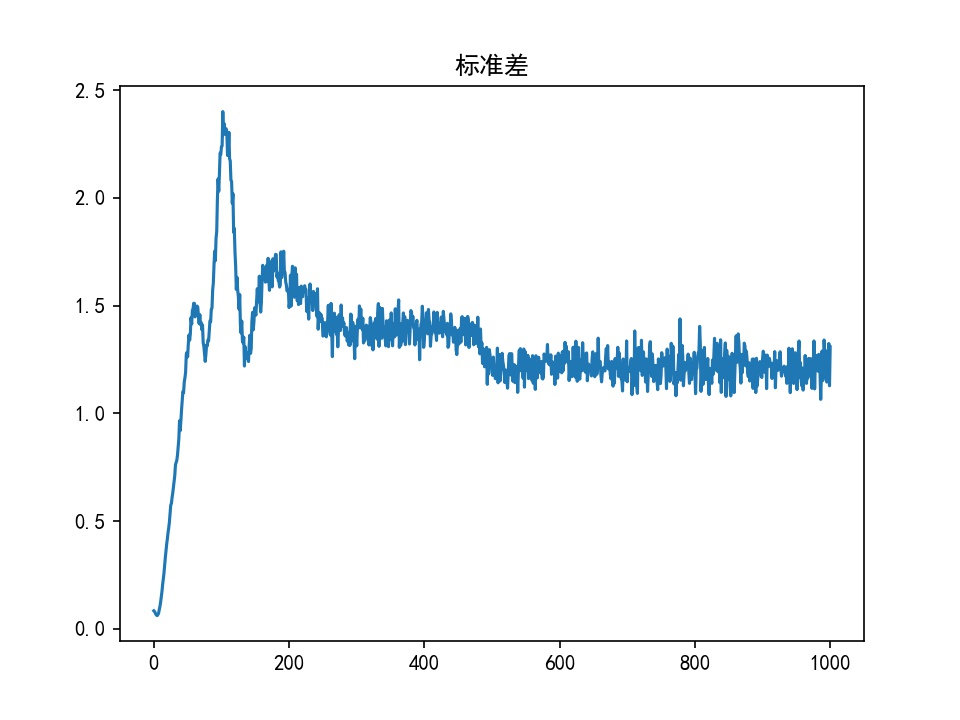 |  |  |
WGAN、WGAN-GP生成正态分布
[1] Wasserstein GAN, https://arxiv.org/abs/1701.07875
[2]Improved Training of Wasserstein GANs,https://arxiv.org/abs/1704.00028v3
