前言

在深度神经网络中，捕获long-range dependencies是至关重要的。对于序列数据，比如语音、文本，通常采用RNN对long-range dependency进行建模。对于图像数据，是通过堆叠卷积形成大的感受野来解决该问题的。?

CNN和RNN一次都只能处理一个局部邻域的信息，不管是在空间或是时间维度，因此只有不断重复操作，逐步传播信号才能捕获远程依赖关系。但是重复局部操作有一些局限，（1）计算效率低下（2）会导致优化困难（3）multihop dependency（即信息需要在长距离之间来回传递的情况）建模困难

本文提出了一种高效、简单、通用的组件来解决远程依赖关系的捕获问题，non-local operation。通过计算输入特征图中所有位置特征的加权和作为某一个位置的响应。这些位置的集和可以在空间、时间、时空中，这意味着我们的操作适用于图像、序列和视频。

non-local operation有以下几个优点：

与RNN和CNN的渐进方式不同，non-local操作通过计算任意两个位置之间的关系来直接捕获远程依赖关系，而不考虑它们的距离。
实验证明，non-local操作的效果更好，即使只在少数几层中使用也能得到最优的结果。
non-local操作保持了可变的输入大小，并且可以很容易地和其它操作结合起来，比如卷积。

Non-local Neural Networks

首先给出深度神经网络中non-local operation的一般表达

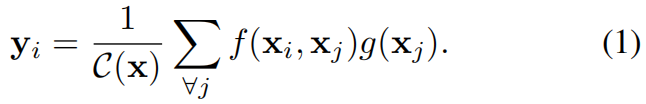
其中 \(i\) 是输出中一个位置的索引，其响应待计算，\(j\) 是待遍历的所有位置的索引。\(x\) 是输入信号（图像、序列、视频，通常是它们的特征），\(y\) 是与 \(x\) 大小相同的输出信号。函数 \(f\) 计算 \(i\) 和所有 \(j\) 之间的关系，输出一个标量。函数 \(g\) 计算输入信号位置 \(j\) 处的一个表示。最终通过 \(C(x)\) 进行归一化。?

实例化

接下来作者给出了函数 \(f\) 和 \(g\) 的几种不同选择，后续的实验表明最终的结果对 \(f\) 和 \(g\) 的具体函数形式并不敏感，这也表明了non-local operation其本身才是性能提升的主要原因。

为了简化过程，函数 \(g\)?只考虑linear embedding形式：\(g(x_{j})=W_{g}x_{j}\)，其中 \(W_{g}\)?是待学习的权重矩阵，这可以通过卷积实现，比如空间中的 \(1\times 1\) 卷积，时空中的 \(1\times 1\times 1\) 卷积。

对于 \(f\)?作者给出了多种选择：

Gaussian

高斯函数是一个很自然选择，这里?\(x^{T}_{i}x_{j}\)?通过点积衡量相似度，归一化因子设置为 \(C(x)=\sum_{\forall j}f(x_{i},x_{j})\)

Embedded Gaussian

高斯函数的一个简单的延伸就是在embedding空间中计算相似度，如下

这里 \(\theta(x_{i})=W_{\theta}x_{i}\)，\(\phi(x_{j})=W_{\phi}x_{j}\) 是两个embedding，这里设置 \(C(x)=\sum_{\forall j}f(x_{i},x_{j})\)。

self-attention module可以看作是embedded gaussian形式下non-local一种特殊情况，比如给定 \(i\)，\(\frac{1}{C(x)}f(x_{i},x_{j})\) 就是沿 \(j\)?维度的softmax函数。所以我们有 \(y=softmax(x^{T}W^{T}_{\theta}W_{\phi}x)g(x)\)，这就是self-attention原论文中的形式。

Dot product

这里设置 \(C(x)=N\)，?\(N\) 是 \(x\) 中位置的个数。dot product和embedded gaussian的差异就在于是否有softmax，softmax相当于激活函数。

Concatenation

这里 \([\cdot,\cdot]\)?表示concatenation，\(w_{f}\) 是一个权重向量将拼接后的vector映射为一个scalar。这里设置 \(C(x)=N\)

Non-local Block

作者将公式 (1) 中的non-local operation合并到一个non-local block中，然后可以方便的合并到现有的模型结构中。具体如下

其中 \(y_{i}\) 是式 (1) 的结果，\(+x_{i}\)?是残差连接，一个完整的non-local block如下图所示

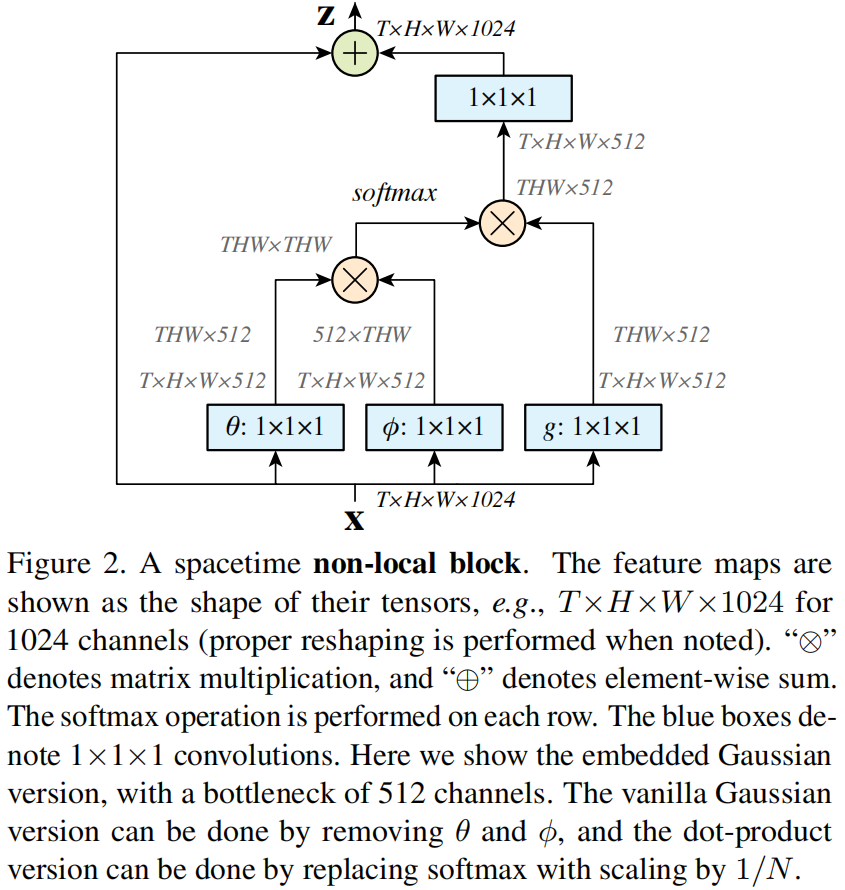
从图中可以看出式 (2), (3), (4) 都可以通过矩阵相乘实现，式 (5) 的拼接就更简单了。

实现细节

block内的中间输出通道数为输入 \(x\) 的一半，即 \(W_{g},W_{\theta},W_{\phi}\)?的输出通道数减半。最后 \(W_{z}\)?再还原回输入通道数。为了进一步减少参数量，在 \(\phi\) 和 \(g\) 的输出后进行 \(2\times 2\) max pooling。

代码

import torch
from torch import nn
from torch.nn import functional as F


# copied from
# https://github.com/AlexHex7/Non-local_pytorch/blob/master/lib/non_local_embedded_gaussian.py
# See https://arxiv.org/abs/1711.07971 for details
class _NonLocalBlockND(nn.Module):
    def __init__(
        self, in_channels, inter_channels=None, dimension=3, sub_sample=True, bn_layer=True
    ):
        super(_NonLocalBlockND, self).__init__()

        assert dimension in [1, 2, 3]

        self.dimension = dimension
        self.sub_sample = sub_sample

        self.in_channels = in_channels
        self.inter_channels = inter_channels

        if self.inter_channels is None:
            self.inter_channels = in_channels // 2
            if self.inter_channels == 0:
                self.inter_channels = 1

        if dimension == 3:
            conv_nd = nn.Conv3d
            max_pool_layer = nn.MaxPool3d(kernel_size=(1, 2, 2))
            bn = nn.GroupNorm  # (32, hidden_dim) #nn.BatchNorm3d
        elif dimension == 2:
            conv_nd = nn.Conv2d
            max_pool_layer = nn.MaxPool2d(kernel_size=(2, 2))
            bn = nn.GroupNorm  # (32, hidden_dim)nn.BatchNorm2d
        else:
            conv_nd = nn.Conv1d
            max_pool_layer = nn.MaxPool1d(kernel_size=2)
            bn = nn.GroupNorm  # (32, hidden_dim)nn.BatchNorm1d

        self.g = conv_nd(
            in_channels=self.in_channels,
            out_channels=self.inter_channels,
            kernel_size=1,
            stride=1,
            padding=0,
        )

        if bn_layer:
            self.W = nn.Sequential(
                conv_nd(
                    in_channels=self.inter_channels,
                    out_channels=self.in_channels,
                    kernel_size=1,
                    stride=1,
                    padding=0,
                ),
                bn(32, self.in_channels),
            )
            nn.init.constant_(self.W[1].weight, 0)
            nn.init.constant_(self.W[1].bias, 0)
        else:
            self.W = conv_nd(
                in_channels=self.inter_channels,
                out_channels=self.in_channels,
                kernel_size=1,
                stride=1,
                padding=0,
            )
            nn.init.constant_(self.W.weight, 0)
            nn.init.constant_(self.W.bias, 0)

        self.theta = conv_nd(
            in_channels=self.in_channels,
            out_channels=self.inter_channels,
            kernel_size=1,
            stride=1,
            padding=0,
        )
        self.phi = conv_nd(
            in_channels=self.in_channels,
            out_channels=self.inter_channels,
            kernel_size=1,
            stride=1,
            padding=0,
        )

        if sub_sample:
            self.g = nn.Sequential(self.g, max_pool_layer)
            self.phi = nn.Sequential(self.phi, max_pool_layer)

    def forward(self, x):
        """
        :param x: (b, c, t, h, w)
        :return:
        """

        batch_size = x.size(0)

        g_x = self.g(x).view(batch_size, self.inter_channels, -1)  # (b,c/2,hw/2)
        g_x = g_x.permute(0, 2, 1)  # (b,hw/2,c/2)

        theta_x = self.theta(x).view(batch_size, self.inter_channels, -1)  # (b,c/2,hw)
        theta_x = theta_x.permute(0, 2, 1)  # (b,hw,c/2)
        phi_x = self.phi(x).view(batch_size, self.inter_channels, -1)  # (b,c/2,hw/2)
        f = torch.matmul(theta_x, phi_x)  # (b,hw,hw/2)
        f_div_C = F.softmax(f, dim=-1)  # (b,hw,hw/2)

        y = torch.matmul(f_div_C, g_x)  # (b,hw,c/2)
        y = y.permute(0, 2, 1).contiguous()  # (b,c/2,hw)
        y = y.view(batch_size, self.inter_channels, *x.size()[2:])  # (b,c/2,h,w)
        W_y = self.W(y)  # (b,c,h,w)
        z = W_y + x

        return z


class NONLocalBlock2D(_NonLocalBlockND):
    def __init__(self, in_channels, inter_channels=None, sub_sample=True, bn_layer=True):
        super(NONLocalBlock2D, self).__init__(
            in_channels,
            inter_channels=inter_channels,
            dimension=2,
            sub_sample=sub_sample,
            bn_layer=bn_layer,
        )