开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 机器人学（一）：构型空间（C-Space） -> 正文阅读

[人工智能]机器人学（一）：构型空间（C-Space）

????????通常情况下，我们对一个机器人提出的最根本问题是，它在哪？这个问题问的是机器人上每一个点的位置在哪。答案就是机器人构型（configuration）：机器人上所有点的位置的表示方法。因为机器人使用的是刚性且形状已知的连杆，所以只需要少量数字就能表示机器人构型。例如，旋转的门的构型，用一个角度就能表示；平面上一点的构型，用两个坐标(x,y)就能表示；平放在桌面的硬币，用(x,y)表示硬币中心的位置，用θ表示硬币上一点的方向，三个变量就能表示其构型。

????????定义：机器人的构型是机器人上每个点的位置的完整表示。表示机器人构型所需的最小实值坐标数n就是机器人的自由度（dof）。包含机器人所有构型的n维空间就是构型空间（C-space）。机器人的构型由其C-space中的一个点表示。

一、自由度（dof）

????????根据上述定义，自由度就是表示机器人构型所需的最小实值坐标数。也就是说，通过这几个实值坐标数就能完整表示机器人上每一点的位置。要了解C-space首先需要确定机器人的自由度。

1.1?刚体自由度

????????平面刚体，表示在二维平面运动的刚体，有3个自由度。空间刚体，表示在三维空间运动的刚体，显然有6个自由度。

????????首先考察一下平面刚体为什么有3个自由度。以放置在桌面的硬币为例如图1所示，按照自由度的定义，需要找到几个参数能完整表示硬币上所有点的位置。所以首先任意选取硬币上的一个点A，用两个参数 $(x_{A},y_{A})$ 就能完全表示A的位置，所以A点有两个自由度。然后再选一个点B，AB之间的距离为 $d_{AB}$ ， $d_{AB}$ 是已知的，因为考察刚体自由度的前提是刚体形状和尺寸是已知的。所以B位于以A为圆心， $d_{AB}$ 为半径的圆上，要确定B的位置，还需要一个参数 $\phi _{AB}$ 。所以要确定A、B的位置需要3个参数 $(x_{A},y_{A},\phi _{AB})$ 。再选一个点C，已知 $d_{AC},d_{BC}$ ，那么C的位置只有两种可能：以A为圆心 $d_{AC}$ 为半径的圆与以B为圆心 $d_{BC}$ 为半径的圆相交处，有两个相交的位置，一首一尾。也就是说，一旦确定了A、B的位置，选定了首尾，确定了常数 $d_{AC},d_{BC}$ ，那么C点的位置就确定了。所以通过 $(x_{A},y_{A},\phi _{AB})$ 就可以确定C的位置。可以尝试再选一个点D，这个点带来了三个额外约束 $d_{AD},d_{BD},d_{CD}$ ，其中有一个是冗余约束。利用另外两个独立约束，就可以类似确定C的位置一样确定D的位置。刚体上其他的点的位置都可以通过这种方法确定，所以放置在桌面的硬币通过三个参数 $(x_{A},y_{A},\phi _{AB})$ 就可以完全确定硬币上所有点的位置。所以平面刚体自由度为3。

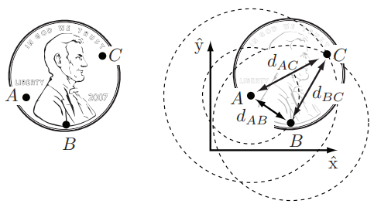
?图1 平面上的硬币

????????这种方法可以总结成：dof=变量个数-约束个数。

????????由以上推导过程可以看出，如果一直三个点的位置，那么可以刚体上其他点的位置也能知道，所以变量个数按照三个点的变量来算。平面刚体上A、B、C的坐标可以表示为 $(x_{A},y_{A}),(x_{B},y_{B}),(x_{C},y_{C})$ ，有6个变量，约束为 $d_{AB},d_{AC},d_{BC}$ ，所以自由度为6-3=3。

????????这种方法也可以用于空间刚体自由度的计算。空间刚体上A、B、C的坐标可以表示为 $(x_{A},y_{A},z_{A}),(x_{B},y_{B}.z_{B}),(x_{C},y_{C},z_{C})$ 有9个变量，约束同样为 $d_{AB},d_{AC},d_{BC}$ ，那么自由度为9-3=6。?

????????所以在空间运动的刚体自由度为6，在平面上运动的刚体自由度为3。

1.2 机器人自由度

?1.2.1 机器人关节

????????典型的机器人关节有六种如图2(a)所示。R表示旋转关节，P表示移动关节，H表示螺旋关节，C表示圆柱关节，U表示万向关节，S表示球形关节。图2(b)总结了各种关节类型提供的自由度和约束。f表示关节自由度个数，c表示关节带来的约束个数。

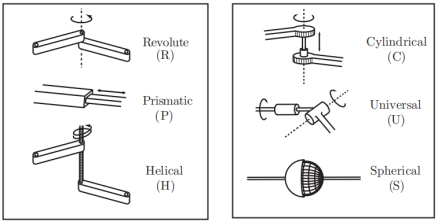
(a)

(b)

图2 典型的机器人关节

?1.2.2 格鲁布勒公式

????????可以通过格鲁布勒公式计算带有关节和连杆机构的自由度。

????????定义：如果机器人有N个连杆，基座也算一个连杆，J表示关节个数，m表示刚体自由度数（如果是平面机构m=3，空间机构则m=6）， $f_i$ 表示第i个关节的自由度， $c_i$ 表示第i个关节的约束个数，对所有关节i， $f_i+c_i=m$ 。机器人的自由度可以按如下格鲁布勒公式计算：

????????其中， $m(N-1)$ 表示除去基座之外所有刚体（连杆）的自由度， $\sum_{i=1}^{J}c_i$ 表示所有关节带来的约束个数。串联机构、并联结构都可以用这种方法计算自由度。

????????这种方法只能用于所有关节约束都是独立的情况。如果它们不是独立的，那么公式提供了自由度的下限。如图3所示的平行四边形连杆机构就是这种情况。连杆个数（包括基座）N=5，关节个数J=6，对于各关节 $f_i=1$ ，对于平面机器人m=3，按上述公式计算自由度为：3(5-1-6)+6=0，自由度为零表示这是一个纯刚性结构，但实际上该机构可以按一个自由度运动。三个平行连杆中的任何一个及其两个关节对机构的运动没有影响，所以关节约束不是独立的，先去掉一个平行连杆及其两个关节，再计算自由度为：dof=3(4-1-4)+4=1。

图3 平行四边形连杆机构?

????????通过这个公式来计算常用的典型平面串联机构，k关节连杆平面串联机器人如图4所示，N=k+1，k个连杆加基座，J=k， $f_i=1$ ，自由度为dof=3((k+1)-1-k)+k=k，对于空间多连杆串联机器人也可以同样计算自由度：dof=6((k+1)-1-k)+k=k，所以通常所说的k关节机器人也可以叫做k自由度机器人。

?图4 平面串联机器人

二、构型空间

2.1 构型空间拓扑

????????上一节主要讲的是怎么确定构型空间的维数（也就是机器人的自由度），然而构型空间的形状也很重要。例如，同样是二维构型空间，一个点在平面上运动与在球面上运动，它们的构型空间显然是不一样的，平面可以无限延伸但球体是环绕的，它们的不同在于构型空间的形状。

????????构型空间形状的不同通过构型空间拓扑来表示。不严格的讲，如果一个空间可以连续变形为另一个空间，而不需要切割或粘合，那么这两个空间在拓扑上是等价的。例如一个大的球面和小的球面是拓扑等价的，但是它们与平面是不等价的，因为不通过剪切是无法将球面变成平面的。

????????一维圆环空间在数学上表示为 $S$ 或 $S^1$ ，直线表示为 $E$ 或 $E^1$ ，表示一维欧几里得空间，由于 $E^1$ 中的点通常用一个实数表示，所以通常写成 $R$ 或 $R^1$ 。一个封闭的线段通常写成 $[a,b]\in R^1$ ，表示包括端点a和b，封闭的线段与直线拓扑不等价，因为直线不包括端点。而一个开放的线段(a,b)与直线是拓扑等价的，因为开放线段可以缩放成直线。

????????对于更高维度而言， $R^n$ 表示n维欧几里得空间， $S^n$ 表示(n+1)维空间里的n维球面，例如 $S^2$ 表示的是在三维空间的二维球面。

????????需要注意的是，空间拓扑结构是空间的一个基本属性，与如何选择坐标来表示空间中的点无关。

????????一些C-空间可以表示为两个或多个低维空间的笛卡尔积，也就是说，这种C空间中的点可以表示为低维空间中点的并集。例如：

1.平面上的刚体的C-space可以表示成 $R^2\times S^1$ ，因为其构型可以用 $(x,y)\in R^2$ 和 $\theta \in S^1$ 表示。

2.一个PR机器人的C-space可以写成 $R^1\times S^1$ 。通常情况下表示C-space拓扑时会忽略关节角度的限制，如果考虑到关节角度限制，C-空间是两个闭合区间的笛卡尔积。

3.一个2R机器人的C-space可以写成 $S^1\times S^1=T^2$ ，其中 $T^n$ 是(n+1)维空间中的n维环面如图5所示。这里需要注意 $S^1\times S^1\times \cdots \times S^1=T^n$ 而不是 $S^n$ 。例如球面 $S^2$ 与二维环面 $T^2$ 不是等价的。

4.一个带有2R机械臂的平面刚体（比如移动机器人），其C-space可以写成 $R^2\times S^1\times T^2=R^2\times T^3$ 。

5.在上一节中讨论的三维空间刚体自由度时，其构型可以用三维点坐标 $R^3$ 、二维球面 $S^2$ 和一维圆环 $S^1$ 表示，所以其C-space可以写成： $R^3\times S^2\times S^1$ 。

?图5 四种不同二维C-space拓扑

2.2 构型空间表示方法

????????为了方便计算，需要用某种代数方式对构型空间进行表示。需要注意的是构型空间的表示方式可以多种多样，但是拓扑是不变的，拓扑是构型空间的根本性质。例如，3D空间中的同一点可以具有不同的坐标表示，具体取决于参考坐标系的选择（坐标轴的原点和方向）和长度比例的选择，但无论如何选择，基本的空间拓扑结构都是相同的。

????????用n个坐标或参数来表示n维构型空间称为空间的显式参数化。例如，二维球面可以用经度和纬度两个参数进行表示，这就是显示表示法。也可以在三维坐标系里面用(x,y,z)表示，这叫隐式表示法。

????????用经纬度表示球面时，当你处于纬度90°或-90°时（南/北极），移动很小一步，就会导致经纬度坐标系的巨大变化。南/北极就是经纬度表示的球面的奇点。这些奇点的位置与球面本身无关，球面在任何地方看起来都是一样的，而一切都与它所选择的表示方法有关。尽管球面上的一点以匀速运动，但在奇点处经纬度坐标系里面的速度趋于无穷。显然这种表示方法会给实际应用带来困难。有两种方法克服这种困难：

用多个显示参数化的坐标系来表示空间，每个坐标系只覆盖空间的一部分，在这一部分内没有奇点。例如，在球面定义两个经纬坐标系，其中一个纬度 $\phi \in [-90^{\circ },90^{\circ }]$ ，经度 $\varphi \in [-180^{\circ },180^{\circ }]$ ，另一个坐标系相当于旋转了90°，在其中一个坐标系的奇点附近就用另一个坐标系来表示，从而避开奇点。

????????用多个坐标系来表示的优点在于，每个坐标都可以用最少的变量个数来表示。一个缺点是需要额外的空间来记录并在各坐标之间切换表示，以避免奇点。需要注意，欧几里德空间可以由一个没有奇点的单坐标系表示。

隐式表示是将n维空间嵌入n维以上的欧几里德空间，就像二维单位球面可以视为嵌入三维欧几里德空间的曲面一样。隐式表示使用的是高维空间的坐标，但这些坐标会受到约束，从而减少自由度的数量。例如单位球面在三维欧几里德空间用(x,y,z)表示，约束为 $x^2+y^2+z^2=1$ 。

????????这种方法的缺点是需要使用多于空间自由度的变量个数。优点是没有奇点，只需要一个坐标系就能表示整个空间。另一个优点是，为闭链机构构建显式参数化表示可能非常困难，但很容易找到隐式表示。隐式表示的一个例子是表示刚体姿态，刚体姿态只需要roll-pitch-yaw三个参数就能表示，但是这种表示存在奇点。而使用九个参数表示，即用旋转矩阵表示，其中有六个约束，这种表示方法除了无奇点之外，旋转矩阵表示法还可以使用线性代数来执行计算，例如旋转刚体或改变表示刚体姿态的参考坐标系。