决策树分类
一、决策树分类简介:
????????决策树方法是利用信息论中的信息增益寻找数据库中具有最大信息量的属性字段,建立决策树的一个结点,再根据该属性字段的不同取值建立树的分支,再在每个分支子集中重复建立树的下层结点和分支的一个过程,构造决策树的具体过程为:首先寻找初始分裂,整个训练集作为产生决策树的集合,训练集每个记录必须是已经分好类的,以决定哪个属性域作为目前最好的分类指标,一般的做法是穷尽所有的属性域,对每个属性域分裂的好坏做出量化,计算出最好的一个分裂,量化的标准是计算每个分裂的多样性指标,其次,重复第一步,直至每个叶节点内的记录都属于同一类且增长到一棵完整的树。
二、选择分叉特征的方式:
(1)基于信息熵的信息增益(ID3)
【定义信息熵】:? ? ? ? ? ? ? ? ? ??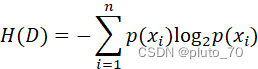 ? ? ? ? ? ???----表示数据混乱程度
? ? ? ? ? ???----表示数据混乱程度
?
当数据类别只有一个时,即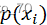 =1,
=1,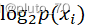 ?=0,故H=0,表示数据纯净,类别越多,H越大。
?=0,故H=0,表示数据纯净,类别越多,H越大。
【定义信息增益】:? ? ? ? ? ? ? ? ? ? ??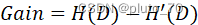 ? ? ----信息增益
? ? ----信息增益
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?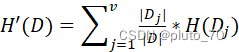
----子节点信息熵
父节点和子节点的信息熵之差,父节点的信息熵叫做“类别信息熵”。子节点的信息熵叫做“条件信息熵”或“属性信息熵”。故信息增益=类别信息熵-属性信息熵。
【举例】:
| 序号 | 天气 | 温度 | 湿度 | 风速 | 高尔夫 |
| 1 | 晴 | 炎热 | 高 | 弱 | 取消 |
| 2 | 晴 | 炎热 | 高 | 强 | 取消 |
| 3 | 阴 | 炎热 | 高 | 弱 | 进行 |
| 4 | 雨 | 适中 | 高 | 弱 | 进行 |
| 5 | 雨 | 寒冷 | 正常 | 弱 | 进行 |
| 6 | 雨 | 寒冷 | 正常 | 强 | 取消 |
| 7 | 阴 | 寒冷 | 正常 | 强 | 进行 |
| 8 | 晴 | 适中 | 高 | 弱 | 取消 |
| 9 | 晴 | 寒冷 | 正常 | 弱 | 进行 |
| 10 | 雨 | 适中 | 正常 | 弱 | 进行 |
| 11 | 晴 | 适中 | 正常 | 强 | 进行 |
| 12 | 阴 | 适中 | 高 | 强 | 进行 |
| 13 | 阴 | 炎热 | 正常 | 弱 | 进行 |
| 14 | 雨 | 适中 | 高 | 强 | 取消 |
?
①计算父节点“类别信息熵”:标签中5个“取消”,9个“进行”
故:? ? ? ? ? ? ? ? ? ? ? ? ? ? ?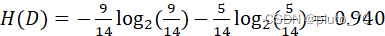
②计算子节点各个“属性信息熵”:即各个属性条件下的类别信息熵,5个晴天条件下存在2个进行,3个取消标签。4个阴天条件下存在4个进行标签。5个雨天条件下存在3个进行,2个取消标签。
【天气】:
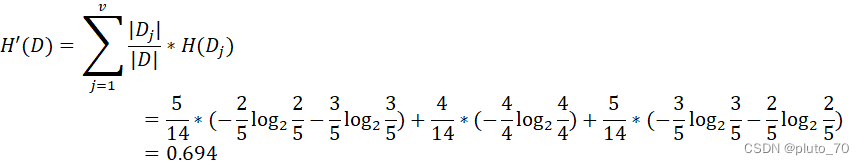
【温度】: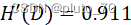 ?
?
【湿度】: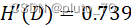 ?
?
【风速】: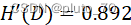 ?
?
③计算各个特征的信息增益
【天气】:
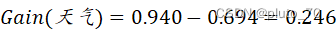 ?
?
【温度】:
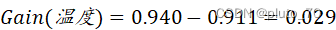 ?
?
【湿度】:
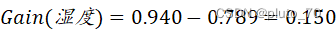 ?
?
【风速】:
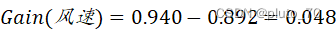 ?
?
选择信息增益最大的【天气】特征作为划分节点
划分后继续进行①==>②==>③步骤,形成分类决策树。????????????????
【信息增益的局限性】:可以清晰的看出,当每个属性中,每种类别都只有一个时,比如【天气】属性下,5个晴天只存在1个进行标签,4个阴天只存在取消标签,5个雨天只存在1个取消标签,那么属性信息熵=0,根据信息增益无法作出有效分叉特征。故使用“信息增益率”对“信息增益”进行改进。
(2)信息增益率(C4.5)
在计算信息增益的基础上定义“属性分裂信息度量”(IV)
【天气】属性中,晴天,雨天,阴天的信息熵,反映了属性本身的混乱程度,若天气属性本身的熵较大,就不倾向于选择它,作为一项分母“惩罚项”来矫正“信息增益”。
?
【天气】:
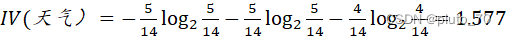 ?
?
【天气信息增益率】:
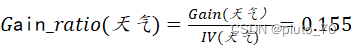 ?
?
同理得其余属性信息增益率:
【温度信息增益率】:
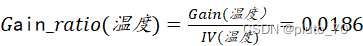 ?
?
【湿度信息增益率】:
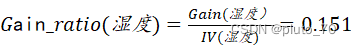 ?
?
【风速信息增益率】:
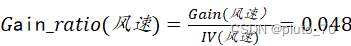 ?
?
发现【天气】属性信息增益率最大,选择天气属性作为分裂特征节点。
(3)基尼系数(CART)
基尼系数遵循最小得原则,计算得到得基尼系数越小,则越纯,接下来就以该特征作为决策树得一个分支。
? ? ? ? ? ? ? ?? ? ?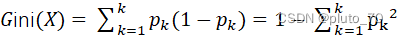 ? ? ? ? ? ? ? ? ? ? ? ? ?----基尼系数
? ? ? ? ? ? ? ? ? ? ? ? ?----基尼系数
然后分支划分后的基尼系数为各个分支的基尼系数以分支概率为权重进行加和。
【天气】:

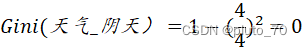
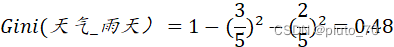
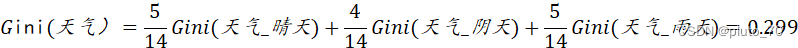
【同理得其余各特征的基尼系数】选择最小得基尼系数所在得特征作为分叉节点。
三、决策树剪枝操作:
?
(1)预剪枝
????????即在生成决策树的过程中提前停止树的增长。核心思想是在树中结点进行扩展之前,先计算当前的划分是否能带来模型泛化能力的提升,如果不能,则不再继续生长子树。此时可能存在不同类别的样本同时存于结点中,按照多数投票的原则判断该结点所属类别。预剪枝对于何时停止决策树的生长有以下几种方法:
①当树到达一定深度的时候,停止树的生长。
②当到达当前结点的样本数量小于某个阈值的时候,停止树的生长。
③计算每次分裂对测试集的准确度提升,当小于某个阈值的时候 ,不再继续扩展。
预剪枝具有思想直接、算法简单、效率高等特点,适合解决大规模问题。但如何准确地估计何时停止树的生长(即上述方法中的深度或阈值),针对不同问题会有很大差别,需要一定经验判断。且预剪枝存在一定局限性,高欠拟合的风险,虽然当前的划分会导致测试集准确率降低,但在之后的划分中,准确率可能会高显著上升。
(2)后剪枝
????????在已经生成的过拟合决策树上进行剪枝,得到简化版的剪枝决策树。核心思想是让算法生成一棵完全生长的决策树,然后从最底层向上计算是否剪枝。剪枝过程将子树删除,用一个叶子结点替代,该结点的类别同样按照多数投票的原则进行判断。同样地,后剪枝也可以通过在测试集上的准确率进行判断,如果剪枝过后准确率有所提升,则进行剪枝。 相比于预剪枝,后剪枝方法通常可以得到泛化能力更强的决策树,但时间开销会更大。
??????常见的后剪枝方法包括错误率降低剪枝(Reduced Error Pruning, REP)、悲观剪枝(Pessimistic Error Pruning, PEP)、代价复杂度剪枝(Cost Complexity Pruning, CCP)、最小误差剪枝(Minimum Error Pruning, MEP)、 CVP (Critical Value Pruning)、 OPP (Optimal Pruning)等方法,这些剪枝方法各有利弊,关注不同的优化角度。
四、决策树实例及代码(python实现):
说明:
?
1、包含“信息增益”和“基尼系数”两种特征选择方式
2、包含“预剪枝”和“后剪枝”两种剪枝操作
3、包含两种数据集,文中的例子和“西瓜书的数据集”,两个excel文件图片展示如下。
天气:
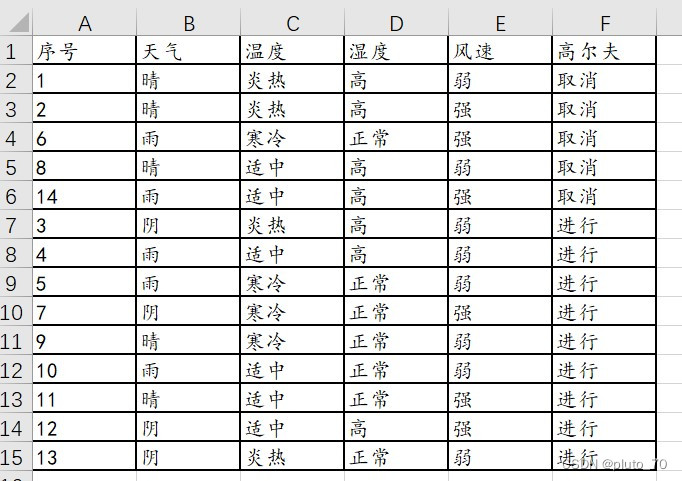
西瓜集:
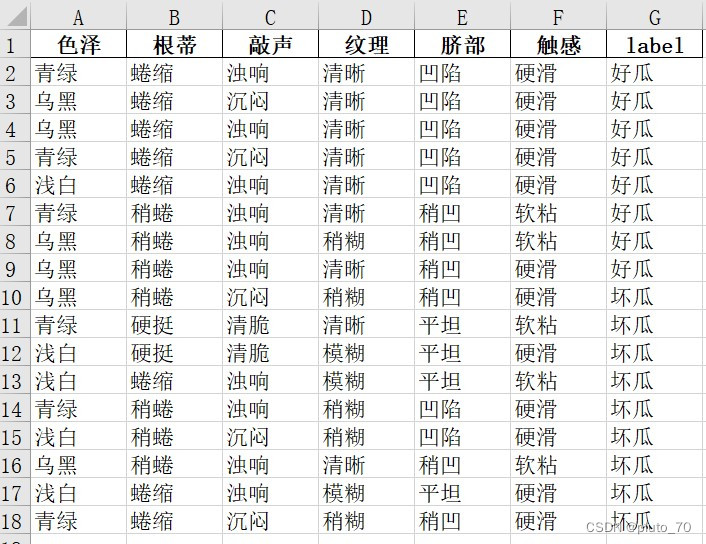
完整代码如下:
import numpy as np
import operator
import pandas as pd
def GetData_weather():
path = "F://天气表.xlsx"
data = pd.read_excel(path, header=None, names=["天气", "温度", "湿度", "风速", "高尔夫"])
clos = data.shape[1] # 获取列数
all_data = data.iloc[:, 0:clos]
all_data = np.delete(np.array(all_data), 0, axis=0) # 删除首行
labels = data.columns.tolist() # ["天气", "温度","湿度","风速","高尔夫"]
labels.pop() # ["天气", "温度","湿度","风速"}
newdata = all_data
trainIndex = [0, 1, 2, 3, 5, 6, 9, 13]
trainDataSet = np.array(newdata[trainIndex]) # 选取了一部分作为训练集
# 得到剪枝数据集
pruneIndex = [4, 7, 8, 10, 11, 12]
pruneDataSet = np.array(newdata[pruneIndex]) # 得到训练数据集
return trainDataSet, pruneDataSet, np.array(labels)
def GetData_watermelon():
path = "F://西瓜集.xlsx"
data = pd.read_excel(path, header=None, names=["色泽", "根蒂","敲声","纹理","脐部","触感","label"])
clos = data.shape[1] # 获取列数
all_data = data.iloc[:, 0:clos]
all_data = np.delete(np.array(all_data), 0, axis=0) # 删除首行
labels = data.columns.tolist()
labels.pop()
newdata = all_data
trainIndex = [0, 1, 2, 5, 6, 9, 13, 14, 15, 16, 3]
trainDataSet = np.array(newdata[trainIndex]) # 选取了一部分作为训练集
# 得到剪枝数据集
pruneIndex = [4, 7, 8, 10, 11, 12]
pruneDataSet = np.array(newdata[pruneIndex]) # 得到训练数据集
return trainDataSet, pruneDataSet, np.array(labels)
def dataset_entropy(dataset): # 两种计算方式的函数名一样,为了方便
"""
计算数据集的基尼系数
"""
classLabel = dataset[:, -1] # 标签
labelCount = {}
for i in range(classLabel.size):
label = classLabel[i]
labelCount[label] = labelCount.get(label, 0) + 1
# 熵值(第一步)
Gini = 1.0
for k, v in labelCount.items():
Gini -= float(v / classLabel.size) * float(v / classLabel.size)
return Gini
# def dataset_entropy(dataset):
# """
# 计算数据集的信息熵
# """
# classLabel = dataset[:, -1] # 标签
# labelCount = {}
# for i in range(classLabel.size):
# label = classLabel[i]
# labelCount[label] = labelCount.get(label, 0) + 1
# # 熵值(第一步)
# cnt = 0
# for k, v in labelCount.items():
# cnt += -v / classLabel.size * np.log2(v / classLabel.size)
# return cnt
# 接下来切分,然后算最优属性
def splitDataSet(dataset, featureIndex):
'''
划分每个特征隶属于每个“属性”的子集,构建所有子集的集合subdataset
subdataset下的每个子集,一是作为下一次分裂的数据集,二是计算本次特征下的“属性信息熵”
'''
subdataset = []
featureValues = dataset[:, featureIndex] # 取出第i列特征
featureSet = list(set(featureValues)) # 去重,统计该特征具有的属性
for i in range(len(featureSet)): # 划分该属性的子集
newset = []
for j in range(dataset.shape[0]): # 依次循环该特征的每一行
if featureSet[i] == featureValues[j]: # 找出同属一属性的索引行
newset.append(dataset[j, :]) # 将同属于一个属性的样本放置新列表
newset = np.delete(newset, featureIndex, axis=1) # 只用到标签列计算熵,删除此特征得到下一层的数据集
subdataset.append(np.array(newset)) # 下一层的数据集就得到了
return subdataset # 得到根据此特征中的“属性”划分出来的子集作为下一层的数据集
def splitDataSetByValue(dataset, featureIndex, value):
subdataset = []
# 迭代所有的样本
for example in dataset:
if example[featureIndex] == value:
subdataset.append(example)
if not subdataset:
return subdataset
return np.delete(subdataset, featureIndex, axis=1)
def chooseBestFeature(dataset, labels):
"""
选择最优特征,但是特征是不包括名称的。
如何选择最优特征:每一个特征计算,信息增益最大==条件熵最小就可以。
"""
# 特征的个数
featureNum = labels.size # 特征的个数
# 设置最小熵值
minEntropy, bestFeatureIndex = 1, None
# 样本总数
n = dataset.shape[0] # 取行数即样本数量
for i in range(featureNum): # 依次计算每个特征
# 指定特征的条件熵
featureEntropy = 0
# 返回所有子集
allSubDataSet = splitDataSet(dataset, i) # 根据第i个特征“属性”划分出来的子集集合 ****************************************************
for subDataSet in allSubDataSet: # 遍历每个子集,计算该“属性信息熵”
featureEntropy += subDataSet.shape[0] / n * dataset_entropy(subDataSet) # 每个特征下(sum(每个属性/总行数 * 各属性的熵))
if minEntropy > featureEntropy: # 迭代比较每个特征下的熵的大小,若更小,则赋值给min
minEntropy = featureEntropy # 赋值
bestFeatureIndex = i # 最佳的分类特征就选出来了
return bestFeatureIndex # 最佳增益的特征i
def mayorClass(classList):
labelCount = {}
for i in range(classList.size): # 标签列的行数
label = classList[i]
labelCount[label] = labelCount.get(label, 0) + 1 # 若字典中不存在则+1 统计标签类别出现的次数
sortedLabel = sorted(labelCount.items(), key=operator.itemgetter(1), reverse=True) # 对各类别出现的次数进行排序,也就是值,从大到小排序
return sortedLabel[0][0] # 返回投票次数最多的类别
def createTree(dataset, labels):
classList = dataset[:, -1] # 标签列
#*************************递归退出机制*******************************************#
if len(set(dataset[:, -1])) == 1:# 当类别完全相同停止划分
return dataset[:, -1][0] # 返回此类别
if labels.size == 0 or len(dataset[0]) == 1: # 当“属性用尽”,停止划分
return mayorClass(classList) # 返回投票最多的类别
#*************************递归退出机制*******************************************#
bestFeatureIndex = chooseBestFeature(dataset, labels) # 选择最佳分类特征第i列
bestFeature = labels[bestFeatureIndex] # 该特征的名称也选出来了
dtree = {bestFeature: {}} # 用代码表示这棵树,二级字典
featureList = dataset[:, bestFeatureIndex] # 最佳的特征列也选出来了
featureValues = set(featureList) # 该特征下的“属性”集合
for value in featureValues:
subdataset = splitDataSetByValue(dataset, bestFeatureIndex, value) # 原数据集、最佳分裂特征列索引、属性
sublabels = np.delete(labels, bestFeatureIndex) # 同时删除最佳特征所在列的名称
dtree[bestFeature][value] = createTree(subdataset, sublabels) # 递归下去,两个条件:1、当类别完全相同则停止继续划分 2、属性用尽停止划分
return dtree
def predict_class(inputTree, featLabels, testVec): #传入参数:决策树,属性标签,待分类样本
firstStr = list(inputTree.keys())[0] #树根代表的属性
secondDict = inputTree[firstStr]
classlabell = None
featIndex = featLabels.index(firstStr) #树根代表的属性,所在属性标签中的位置,即第几个属性
for key in secondDict.keys():
if testVec[featIndex] == int(key):
if type(secondDict[key]).__name__ == 'dict':
classlabell = predict_class(secondDict[key], featLabels, testVec)
else:
classlabell = secondDict[key]
return classlabell # 返回测试集的类别
'''剪枝操作'''
def cntAccNums(dataSet, pruneSet):
"""
用于剪枝,用dataSet中多数的类作为节点类,计算pruneSet中有多少类是被分类正确的,然后返回正确
分类的数目。
:param dataSet: 训练集
:param pruneSet: 测试集
:return: 正确分类的数目
"""
nodeClass = mayorClass(dataSet[:, -1])
rightCnt = 0
for vect in pruneSet:
if vect[-1] == nodeClass:
rightCnt += 1
return rightCnt
def prePruning(dataSet, pruneSet, labels):
classList = dataSet[:, -1]
if len(set(classList)) == 1:
return classList[0]
if len(dataSet[0]) == 1:
return mayorClass(classList)
# 获取最好特征
bestFeat = chooseBestFeature(dataSet, labels) # √
bestFeatLabel = labels[bestFeat] # 获取特征名称
sublabels = np.delete(labels, bestFeat) # 从特征名列表删除
# 计算初始正确率
baseRightNums = cntAccNums(dataSet, pruneSet)
# 得到最好划分属性取值
featureList = dataSet[:, bestFeat] # 最佳的特征列也选出来了
features = set(featureList) # 取出特征下的属性集合
# 计算尝试划分节点时的正确率
splitRightNums = 0.0
for value in features: # 遍历每一个属性
# 每个属性取值得到的子集
subDataSet = splitDataSetByValue(dataSet, bestFeat, value)
if len(subDataSet) != 0:
# 把用来剪枝的子集也按照相应属性值划分下去
subPruneSet = splitDataSetByValue(pruneSet, bestFeat, value)
# if value == "凹陷":
# print(subPruneSet)
splitRightNums += cntAccNums(subDataSet, subPruneSet)
if baseRightNums < splitRightNums: # 如果不划分的正确点数少于尝试划分的点数,则继续划分。
myTree = {bestFeatLabel: {}}
else:
return mayorClass(dataSet[:, -1]) # 否则,返回不划分时投票得到的类
# 以下代码和不预剪枝的代码大致相同,一点不同在于每次测试集也要参与划分。
for value in features:
subDataSet = splitDataSetByValue(dataSet, bestFeat, value)
subPruneSet = splitDataSetByValue(pruneSet, bestFeat, value)
if len(subDataSet) != 0:
myTree[bestFeatLabel][value] = prePruning(subDataSet, subPruneSet, sublabels)
else:
# 计算D中样本最多的类
myTree[bestFeatLabel][value] = mayorClass(classList)
return myTree
def postPruning(dataSet, pruneSet, labels):
classList = dataSet[:, -1]
# 如果基尼指数为0,即D中样本全属于同一类别,返回
if len(set(classList)) == 1:
return classList[0]
# 属性值为空,只剩下类标签
if len(dataSet[0]) == 1:
return mayorClass(classList)
# 得到增益最大划分的属性、值
bestFeat = chooseBestFeature(dataSet, labels)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel: {}} # 创建字典,即树的节点。
# 生成子树的时候要将已遍历的属性删去。数值型不要删除。
sublabels = np.delete(labels, bestFeat)
featureList = dataSet[:, bestFeat] # 最佳的特征列也选出来了
uniqueVals = set(featureList) # 取出特征下的属性集合
for value in uniqueVals: # 标称型的属性值有几种,就要几个子树。
# Python中列表作为参数类型时,是按照引用传递的,要保证同一节点的子节点能有相同的参数。
subPrune = splitDataSetByValue(pruneSet, bestFeat, value)
subDataSet = splitDataSetByValue(dataSet, bestFeat, value)
if len(subDataSet) != 0:
myTree[bestFeatLabel][value] = postPruning(subDataSet, subPrune, sublabels)
else:
# 计算D中样本最多的类
myTree[bestFeatLabel][value] = mayorClass(classList)
# 后剪枝,如果到达叶子节点,尝试剪枝。
# 计算未剪枝时,测试集的正确数
numNoPrune = 0.0
for value in uniqueVals:
subDataSet = splitDataSetByValue(dataSet, bestFeat, value)
if len(subDataSet) != 0:
subPrune = splitDataSetByValue(pruneSet, bestFeat, value)
numNoPrune += cntAccNums(subDataSet, subPrune)
# 计算剪枝后,测试集正确数
numPrune = cntAccNums(dataSet, pruneSet)
# 比较决定是否剪枝, 如果剪枝后该节点上测试集的正确数变多了,则剪枝。
if numNoPrune < numPrune:
return mayorClass(dataSet[:, -1]) # 直接返回节点上训练数据的多数类为节点类。
return myTree
def run():
'''主函数'''
dataset,prunedata,labels = GetData_watermelon()
'''不剪枝'''
mytree = createTree(dataset, labels)
print(mytree)
'''预剪枝'''
preTree = prePruning(dataset, prunedata, labels)
print(preTree)
'''后剪枝'''
postTree = postPruning(dataset, prunedata, labels)
print(postTree)
if '__main__' == __name__:
run()?
?
?
?
?
?
参考资料:
- https://wwwhttps://blog.csdn.net/ylhlly/article/details/93213633?spm=1001.2014.3001.5506.jianshu.com/p/b90a9ce05b28
- https://www.csdn.net/tags/NtTaYg1sMjU5MjItYmxvZwO0O0OO0O0O.html
- 周志华《机器学习》
?
?
