分类思想
逻辑回归(Logistic Regression)虽然称为回归,但实际是一个常用的二分类算法,用来表示某件事发生的可能性。分类的思想:将每个样本进行“打分”,然后设置一个阈值(概率),大于该阈值为一个类别,反之另一类别。
逻辑回归模型公式
逻辑回归的z部分类似线性回归,z值是一个连续的值,取值范围为
z
∈
(
?
∞
,
+
∞
)
z\in(-\infin,+\infin)
z∈(?∞,+∞),将阈值设为0,当z≥0时,样本划为“正类”,当z<0时,样本划为“负类”,这种分类对整改是实数域敏感一致不便于分类。
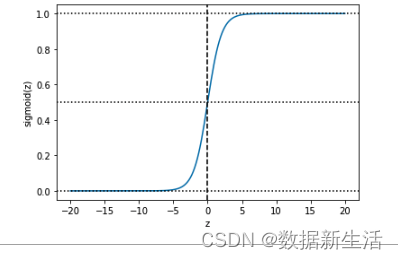
在z的基础上,套上sigmoid函数(引入非线性映射),将线性回归值域映射至(0,1),将预测值限制在(0,1),模型曲线在z=0时,十分敏感,在z>>>0 or z<<<0时都不敏感,有助于直观做出列别判断,>0为“正类”,反之为“负类”。
z
=
θ
1
x
1
+
θ
1
x
2
+
.
.
.
+
θ
n
x
n
+
b
=
∑
i
=
1
n
θ
i
x
i
+
b
=
∑
i
=
0
n
θ
i
x
i
=
θ
T
X
.
h
θ
(
x
)
=
s
i
g
m
o
i
d
(
z
)
=
1
1
+
e
?
θ
T
X
z = \theta_1x_1+\theta_1x_2+...+\theta_nx_n+b =\textstyle\sum_{i=1}^n\theta_ix_i+b=\textstyle\sum_{i=0}^n\theta_ix_i=\theta^TX \\. \\ h_\theta(x)=sigmoid(z)=\frac{1}{1+e^{-\theta^TX}}
z=θ1?x1?+θ1?x2?+...+θn?xn?+b=∑i=1n?θi?xi?+b=∑i=0n?θi?xi?=θTX.hθ?(x)=sigmoid(z)=1+e?θTX1?
- 模型学习训练的本质
通过带有n个特征{ x 1 , x 2 . . . x n x_1,x_2...x_n x1?,x2?...xn?}的观测样本的拟合参数{ θ 1 , θ 2 . . . θ n \theta_1,\theta_2...\theta_n θ1?,θ2?...θn?},拟合出参数就得到了z曲线,也就得到了模型的决策边界来进行分类,参数的拟合就是模型训练学习的本质。
如果z是二元一次函数,则决策边界就是一条直线,将二维平面进行分类划分。训练集不可以定义决策边界,只是负责去拟合参数,尽可能地贴近真实。
公式推导
sigmoid函数
y
=
s
i
g
m
o
i
d
(
z
)
=
1
1
+
e
?
z
,
z
∈
(
?
∞
,
+
∞
)
,
y
∈
(
0
,
1
)
y=sigmoid(z)=\frac{1}{1+e^{-z}}, z\in(-\infin,+\infin), y\in(0,1)
y=sigmoid(z)=1+e?z1?,z∈(?∞,+∞),y∈(0,1)