其他知识的补充:
最典型的MLP包括包括三层:输入层、隐藏层和输出层,MLP神经网络不同层之间是全连接的(全连接的意思就是:上一层的任何一个神经元与下一层的所有神经元都有连接)。
神经网络主要有三个基本要素:权重、偏置和激活函数。
权重告诉神经元需要关注什么样的像素图案。权重有点像连接的强弱。
偏置告诉你加权和得有多大才能让神经元的激发变得有意义。而偏置值表示神经元是否更容易被激活。
激活函数:起非线性映射的作用,其可将神经元的输出幅度限制在一定范围内,一般限制在(-11)或(01)之间。最常用的激活函数是Sigmoid函数,其可将(-∞,+∞)的数映射到(0~1)的范围内。
激活函数还有tanh和ReLU等函数,tanh是Sigmoid函数的变形,tanh的均值是0,在实际应用中有比Sigmoid更好的效果;ReLU是近来比较流行的激活函数,当输入信号小于0时,输出为0;当输入信号大于0时,输出等于输入;具体采用哪种激活函数需视具体情况定。
代价函数:
对于每一个训练样本,将每个输出层的神经元(比如说输出层有9个神经元)输出的值和准确值相减后平方,然后相加。这就是训练单个样本的“代价”。
然后需要对所有的训练样本(比如说有几万个训练样本)的代价求平均值,用这个平均值来评价这个网络的好坏。
代价函数可以理解为:输入的是13002个权重和偏置值;输出的是一个数值,这个数值表示这些参数有多差劲/优秀
那么要怎么改变这些权重或偏置值才能使结果最好(寻找函数的最小值)呢?
先考虑一元函数的情况,只有一个输入变量一个输出变量。可以先随便挑选一个输入值,然后考虑向左走还是向右走,函数值才会变小。也就是说找到这点的斜率,斜率为正,就向左走,斜率为负,就向右走。每一步都这样重复,就可以逼近函数的某个局部最小值。但是注意局部最小值并不一定是全局最小值。还有一点,如果每步的大小和斜率成比例,也就是斜率大步长就大,那么在最小值附近斜率就会越来越平缓,步长会越来越小,这样可以防止调过头。
再来考虑二元函数的情况,两个输入一个输出。
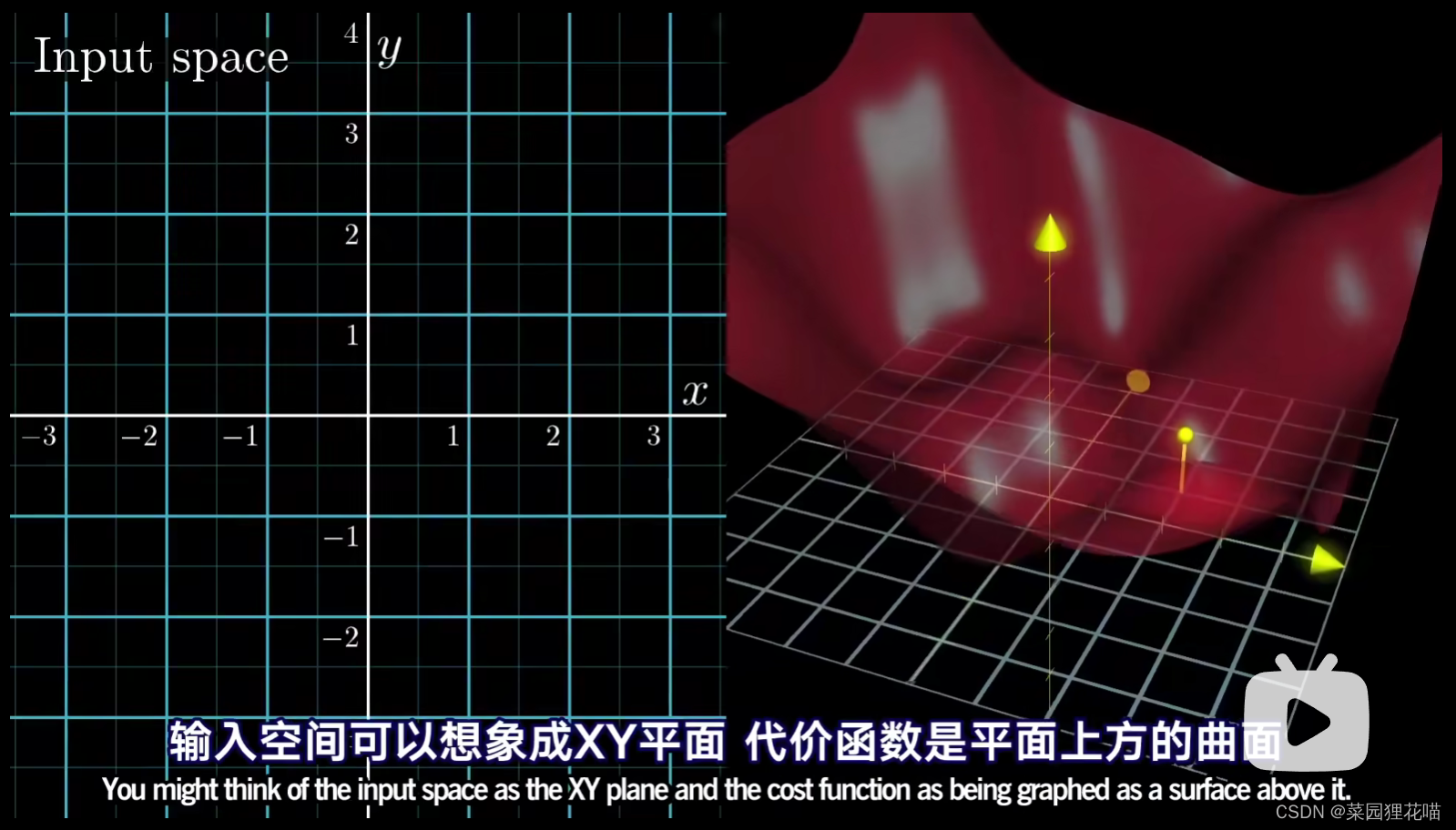
这样就不是考虑函数的斜率,而是考虑在输入空间内沿哪个方向走,才能下降地最快。由微积分知识可以知道,函数的梯度指出了函数的最陡增长方向,那么沿梯度的负方向走,函数值就降低地最快了。梯度向量的长度就代表了这个最陡的斜坡到底有多陡(多元微积分相关的课程可以移步三蓝一棕在可汗学院上做的多元微积分课程)。所以其实让函数值最小的算法就是先计算梯度,再按梯度的反方向走一步,然后循环。
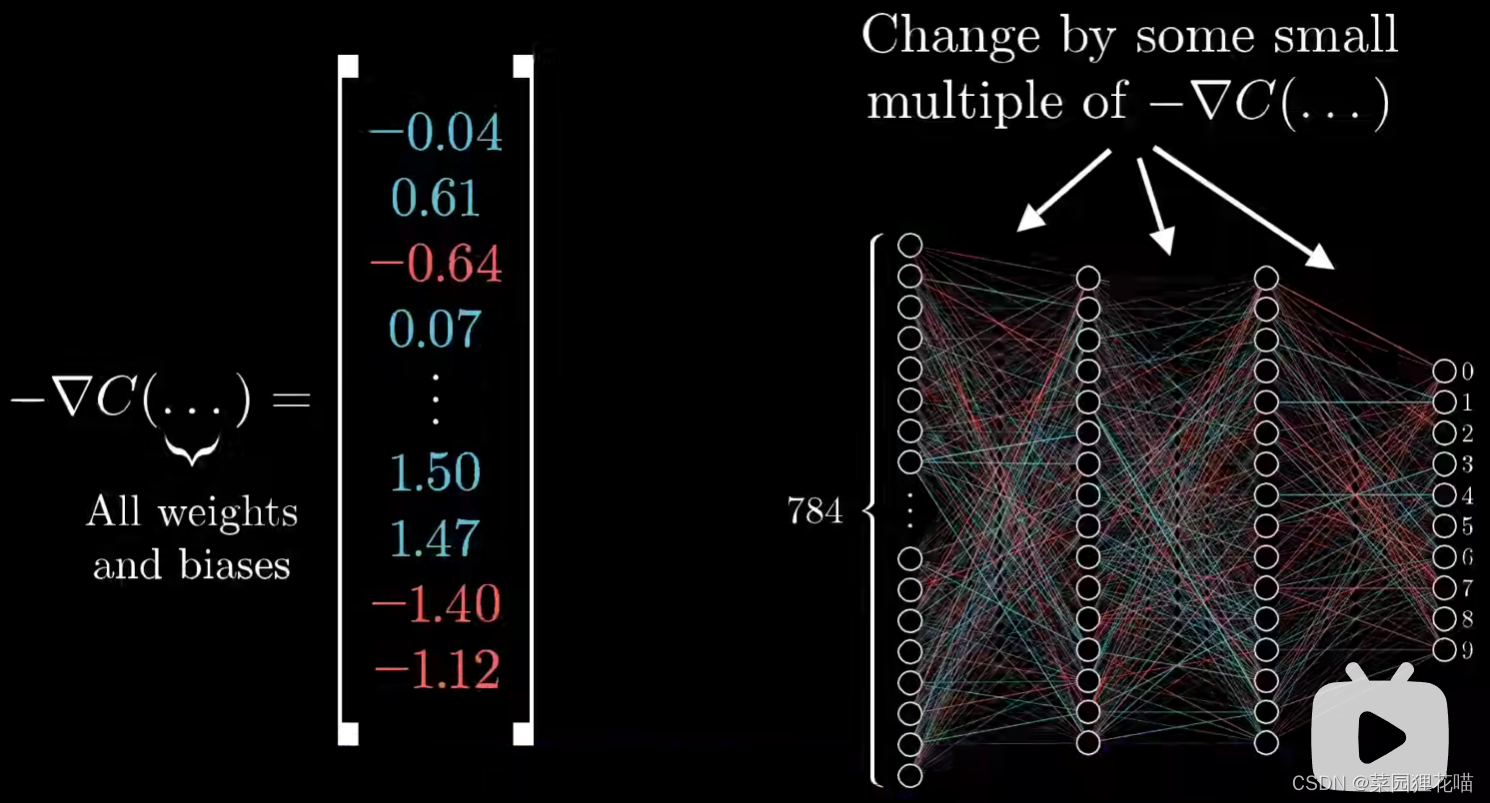
处理有13000个输入的函数也是一样的道理。想象把13000个权重偏置都放到一个列向量里,那么代价函数的负梯度也不过是个向量

负梯度正是指出了在这个大到爆炸的函数输入空间内,具体如何改变哪一项参数,才可以让代价函数的值下降得最快。那么对于这个特别设计的代价函数,更新权重和偏置来降低代价函数的值意味着输入训练集的每一份样本的输出都更接近期待的真实结果。这个代价函数取了整个训练集的平均值,所以最小化的意思是,对所有的样本得到的总体结果都会更好。这个计算梯度的算法是神经网络的核心,也就是反向传播算法(BP,back propagation)。
让网络学习,实质上就是让代价函数的值最小,为了达到这个结果,代价函数非常有必要是平滑的,这样才能每次挪一点点,最后找到一个局部最小值。这也解释了为什么人工神经元的激活值是连续的,而非直接沿袭生物学神经元那种二元式的,要么激活要么非激活的取值模式。这种按照负梯度的倍数,不停调整函数输入值的过程,就叫做梯度下降法。这是一种可以收敛到代价函数图中某一个“坑”里,即一个局部最小值的地方。其实负梯度中的每一项都告诉了两件事,正负号告诉我们输入向量的这一项该调大还是调小,但更重要的是每一项的相对大小告诉了我们改变哪个值的影响更大。对于训练数据来说,就是其中某些连线就更加地重要。所以代价函数的梯度向量就可以理解为各个权重偏置的相对重要度,它标记出了改变哪个参数的性价比最高。这也是理解方向的另一种方式,举个例子,假设有个输入两个变量的二元函数,计算出来这个函数在某点的梯度是[3,1],一种解读就是你站在这个点,顺着这个梯度的方向移动,函数值增加得最快,当把这个函数曲面画出来时,沿这个向量的方向走就是径直向上的。
还有另外一种解读,即第一个变量的重要性是第二个变量的3倍。也就是说在这一块的取值区域内,改变x值会造成更大的影响。
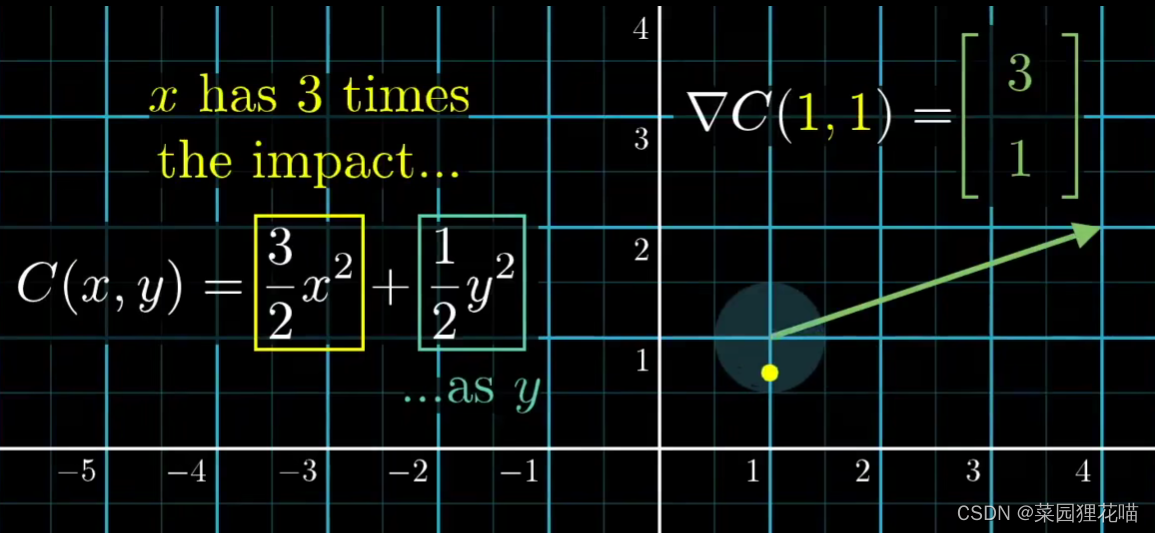
小结:
神经网络本身是一个带784个输入和10个输出的函数,由各种加权和所定义
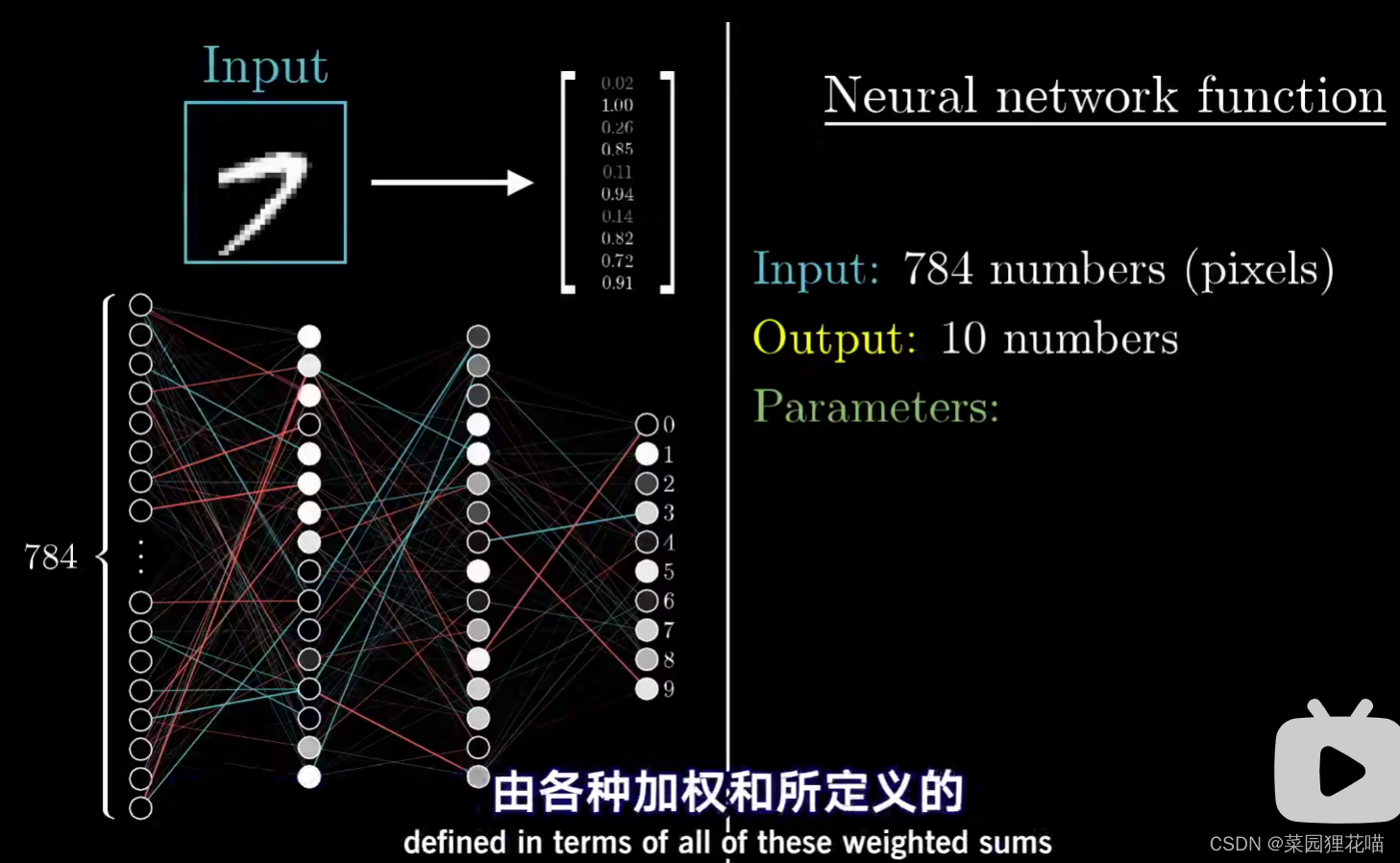
代价函数则是更复杂一层,把13000多个权重偏置作为输入,通过训练数据,得出一个对网络糟糕程度的评分。
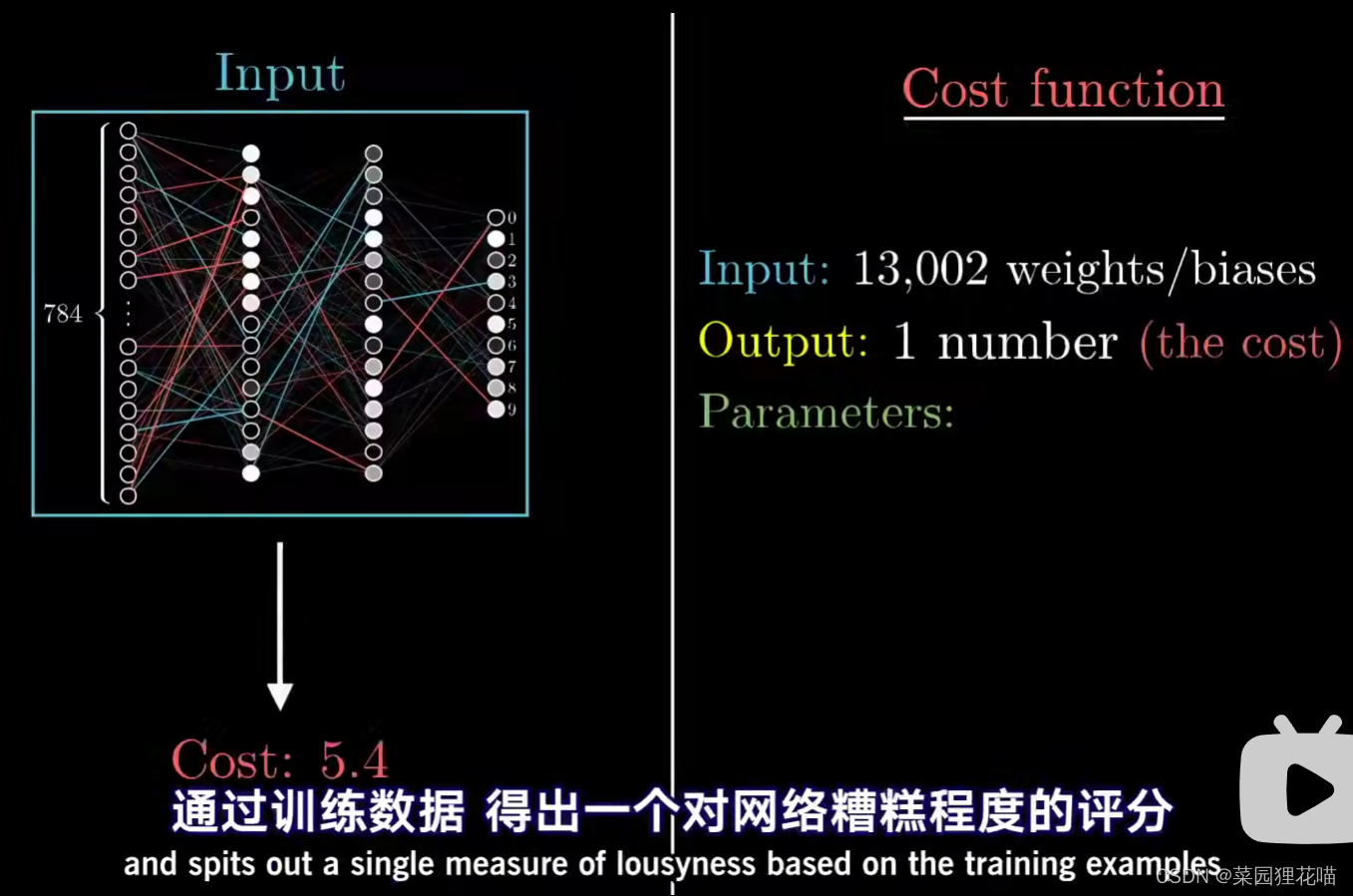
而代价函数的梯度,则在上边还要复杂一层,告诉我们如何微调权重偏置的值才可以让代价函数的结果改变得最快,也就是改变了哪些权重的影响力最大。
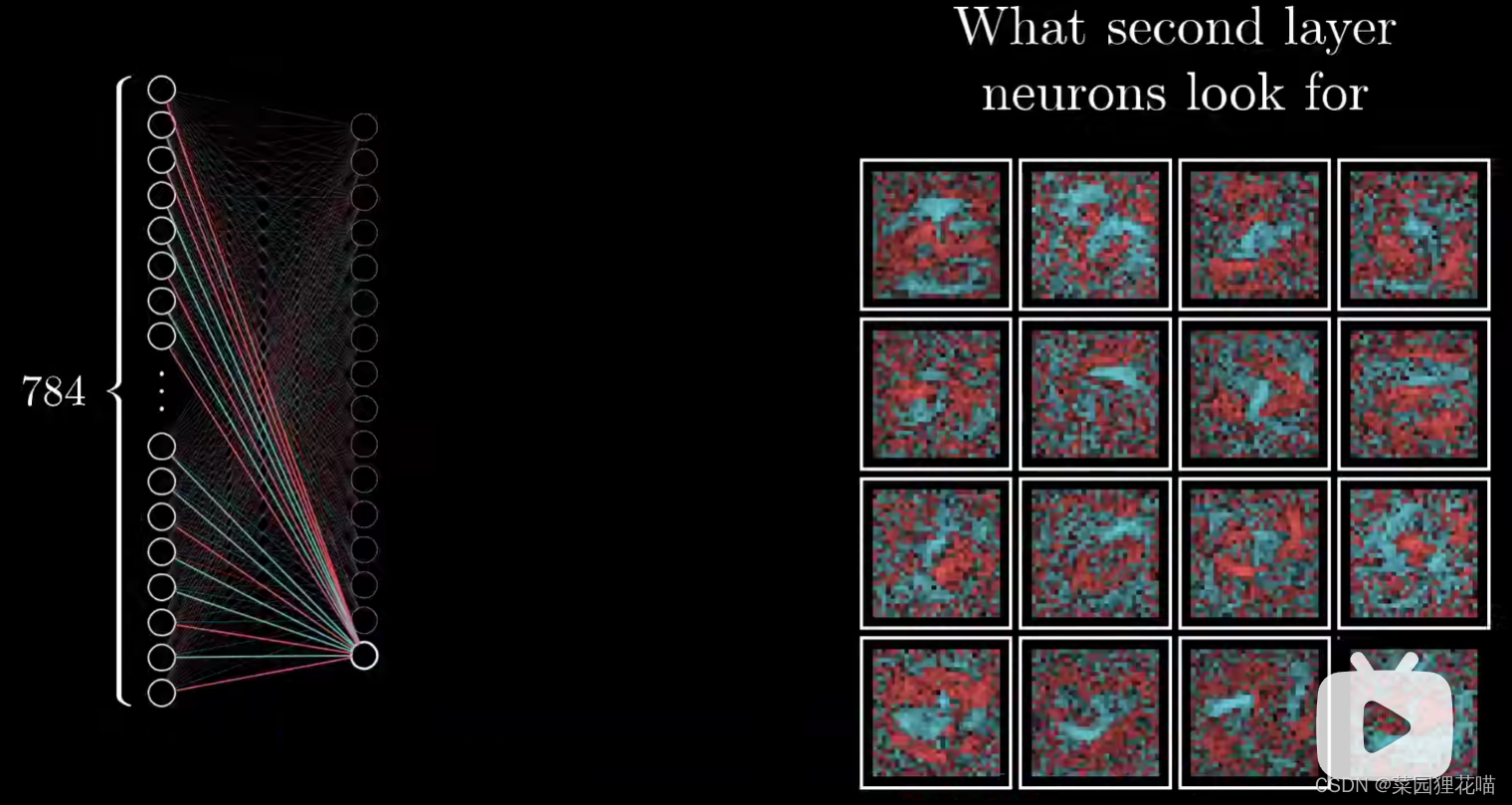
一开始up主介绍这种结构期望的是第2层可以识别出短边,第三层可以把短边拼成圈或者长笔画,最后把这些部件拼成数字。但是神经网络真的是这样做的吗?并不是。
之前我们可以把第一层所有神经元和第二层某一神经元间所有的权重表示为第二层神经元所识别的一个像素图案。然而实际运用中,第一层和第二层之间的权重与其说它们能识别出各种散落的短边,但其实它们看起来并没有什么规律,中间只有一些松散的图案,感觉就像在如深海一般的13000维的参数空间中网络找到了一个还不错的局部最小值住了下来,尽管它可以成功对绝大多数图像做分类,但它并不会如期望一般识别出图像中的各种图案
一个例子就是如果把一个随机的图像输入进去(并非手写数字的图像),那么我们会期待它会感到不确定,10个输出神经元一个都不激活,或者10个全部激活且激活值都差不多,但结果确是网络总能很自信地给出一个没道理的回答。网络可以把一个数字5识别为5,也会把一个随机的噪声图像识别为5。也就是说虽然网络可以很好地识别数字,但是它也并不知道自己如何写数字,究其原因,很大程度上是因为它的训练被限定在了很窄的框架内。从神经网络的角度来看,整个宇宙都是由小网格内清晰定义的静止数字所组成,而代价函数只会促使它对最后的判断有绝对的自信
推荐的学习资料:
推荐Michael Nielsen介绍神经网络和深度学习的书:https://goo.gl/Zmczdy
,它着重讲解了许多可供下载的代码和数据,其中就包括我在这个视频里举的例子。主动学***!
https://github.com/mnielsen/neural-networks-and-deep-learning
我同样很推荐Chris Olah的博客:http://colah.github.io/

想看更多视频的话,Welch Labs也有许多不错的机器学习视频系列:
https://youtu.be/i8D90DkCLhI
https://youtu.be/bxe2T-V8XRs
想学得再深一些的话,可以看看Goodfellow, Bengio, Courville合著的课本"Deep Learning"。
此外,Distill的文章写得也很精彩:https://distill.pub/
所谓的学习,就是指要找到特定的权重偏置,从而使代价函数最小化。
梯度向量每一项的大小就是告诉你代价函数对每个参数有多敏感
先以识别数字2为例,若想让最后一层输出层的对应的输出为2的神经元信号变强,可以通过改变上一层的权重+改变上一层各个神经元的激活值(也就是改变上上一层的权重)来实现,同样也需要用相同的方法来使非输出为2的其余神经元相应的权重改变。所以关于如何改变倒数第二层,我们会把数字2神经元的期待和别的输出神经元的期待全部加起来,作为如何改变倒数第二层神经元的指示。这些期待变化不仅仅是对应的权重的倍数,也是每个神经元激活值该变量的倍数,这其实就是在实现“反向传播”的理念了。
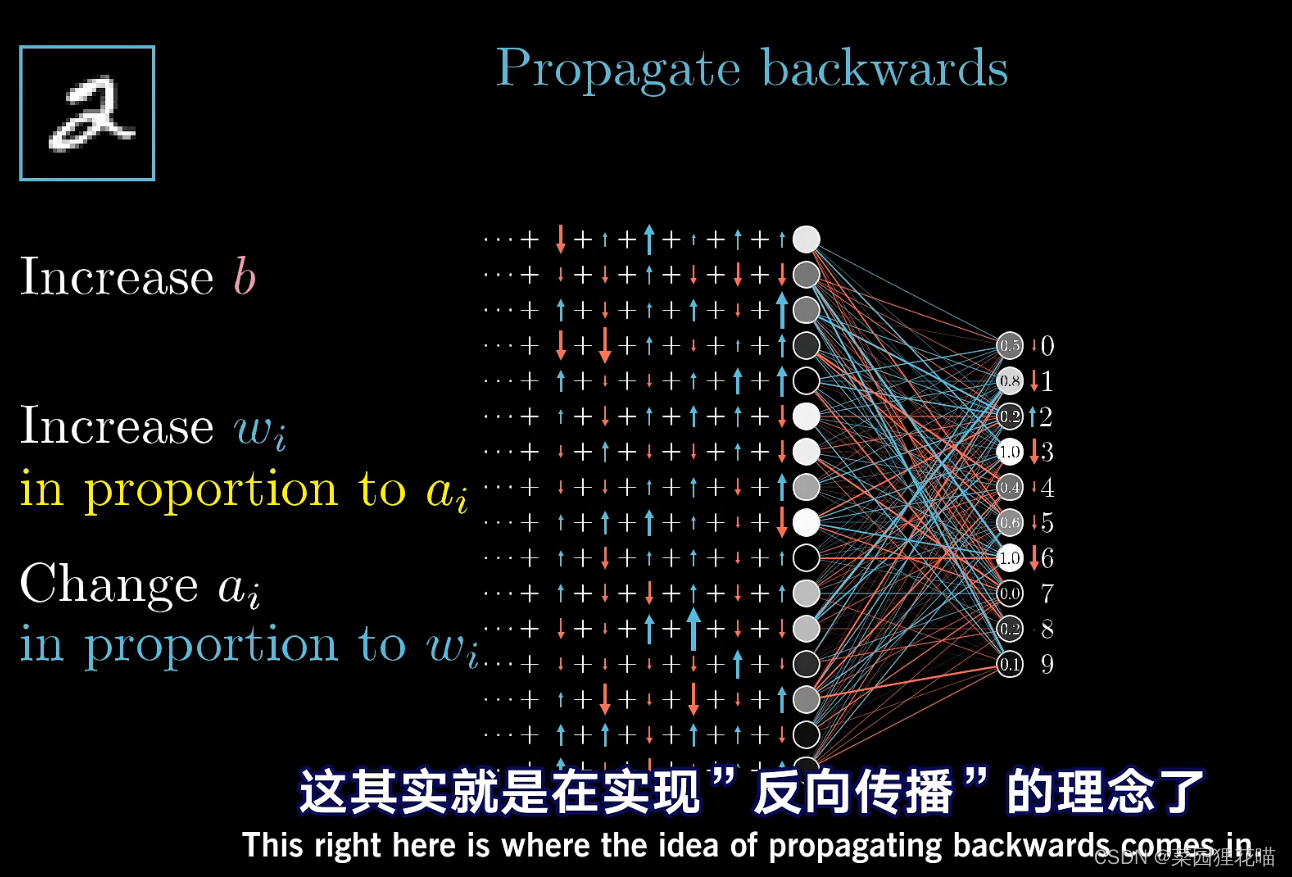
把所有期待的改变加起来,就得到了一串对倒数第二层改动的变化量
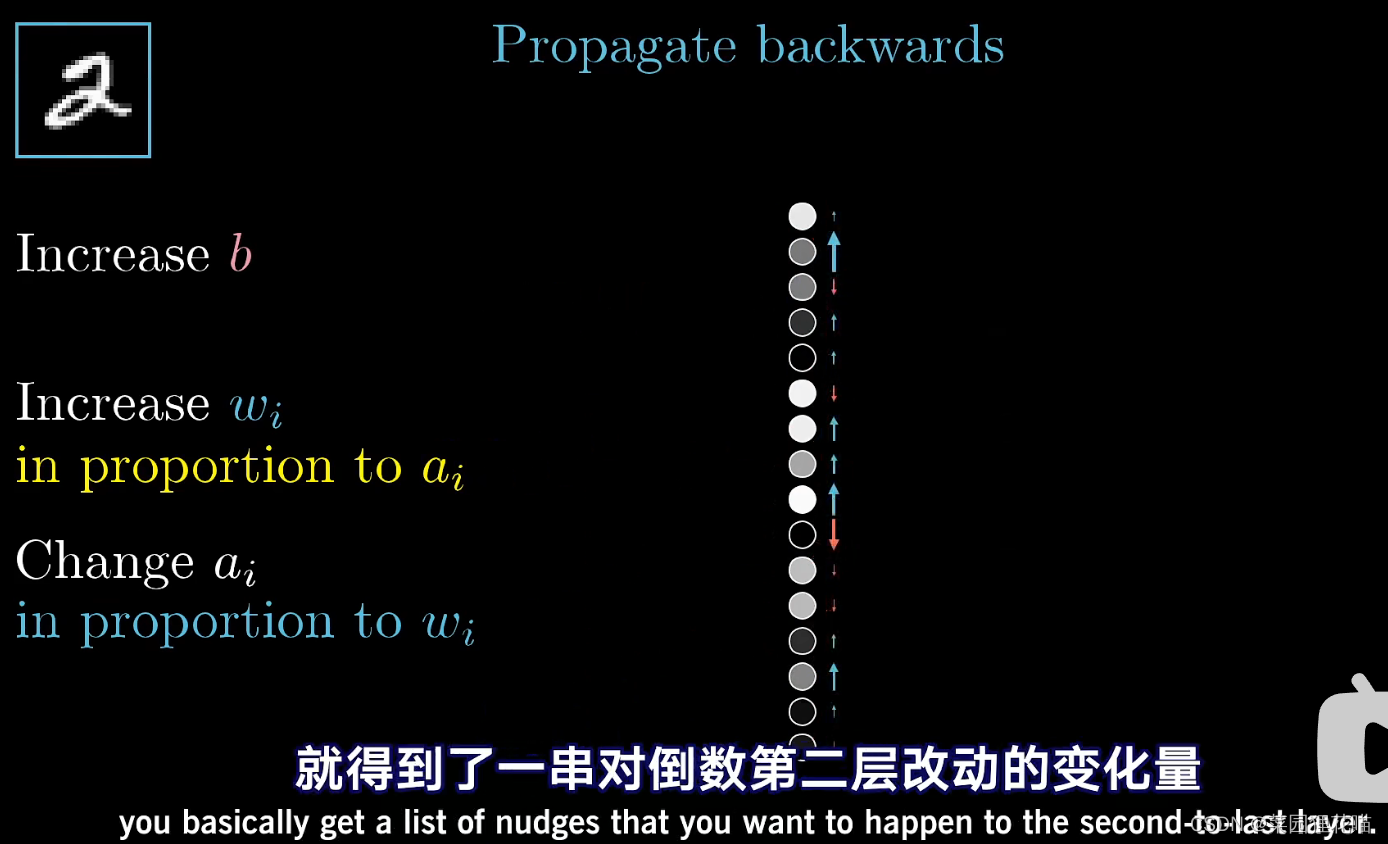
然后就重复这个过程,改变影响倒数第二层神经元激活值的相关参数,从后一层到前一层,循环,直到第一层。
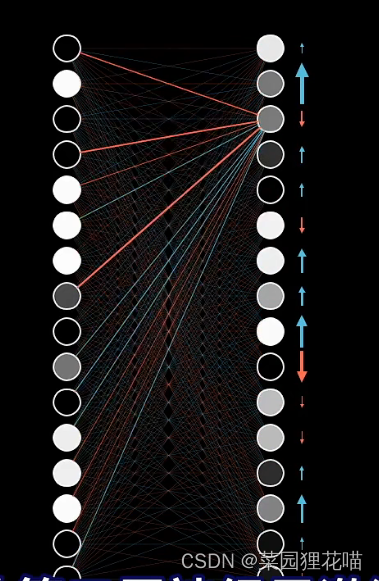
如果对所有的训练样本都过一遍反向传播,记录下每个样本想怎样修改权重和偏置,最后再取一个平均值。

这里一系列的权重偏置的平均微调大小,不严格地说就是代价函数的负梯度,至少是其标量的倍数。这里的不严格指的是还没有准确地解释如何量化这些微调。

实际操作中,如果梯度下降的每一步都用上每一个训练样本来计算的话,那么花的时间就太长了。所以一般会将训练样本打乱,然后分成很多组minibatch,每个minibatch比如说有100个训练样本,然后计算出这个minibatch下降的一步,这不是代价函数真正的梯度,然而每个minibatch都会给你一个不错的近似,而且更重要的计算量会减轻不少(这其实就是MBGD小批量随机梯度下降)
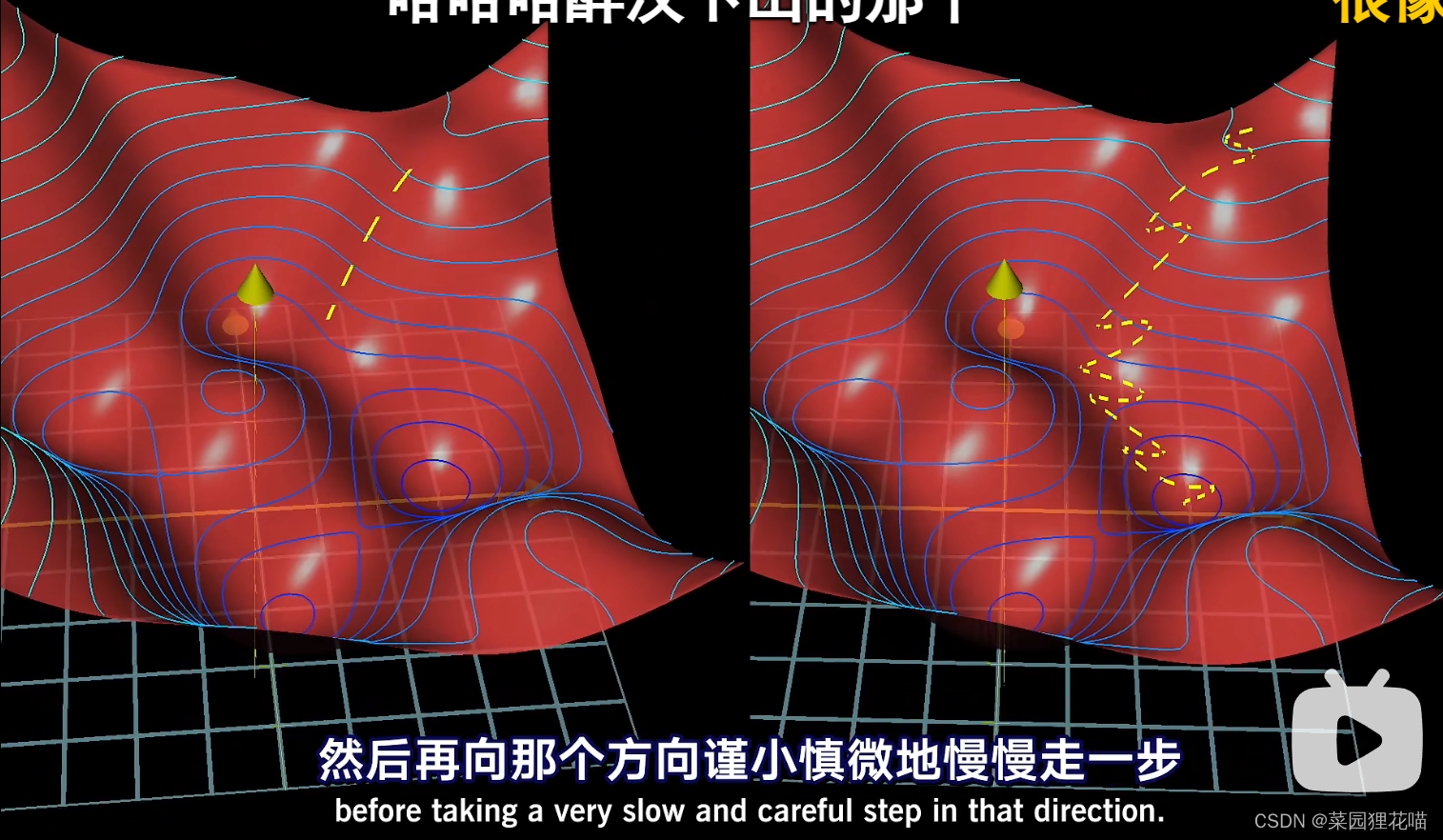
如果把网络沿代价函数的表面下山的路径画出来的话,它看上去有点像醉汉漫无目的地遛下山,但起码步伐很快(右)。而不像是细致入微的人,踏步之前先准确地算好下坡的方向,然后再向那个方向谨小慎微地慢慢走一步
小结:
反向传播算法算的是单个训练样本想怎样修改权重与偏置,不仅是说每个参数应该变大还是变小,还包括了这些变化的比例是多大才能最快地降低代价。真正的梯度下降得对好几万个训练范例都这么操作,然后对这些变化值取平均,但这样计算太慢了,所以会先把所有的样本分到各个minibatch中去,计算一个minibatch来作为梯度下降的一步,计算每个minibatch的梯度,调整参数,不断循环,最终就会收敛到代价函数的一个局部最小值上。
所以就应该能看懂反向传播的实现代码了。
视频中别人写的实现代码可以参考:
github:https://github.com/ZHE2018/network
