特征值/特征向量的计算
首先如公式所示
A
υ
=
λ
υ
A\upsilon =\lambda \upsilon
Aυ=λυ
如果向量
υ
\upsilon
υ和
λ
\lambda
λ满足以上公式,那么他们可以分别叫做矩阵A的特征向量和特征值,至于特征向量和特征值的物理含义是什么,可以参考b站3blue1brown的视频(天花板级讲解)
特征值分解(EVD)
同样摆出特征值分解的公式:
A
=
Q
∑
Q
?
1
A=Q\sum Q^{-1}
A=Q∑Q?1
特征值分解表示:如果A的方阵,那么可以分解为如上的右面所示的表达,其计算过程如下
1.求出所有特征值和对应特征向量;
2.所有特征向量构成的矩阵就是Q矩阵;
3.
∑
\sum
∑就是所有特征值构成的对角矩阵。
问题1:那如果A是不是方阵的时候该怎么解决呢?这就引来了奇异值分解了
奇异值分解(SVD)
奇异值分解的公式如下
A
=
U
∑
V
?
T
A=U\sum V^{-T}
A=U∑V?T
这时的A就可以是任何
m
×
n
m\times n
m×n的矩阵了,其中分解后的U矩阵是
m
×
m
m\times m
m×m的方阵,而V矩阵是
n
×
n
n\times n
n×n的方阵,
∑
\sum
∑ 择是
m
×
n
m\times n
m×n的对角矩阵。
具体计算步骤如下:
1.求
A
A
?
T
AA^{-T}
AA?T 的特征值和特征向量,所有特征向量单位化后构成了U矩阵
2.求
A
?
T
A
A^{-T} A
A?TA 的特征值和特征向量,所有特征向量单位化后构成了V矩阵
3.求
A
A
?
T
AA^{-T}
AA?T 和
A
?
T
A
A^{-T} A
A?TA 的特征值的平方根,构成的斜对角矩阵为 $\sum $
PCA(主成分分析)
PCA是做数据降维的一种方法,其原理就是寻找一组能够最大限度表征原始信息的向量作为基。其具体计算过程如下:
对于要进行降维数据集A
1.去平均值(即去中心化),即每一位特征减去各自的平均值。
2.计算协方差矩阵
1
n
A
A
?
T
\frac{1}{n} AA^{-T}
n1?AA?T
3.计算协方差矩阵的特征值和特征向量
4.对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P
5.所以降维后的数据X的表达为
Y
=
P
X
Y = PX
Y=PX。
注:可以看得出来,PCA只是奇异值分解SVD中的一个子问题,因为其只好比只是求解了右半边的奇异矩阵V。就完成了对列的降维压缩。而在奇异值分解SVD中,还多了一步左奇异矩阵分解得到U,完成对行的压缩,可以看出SVD的数据降维是通过行和列上同时进行的,压缩得更狠。
问题2:在以上的奇异值分解中,要完成特征值特征向量的求解,首要前提是这个矩阵本身要稠密,但是现实的用户的打分(不一定打分)矩阵一定是稀疏的,就好比下图所示
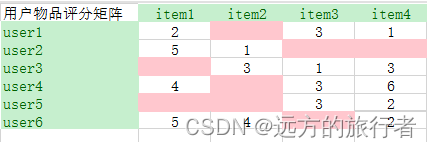
那这个问题该如何解决呢,这就引出了一个伪SVD,也称为Funk SVD
Funk SVD
Funk SVD本质上就是把直接求解矩阵问题转换为最优化问题,具体的loss公式如下
l
o
s
s
=
(
y
?
U
∑
V
)
2
loss = \left ( y-U\sum V \right )^2
loss=(y?U∑V)2
其中y为用户对物品的实际打分,
u
v
uv
uv和
∑
\sum
∑ 就是三个矩阵,具体含义可不用纠结,到后面再纠结。在求解的时候,先初始化三个矩阵,然后对有打分的位置求loss,没有打分的地方可以忽略,最终依旧可以求得三个矩阵,依旧可以计算出所有打分。
LFM
在Funk SVD中,需要求解三个矩阵,但是在实际的工程中,如果是基于一个用户打分矩阵进行分解的化,显然是分解为两个矩阵更好解释一些,一个为用户矩阵,一个为物品矩阵,对应行列相乘就是对应的打分情况,所以考虑讲
∑
\sum
∑ 融入到
u
v
uv
uv中,具体如下:
l
o
s
s
=
∑
(
y
?
U
V
)
2
loss = \sum \left ( y-UV \right )^2
loss=∑(y?UV)2
这就是LFM隐语义模型,其他的计算原理和Funk SVD是一样的。
ALS
在LFM求解过程中,肯定是用梯度下降法进行参数更新,但是这里有俩矩阵,那每次更新是更新 u u u矩阵还是 v v v矩阵,还是两个都一起更新吗?这时候就引出了ALS,ALS全称叫交替最小二乘,他的操作是交替着更新矩阵,这一步固定 v v v矩阵更新 u u u矩阵,下一步固定 u u u矩阵,更新 v v v矩阵,就这么交替更新。
注:在隐语义模型中,这个隐语义可以理解为就是那个矩阵维度k,这个k如何选择是很巧妙的,诸如在用户的行为打分矩阵的分解中,这个k就好比是用户的爱好,你觉得用户有多少爱好,就可以设置多大的k。
Neural CF(NCF)
到了深度学习发展的阶段,NCF在LFM的基础上进行了扩展,在矩阵的求解过程中,不再是通过点乘来进行学习,而是直接将用户矩阵和物品矩阵送入到MLP中,进行充分的卷积来代替点乘,它的好处在于代替点乘的同时,可以对多个特征进行深度交叉。
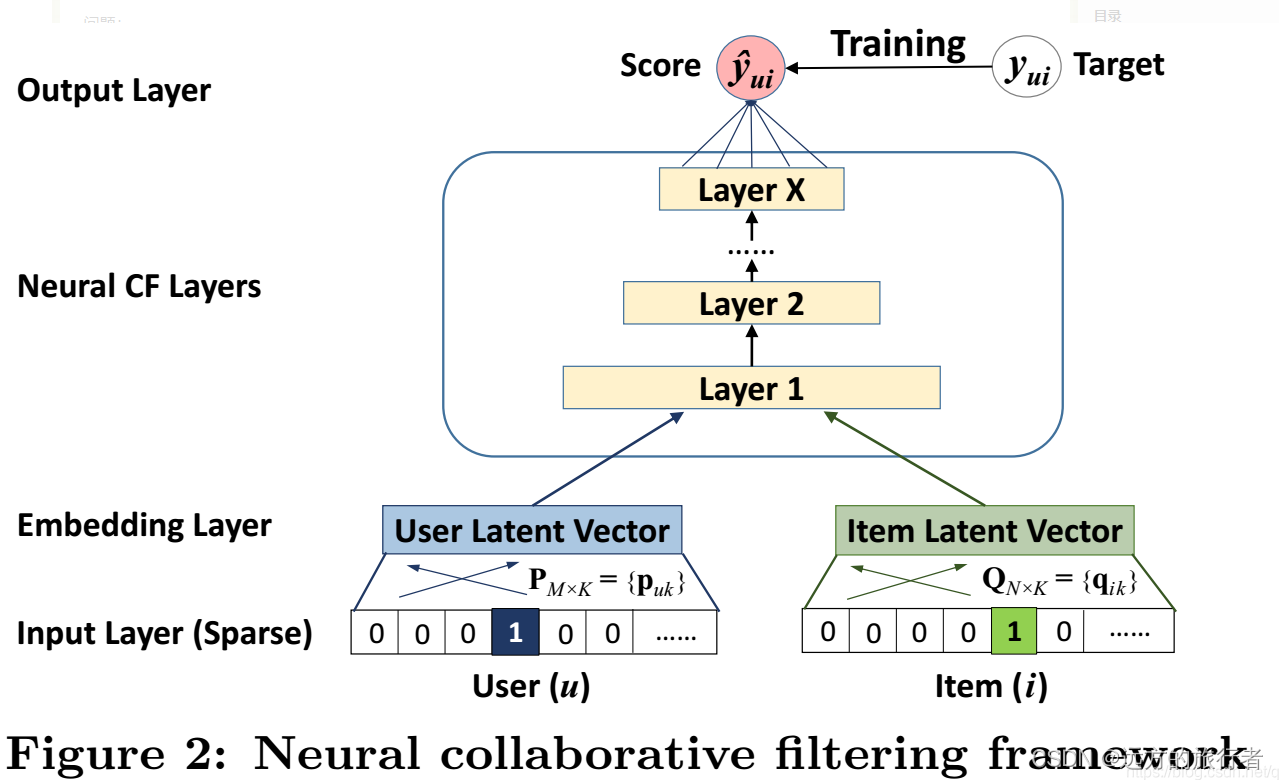
但是这有一个隐患在里面,这种充分的特征交叉之后,可能会损失原来的信息,所以为此,又出来了个GMF
GMF
它的本质是重新加入两个用户矩阵和物品矩阵的点乘,不对其进行卷积,保留原来的信息。
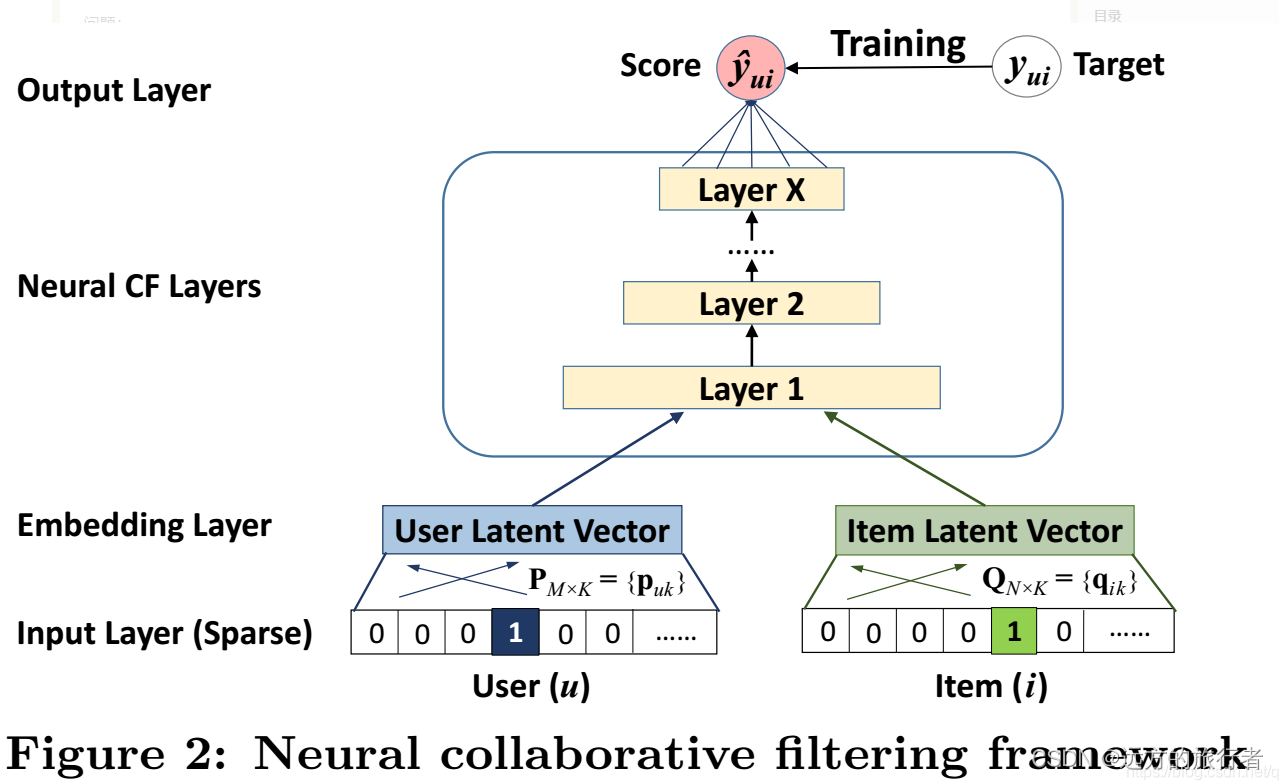
这就是矩阵分解的一个发展历程,具体实现有空再写吧。
