[人工智能]torch.nn.Conv2d介绍

卷积的计算流程

• N 是 batch_size
• C 是 channel，就是输入的维度，我们也可以认为是层数
• H 是一层 map 的高
• W 是一层 map 的宽

通俗点说，输出的每一层由一个卷积核负责，这个卷积核对输入的所有特征值进行卷积操作（对应位置点乘再相加），并求和

计算方式如下图所示：

• 因为 N 是 batch，所以输入和输出的 N 是对应的，我们可以不用关注
• $weight(C_{outj},k)$ 就代表得到第 $c_{outj}$ 层map 时在输入的第 k 层上使用的卷积核，就是上图中的蓝色小方块
• $input(N_i,k)$ 对应的就是输入的第 k 个 map
• 求和就是遍历所有输入的 feature map，从 0 到 $C_i?1$，一共 $C_i$ 个，就是输入的 map 的层数
• 我们固定$C_{outj}$，通过滑动蓝色小方块，我们进行上面的操作，就能得到一层输出 map，就是蓝色大方块
• 如果输入维度是 1，卷积过程如下所示
  

这里输入维度是3，卷积过程如下所示，一个卷积核是三个黄色块，一个黄色块对一个维度进行卷积，三个黄色块是不一样的。一个卷积核的参数量为 3*3*3 + 1(bias)

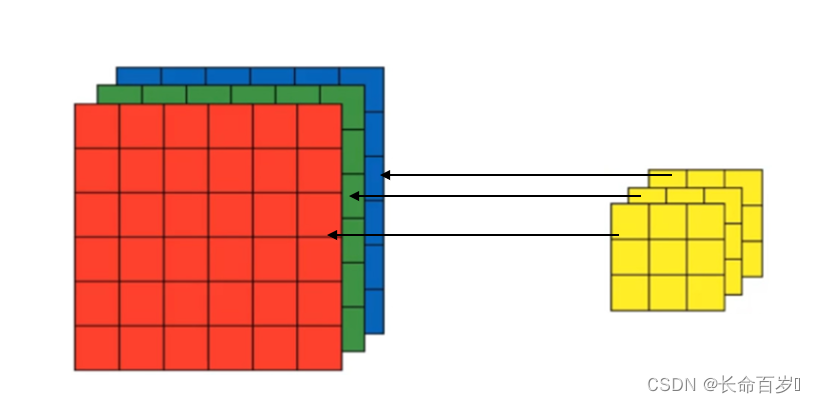
之后更换卷积核，不断变化 $C_{outj}$ ，我们就能得到红色大方块（下一个输出的 map），之后的一系列同理

一个卷积核的维度是 kernel_size[0] * kernel_size[1] * 输入维度，输出的维度等于卷积核的个数，每个卷积核负责输出一个维度

常用参数介绍

• in_channels(int)：输入图像的通道数，上面的例子中，in_channels = 3
• out_channels(int)：输出的通道数
• kernel_size(int / tuple)：卷积核的大小，就是上面蓝色和红色小方块的大小
• stride(int / tuple, optional)：步长，就是卷积核一次移动几个像素（默认是 1）
• padding(int / tuple / str, optional)：对四个方向都加 pad，默认是 0
• padding_mode(str, optional)：'zeros', 'reflect', 'replicate' or 'circular'. Default: zeros
• bias(bool, optional)：默认为 True,为输出增加可学习的偏置项

输入输出的尺寸

• 我们一般都默认，dilation = 1，因此，更直观的是

  $H_{out} = \frac{H_{in} + 2*padding[0]-kernel_size[0]}{stride[0]} + 1 \$

  $W_{out} = \frac{W_{in} + 2*padding[1]-kernel_size[1]}{stride[1]} + 1\$

  最好保证 $H_{out}$ 和 $W_{out}$ 都是整数

代码

m = nn.Conv2d(1, 1, 15, 1, 7)  # in_chan, out_chan, kernel_size, stride, padding
x = m(x)  # x 是输入

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖