3.5 Branch Attention
Branch attention 可以看成是一种动态的分支选择机制:要注意哪个,与多分支结构一起使用。
3.5.1 Highway networks
受长短期记忆网络的启发,Srivastava等人提出了高速公路网络,该网络采用自适应选通机制,使信息能够跨层流动,以解决训练非常深层网络的问题。
假设一个普通的神经网络由
L
L
L层组成,
H
l
(
X
)
H_{l}(X)
Hl?(X)表示第
l
l
l层的非线性变换,高速公路网络可以表示为
Y
l
=
H
l
(
X
l
)
T
l
(
X
l
)
+
X
l
(
1
?
T
l
(
X
l
)
)
T
l
(
X
)
=
σ
(
W
l
T
X
+
b
l
)
\begin{aligned} Y_{l} &=H_{l}\left(X_{l}\right) T_{l}\left(X_{l}\right)+X_{l}\left(1-T_{l}\left(X_{l}\right)\right) \\ T_{l}(X) &=\sigma\left(W_{l}^{T} X+b_{l}\right) \end{aligned}
Yl?Tl?(X)?=Hl?(Xl?)Tl?(Xl?)+Xl?(1?Tl?(Xl?))=σ(WlT?X+bl?)?
其中
T
l
(
X
)
T_{l}(X)
Tl?(X)表示调节第
l
l
l层信息流的变换门。
X
l
X_{l}
Xl?和
Y
l
Y_{l}
Yl?是第
l
l
l层的输入和输出。
门控机制和跳跃连接结构使得使用简单的梯度下降方法直接训练非常深的高速公路网络成为可能。与固定的跳过连接不同,门控机制适应输入,这有助于跨层路由信息。高速公路网络可以合并到任何 CNN 中。
3.5.2 SKNet
神经科学界的研究表明,视觉皮层神经元根据输入刺激自适应地调整其感受野 (RF) 的大小。这启发了 Li 等人提出了一种称为选择性内核(SK)卷积的自动选择操作。
SK 卷积使用三个操作实现:拆分、融合和选择。在拆分过程中,将具有不同内核大小的变换应用于特征图以获得不同大小的 RF。然后通过逐元素求和将来自所有分支的信息融合在一起以计算门向量。这用于控制来自多个分支的信息流。最后,在门向量的引导下,通过聚合所有分支的特征图来获得输出特征图。这可以表示为:
U
k
=
F
k
(
X
)
k
=
1
,
…
,
K
U
=
∑
k
=
1
K
U
k
z
=
δ
(
BN
?
(
W
GAP
?
(
U
)
)
)
s
k
(
c
)
=
e
W
k
(
c
)
z
∑
k
=
1
K
e
W
k
(
c
)
z
k
=
1
,
…
,
K
,
c
=
1
,
…
,
C
Y
=
∑
k
=
1
K
s
k
U
k
\begin{aligned} U_{k} &=F_{k}(X) \quad k=1, \ldots, K \\ U &=\sum_{k=1}^{K} U_{k} \\ z &=\delta(\operatorname{BN}(W \operatorname{GAP}(U))) \\ s_{k}^{(c)} &=\frac{e^{W_{k}^{(c)} z}}{\sum_{k=1}^{K} e^{W_{k}^{(c)} z}} \quad k=1, \ldots, K, \quad c=1, \ldots, C \\ Y &=\sum_{k=1}^{K} s_{k} U_{k} \end{aligned}
Uk?Uzsk(c)?Y?=Fk?(X)k=1,…,K=k=1∑K?Uk?=δ(BN(WGAP(U)))=∑k=1K?eWk(c)?zeWk(c)?z?k=1,…,K,c=1,…,C=k=1∑K?sk?Uk??
在这里,每个变换
F
k
F_{k}
Fk?都有一个独特的内核大小,以便为每个分支提供不同尺度的信息。为了提高效率,
F
k
F_{k}
Fk?是通过分组或深度卷积实现的,然后依次进行扩张卷积、批量归一化和 ReLU 激活。
t
(
c
)
t^{(c)}
t(c)表示向量
t
t
t的第
c
c
c个元素,或矩阵
t
t
t的第
c
c
c行。
SK 卷积使网络能够根据输入自适应地调整神经元的 RF 大小,从而以很少的计算成本显著改善结果。 SK 卷积中的门机制用于融合来自多个分支的信息。由于其轻量级设计,SK 卷积可以通过替换所有大内核卷积来应用于任何 CNN 主干。 ResNeSt也采用这种注意力机制以更通用的方式改进 CNN 主干,在ResNet和ResNeXt上取得了出色的结果。
3.5.3 CondConv
CNN 中的一个基本假设是所有卷积核都是相同的。鉴于此,增强网络表示能力的典型方法是增加其深度或宽度,这会带来显著的额外计算成本。为了更有效地增加卷积神经网络的容量,Yang 等人提出了一种新的多分支算子,称为 CondConv。
一个普通的卷积可以写成
Y
=
W
?
X
Y=W * X
Y=W?X
其中
?
*
?表示卷积。所有样本的可学习参数
W
W
W都是相同的。 CondConv 自适应地组合多个卷积核,可以写为:
Y
=
(
α
1
W
1
+
?
+
α
n
W
n
)
?
X
Y=\left(\alpha_{1} W_{1}+\cdots+\alpha_{n} W_{n}\right) * X
Y=(α1?W1?+?+αn?Wn?)?X
这里,
α
\alpha
α是一个可学习的权重向量,由下式计算
α
=
σ
(
W
r
(
GAP
?
(
X
)
)
)
\alpha=\sigma\left(W_{r}(\operatorname{GAP}(X))\right)
α=σ(Wr?(GAP(X)))
这个过程相当于多个专家的集合,如图 10 所示。
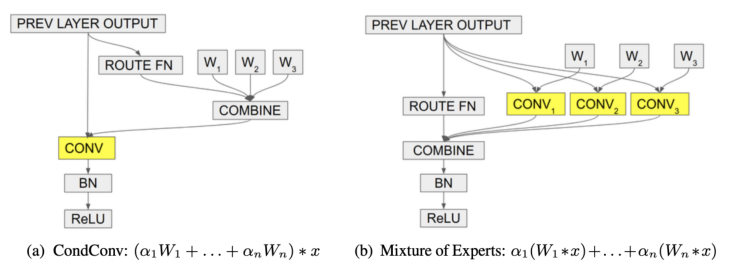
图 10. CondConv。 (a) CondConv 首先组合不同的卷积核,然后使用组合核进行卷积。 (b) 专家混合首先使用多个卷积核进行卷积,然后合并结果。虽然 (a) 和 (b) 是等价的,但 (a) 的计算成本要低得多。
CondConv 充分利用了多分支结构的优点,采用分支注意力的方法,计算成本低。它提出了一种有效提高网络能力的新方法。
3.5.4 Dynamic Convolution
轻量级 CNN 的极低计算成本限制了网络的深度和宽度,进一步降低了它们的表示能力。为了解决上述问题,Chen 等人提出了动态卷积,这是一种新颖的算子设计,它增加了表示能力,而额外的计算成本可以忽略不计,并且不会与CondConv并行改变网络的宽度或深度。
动态卷积使用
K
K
K个相同大小和输入/输出维度的并行卷积核,而不是每层一个核。与 SE 块一样,它采用挤压和激发机制来为不同的卷积核生成注意力权重。然后这些内核通过加权求和动态聚合并应用于输入特征图
X
X
X:
s
=
softmax
?
(
W
2
δ
(
W
1
GAP
?
(
X
)
)
)
?DyConv?
=
∑
i
=
1
K
s
k
Conv
?
k
Y
=
DyConv
?
(
X
)
\begin{aligned} s &=\operatorname{softmax}\left(W_{2} \delta\left(W_{1} \operatorname{GAP}(X)\right)\right) \\ \text { DyConv } &=\sum_{i=1}^{K} s_{k} \operatorname{Conv}_{k} \\ Y &=\operatorname{DyConv}(X) \end{aligned}
s?DyConv?Y?=softmax(W2?δ(W1?GAP(X)))=i=1∑K?sk?Convk?=DyConv(X)?
在这里,卷积通过卷积核的权重和偏差的总和进行组合。
与将卷积应用于特征图相比,压缩激励和加权求和的计算成本极低。因此,动态卷积提供了一种有效的操作来提高表示能力,并且可以很容易地用作任何卷积的替代品。
