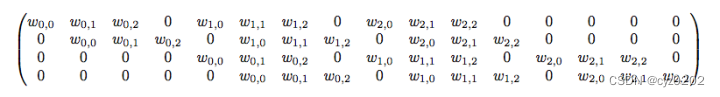1. 空洞卷积
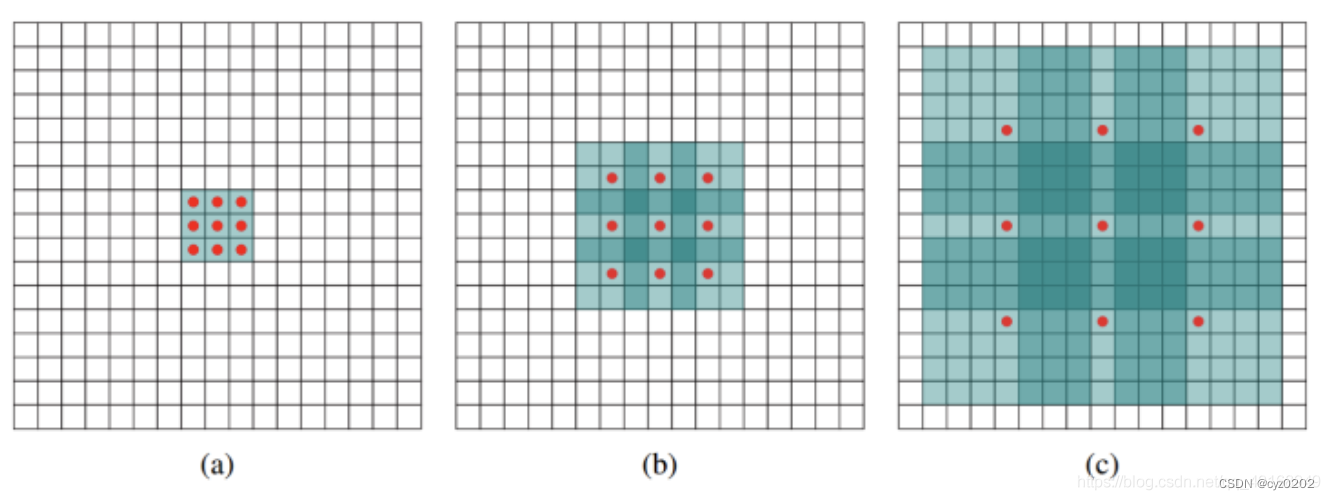
- 1.1 如上图所示,空洞卷积是为了增加感受野(pooling虽然能增加感受野,但是容易丢失原有信息);
- 1.2 实现原理:
- 图a为普通3*3卷积(注:该卷积也可视为空洞率=1的空洞卷积,见以下说明);
- 图b是空洞率=2的空洞卷积,即向原有卷积核前中后都插入一个权重为0的格子;此时卷积核变为77,但是有值的格子还是只有原来的33;
- 图c是空洞率=4的空洞卷积,情况如图b;
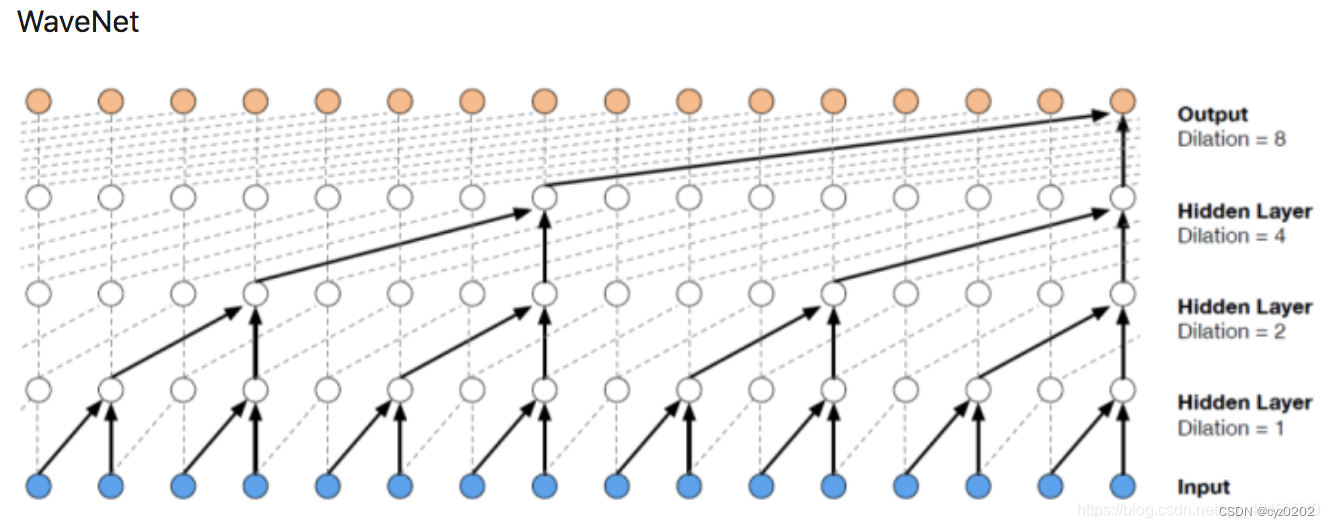
- 1.3 空洞卷积的应用:如下是在语音里的应用(Dilation=2即空洞率为2)
 - 1.4 补充:pooling容易丢失信息
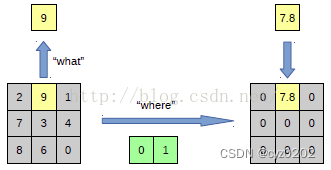
2. 转置卷积
- 转置卷积是用来将卷积后的输出还原到输入的,但是只是shape上的还原,不是真正的完全还原,以下说明;
- 假设我们的输入
A
(
s
h
a
p
e
=
4
?
4
)
A(shape=4*4)
A(shape=4?4),卷积核
B
(
s
h
a
p
e
=
3
?
3
)
B(shape=3*3)
B(shape=3?3),普通卷积(no padding & stride=1)后得到形状为2*2的输出;
- 实际计算该过程时,有一种方式是采用矩阵的形式进行处理的(还有其他更高效的方式);具体是对A reshape得到1*16,B根据计算需要,会变为16*4的矩阵(称为Toeplitz matrix,简记为
T
T
T矩阵),那么
A
?
T
=
C
=
1
?
4
A*T=C=1*4
A?T=C=1?4,reshape C的形状为2*2
- 如下示例3x3卷积核变成的T矩阵(注意下图是转置后的,即4x16)是什么样的,感兴趣的读者可以自行推导一下该矩阵方式计算的结果是否和概念上的普通卷积结果一致;
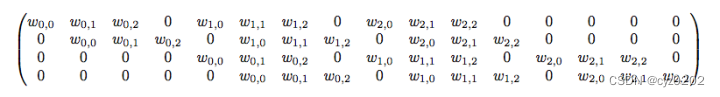 - 采用矩阵形式计算卷积,那么还原的过程就很自然了。输出的shape为2*2,将之reshape为 1*4,再与T矩阵的转置(4*16)进行矩阵计算,即可得到1*16,再reshape为4*4,就和原始输入A有一样的shape了;
- 显然上一步不保证能得到真正的原始输入A;因为上述卷积的矩阵计算是
A
?
T
=
C
A*T=C
A?T=C,此时对等式两边都乘以
T
(
s
h
a
p
e
=
16
?
4
)
T(shape=16*4)
T(shape=16?4)矩阵的转置
T
′
(
s
h
a
p
e
=
4
?
16
)
T'(shape=4*16)
T′(shape=4?16),变为
A
?
T
?
T
′
=
C
?
T
′
A*T*T'=C*T'
A?T?T′=C?T′,如果
A
?
T
?
T
′
=
C
?
T
′
=
A
A*T*T'=C*T'=A
A?T?T′=C?T′=A成立,那么要求
T
?
T
′
=
I
T*T'=I
T?T′=I,
I
I
I为单位矩阵,显然不一定成立;
3. 反卷积
- 举例如下
普通卷积(no padding & stride=1)

对应反卷积(注意需要扩充)
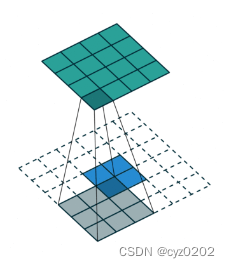
普通卷积(padding & stride=2),

对应反卷积(注意需要扩充)
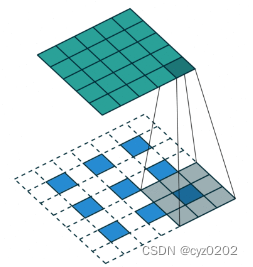 - 从最后一张图,可以看到反卷积需要对输入进行扩充(填充空洞);空洞卷积则是对卷积核进行扩充;从效果上看,反卷积减少了卷积核的视野,空洞卷积则增强了卷积核的视野;
|