[人工智能]【pytorch】（十一）循环神经网络（RNN）

循环神经网络（RNN）

对于循环神经网络，网上的讲解都是按照时间线展开进行的：

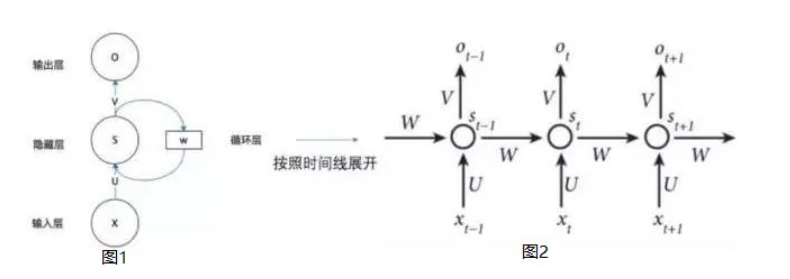
图片来自网络

我个人觉得这样复杂化了。然后，又有人用以下图片来解释这种复杂化：

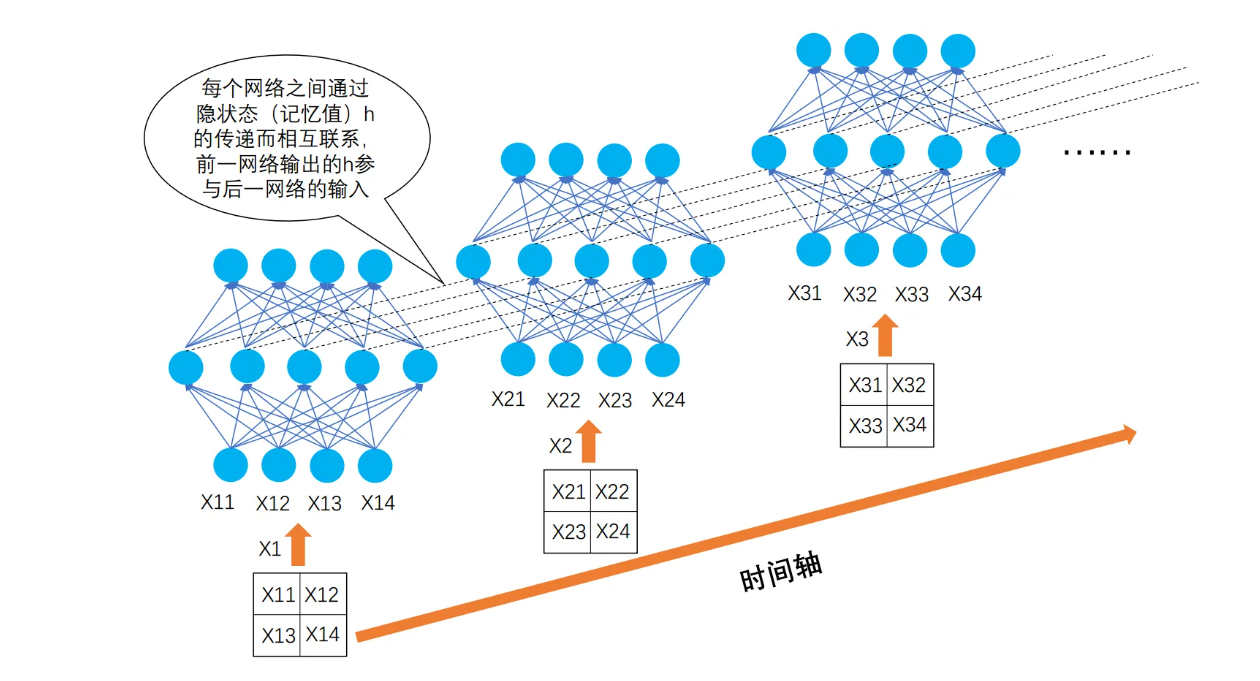
图片来自网络

看起来挺酷。

其实，循环神经网络没那么复杂。下面，本文将以“序列动，网络不动”的角度展示循环神经网络的前向传播，并有前馈神经网络作为对照。然后，同样以“序列动，网络不动”的角度清晰地展示双向循环神经网络的前向传播。

RNN与前馈神经网络对比

	循环神经网络（RNN）	前馈神经网络
网络简图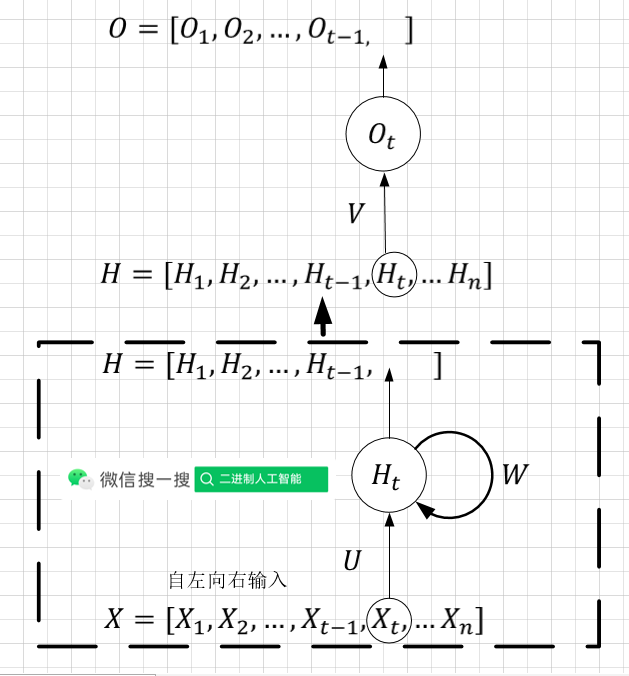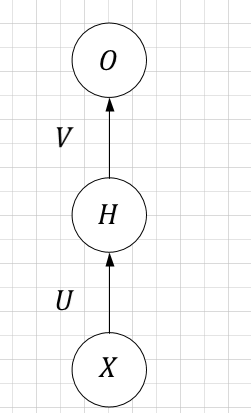
输入	时间序列：$X=[X_1.X_2,X_3,...,X_{t?1},X_t...,X_n]$	非时间序列：$X$

前向传播（不考虑偏置$b$，$f$为激活函数）
（1）前馈神经网络:

$$O=f(VH)=f(Vf(UX))$$

（2）循环神经网络:

$X$的元素依次输入，计算
$$\begin{array}{rl}{H}_1& =f(U{X}_1+W{H}_0),H_0常设为0\\ H_2& =f(U{X}_2+W{H}_1)=f(U{X}_2+WU{X}_1)\\ H_3& =f(U{X}_3+W{H}_2)=f(U{X}_3+WU(U{X}_2+W{H}_1)\\ & =f(U{X}_3+WU(U{X}_2+WU{X}_1))\\ ...& \\ H_t& =f(U{X}_t+W{H}_{t?1})\\ ...& \end{array}$$
得到：
$$H=[H_1.H_2,H_3,...,H_{t?1},H_t...,H_n]$$
后接一个前馈网络：
$$\begin{array}{rl}{O}_1& =f(V{H}_1)\\ O_2& =f(V{H}_2)\\ O_3& =f(V{H}_3)\\ ...& \\ O_t& =f(V{H}_t)\\ ...& \end{array}$$
输出：
$$O=[O_1.O_2,O_3,...,O_{t?1},O_t...,O_n]$$

就这么简单，下面举两个例子。

Pytorch实现

序列到类别

将图像(28x28)自上而下视为一个时间序列

$$X=[X_1.X_2,X_3,...,X_{t?1},X_t...,X_{28}]$$

其中$X_t$为图像第$t$行的像素。

序列输入循环神经网络，输出
$$H=[H_1.H_2,H_3,...,H_{t?1},H_t...,H_{28}]$$

取其中的$H_{28}$输入前馈神经网络，得到分类预测值。

import torch
import torch.nn as nn
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
import matplotlib

torch.manual_seed(1)
matplotlib.rcParams['font.family'] = 'SimHei'
matplotlib.rcParams['axes.unicode_minus'] = False
plt.rcParams['figure.dpi'] = 150
device = 'cuda' if torch.cuda.is_available() else 'cpu'
print(device)


class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, n_class):
        super(RNN, self).__init__()
        self.num_layers = num_layers
        self.hidden_size = hidden_size
        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=num_layers,
            batch_first=True,
            nonlinearity='relu'
        )
        self.linear = nn.Linear(hidden_size, n_class)

    def forward(self, x):
        h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(device)
        out, hn = self.rnn(x, h0)
        out = out[:, -1, :]  # = hn
        out = self.linear(out)
        return out


def test(dataset_test, model):
    correct = 0
    total_num = len(dataset_test)
    test_loader = DataLoader(dataset=dataset_test, batch_size=64, shuffle=False)
    for (test_images, test_labels) in test_loader:
        test_images = test_images.squeeze(1)
        test_images = test_images.to(device)
        test_labels = test_labels.to(device)
        predicted = model(test_images)
        _, predicted = torch.max(predicted, 1)
        correct += torch.sum(predicted == test_labels)
    accuracy = correct.item() / total_num
    print('测试准确率:{:.5}'.format(accuracy))
    return accuracy


def train():
    accuracy_list = []
    learning_rate = 0.001
    batch_size = 128

    model = RNN(input_size=28, hidden_size=128, num_layers=1, n_class=10)  # 图片大小是28x28
    model = model.to(device)

    dataset_train = datasets.MNIST(root='./mnist', transform=transforms.ToTensor(), train=True, download=False)
    dataset_test = datasets.MNIST(root='./mnist', transform=transforms.ToTensor(), train=False, download=False)

    train_loader = DataLoader(dataset=dataset_train, batch_size=batch_size, shuffle=True)

    optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
    loss_f = nn.CrossEntropyLoss()
    for epoch in range(20):
        model.train()
        for step, (train_images, train_labels) in enumerate(train_loader):
            train_images = train_images.squeeze(1)  # [64, 1, 28, 28]->[64, 28, 28]
            train_images = train_images.to(device)
            train_labels = train_labels.to(device)
            predicted = model(train_images)
            loss = loss_f(predicted, train_labels)

            # 反向传播，更新参数
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            if (step % 100 == 0):
                print('epoch:{},step:{},loss:{}'.format(epoch + 1, step, loss.item()))

        model.eval()
        accuracy = test(dataset_test, model)
        accuracy_list.append(accuracy)
    plt.plot(accuracy_list)
    plt.title('准确率')
    plt.show()


if __name__ == '__main__':
    train()

结果：

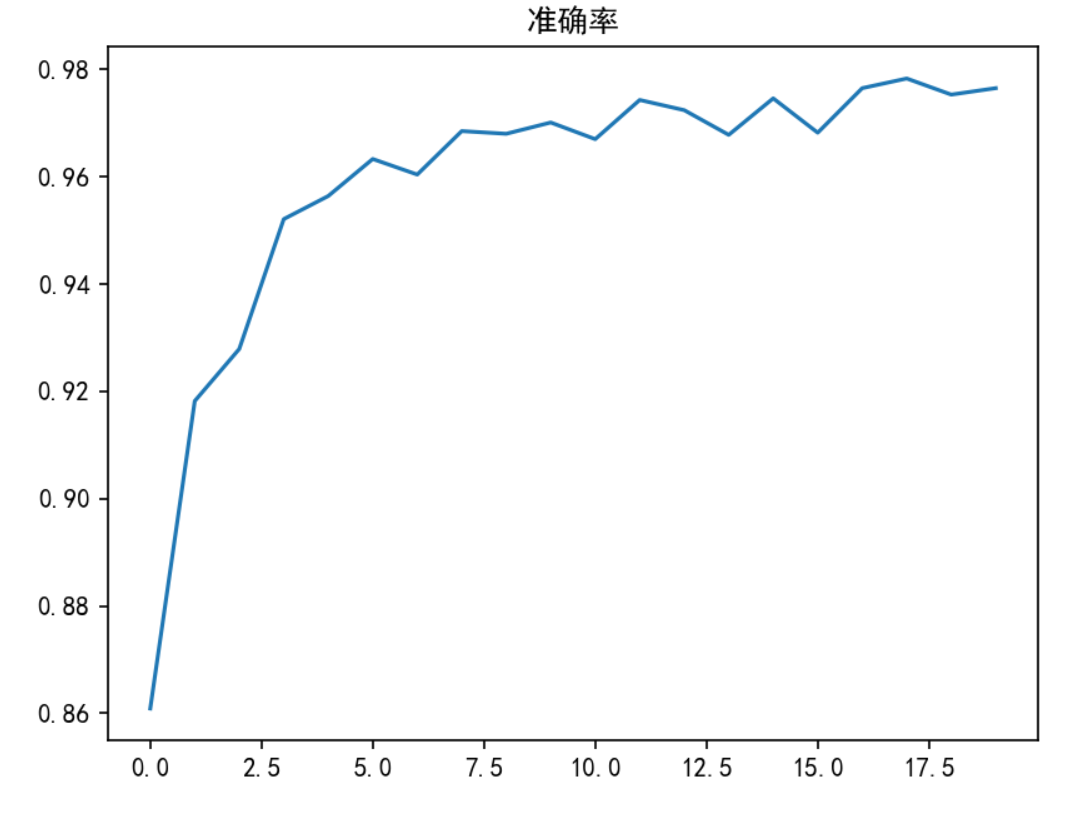
序列到序列

训练：
正弦波预测。有一正弦波序列$S=[S_1.S_2,S_3,...,S_{t?1},S_t...,S_n]$。令
$$X=[S_1.S_2,S_3,...,S_{t?1},S_t...,S_{n?1}]$$

$$Y=[S_2,S_3,...,S_{t?1},S_t...,S_n]$$

$X$输入网络，输出
$$H=[H_1.H_2,H_3,...,H_{t?1},H_t...,H_{n?1}]$$
输入前馈网络，得到输出：
$$O=[O_1.O_2,O_3,...,O_{t?1},O_t...,O_{n?1}]$$

最小化$O$与$Y$之间的误差。

测试：输入[0]，输出正弦波序列

import torch
import torch.nn as nn
import numpy as np
import torch.optim as optim
from matplotlib import pyplot as plt
import matplotlib

torch.manual_seed(1)
np.random.seed(1)
matplotlib.rcParams['font.family'] = 'SimHei'
matplotlib.rcParams['axes.unicode_minus'] = False
device = 'cuda' if torch.cuda.is_available() else 'cpu'
print(device)


class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, output_size):
        super(RNN, self).__init__()
        self.num_layers = num_layers
        self.hidden_size = hidden_size

        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=num_layers,
            batch_first=True,
            bidirectional=False,
        )
        self.linear = nn.Linear(hidden_size, output_size)

    def forward(self, inputs, h0):
        # x: [batch_size, seq_len, input_size]
        # h0: [num_layers, batch_size, hidden_size]
        outputs, hn = self.rnn(inputs, h0)
        # out: [batch_size, seq_len, hidden_size]
        # hn: [num_layers, batch_size, hidden_size]

        # [batch, seq_len, hidden_size] => [batch * seq_len, hidden_size]
        outputs = outputs.view(-1, self.hidden_size)

        # [batch_size * seq_len, hidden_size] => [batch_size * seq_len, output_size]
        outputs = self.linear(outputs)

        # [batch_size * seq_len, output_size] => [batch_size, seq_len, output_size]
        outputs = outputs.view(inputs.size())

        return outputs, hn


def test(model, seq_len, h0):
    input = torch.tensor(0, dtype=torch.float)
    predictions = []
    for _ in range(seq_len):
        input = input.view(1, 1, 1)
        prediction, hn = model(input, h0)
        input = prediction
        h0 = hn
        predictions.append(prediction.detach().numpy().ravel()[0])
    # 画图
    time_steps = np.linspace(0, 10, seq_len)
    data = np.sin(time_steps)
    a, = plt.plot(time_steps, data, color='b')
    b = plt.scatter(time_steps[0], 0, color='black', s=10)
    c = plt.scatter(time_steps[1:], predictions[1:], color='red', s=10)
    plt.legend([a, b, c], ['正弦波', '输入', '预测'])
    plt.show()


def train():
    seq_len = 100
    input_size = 1
    hidden_size = 16
    output_size = 1
    num_layers = 1
    lr = 0.01

    model = RNN(input_size, hidden_size, num_layers, output_size)
    loss_function = nn.MSELoss()
    optimizer = optim.Adam(model.parameters(), lr)
    h0 = torch.zeros(num_layers, input_size, hidden_size)

    for i in range(3000):
        # 训练的数据:batch_size=1
        time_steps = np.linspace(0, 10, seq_len + 1)
        data = np.sin(time_steps)
        data = data.reshape(seq_len + 1, 1)
        # 去掉最后一个元素，作为输入
        inputs = torch.tensor(data[:-1]).float().view(1, seq_len, 1)
        # 去掉第一个元素，作为目标值 [batch_size, seq_len, input_size]
        target = torch.tensor(data[1:]).float().view(1, seq_len, 1)

        output, hn = model(inputs, h0)

        # 与上一个批次的计算图分离 https://www.cnblogs.com/catnofishing/p/13287322.html
        hn.detach()

        loss = loss_function(output, target)
        model.zero_grad()
        loss.backward()
        optimizer.step()

        if i % 100 == 0:
            print("迭代次数: {} loss {}".format(i, loss.item()))

    test(model, seq_len, h0)


if __name__ == '__main__':
    train()

结果：

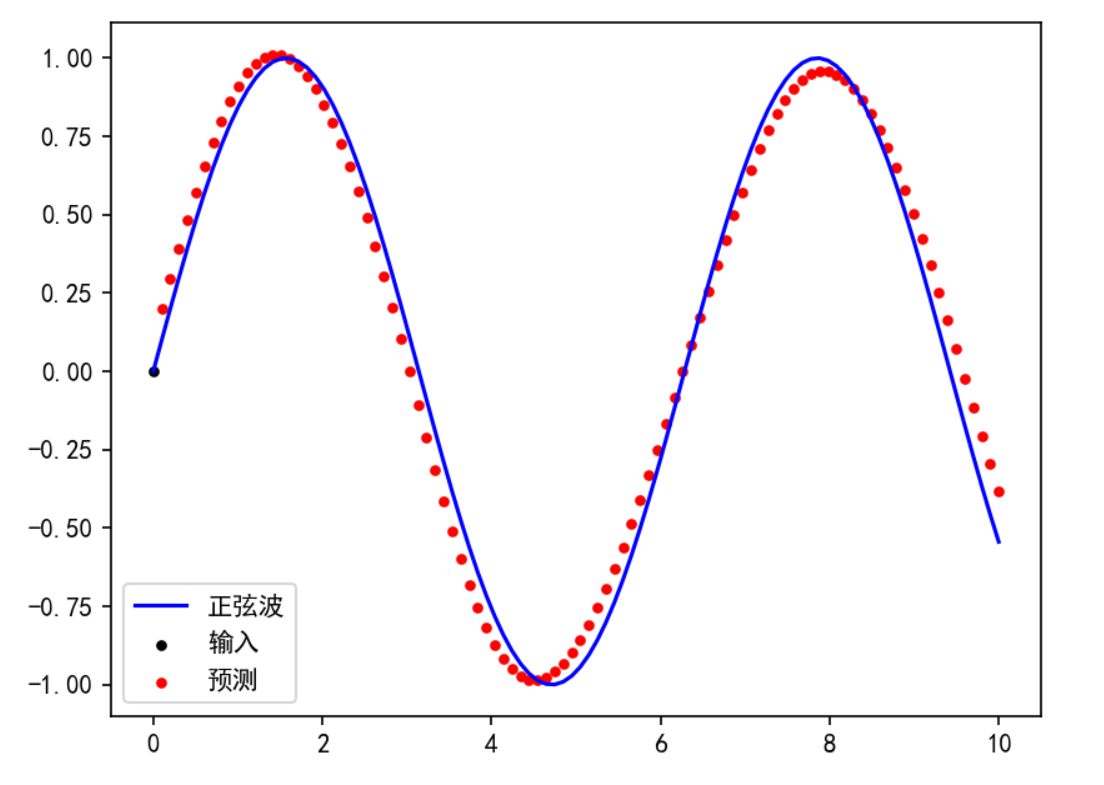
双向RNN

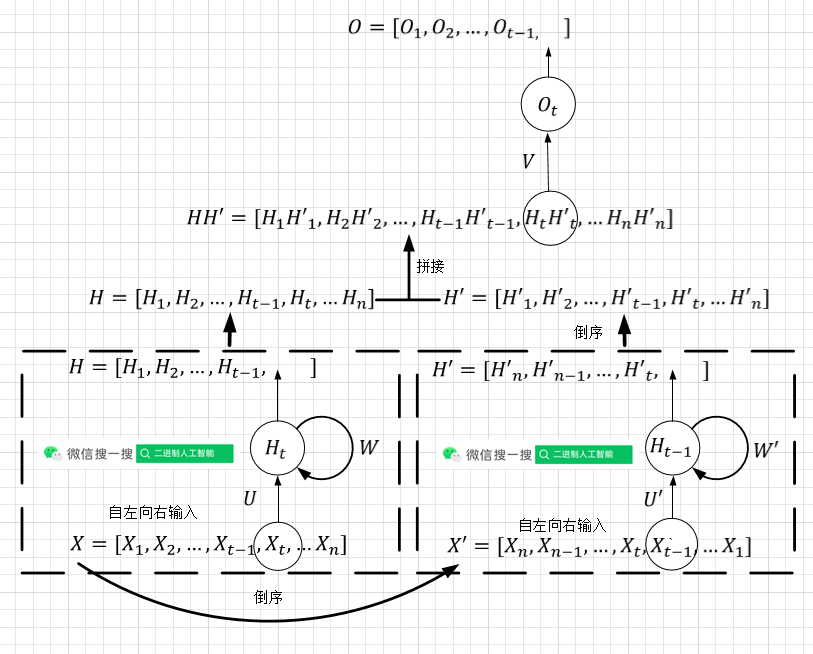
原序列：
$$\begin{array}{rl}{H}_1& =f(U{X}_1+W{H}_0)，H_0常设为0\\ H_2& =f(U{X}_2+W{H}_1))=f(U{X}_2+WU{X}_1)\\ H_3& =f(U{X}_3+W{H}_2))=f(U{X}_3+WU(U{X}_2+W{H}_1))\\ & =f(U{X}_3+WU(U{X}_2+WU{X}_1))\\ ...& \\ H_t& =f(U{X}_t+W{H}_{t?1})\\ ...& \end{array}$$
得到：
$$H=[H_1.H_2,H_3,...,H_{t?1},H_t...,H_T]$$
倒序序列：
$$\begin{array}{rl}{H}_n^{\prime }& =f(U^{\prime }{X}_n+W^{\prime }{H}_{n+1}^{\prime })，H_{n+1}^{\prime }常设为0\\ H_{n?1}^{\prime }& =f(U^{\prime }{X}_{n?1}+W{H}_n^{\prime }))=f(U^{\prime }{X}_{n?1}+W^{\prime }{U}^{\prime }{X}_n)\\ H_{n?2}& =f(U^{\prime }{X}_{n?2}+W^{\prime }{H}_{n?1}))=f(U^{\prime }{X}_{n?2}+W^{\prime }{U}^{\prime }(U^{\prime }{X}_{n?1}+W^{\prime }{H}_{{}_n}))\\ & =f(U^{\prime }{X}_{n?2}+W^{\prime }{U}^{\prime }(U^{\prime }{X}_{n?1}+W^{\prime }{U}^{\prime }{X}_n))\\ ...& \\ H_t^{\prime }& =f(U^{\prime }{X}_t+W^{\prime }{H}_{t+1})\\ ...& \end{array}$$
得到：
$$H^{\prime }=[H_1^{\prime }.H_2^{\prime },H_3^{\prime },...,H_{t?1}^{\prime },H_t^{\prime }...,H_T^{\prime }]$$

拼接：
$$H{H}^{\prime }=\left[H_1{H}_1^{\prime },H_2{H}_2^{\prime },\dots ,H_{t?1}{H}_{t?1}^{\prime },H_t{H}^{\prime }{}_t,\dots H_n{H}_n^{\prime }\right]$$

后接一个前馈网络：
$$\begin{array}{rl}{O}_1& =f(V[H_1{H}_1^{\prime }])\\ O_2& =f(V[H_2{H}_2^{\prime }])\\ O_3& =f(V[H_3{H}_3^{\prime }])\\ ...& \\ O_t& =f(V[H_t{H}_t^{\prime })]\\ ...& \end{array}$$
输出：
$$O=[O_1.O_2,O_3,...,O_{t?1},O_t...,O_T]$$

Pytorch实现：序列到类别

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, n_class):
        super(RNN, self).__init__()
        self.num_layers = num_layers
        self.hidden_size = hidden_size
        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=num_layers,
            batch_first=True,
            bidirectional=True,
            nonlinearity='relu'
        )
        self.linear = nn.Linear(2*hidden_size, n_class)

    def forward(self, x):
        h0 = torch.zeros(self.num_layers*2,  x.size(0), self.hidden_size).to(device)
        out, hn = self.rnn(x, h0)
        out = out[:, -1, :]  # = hn
        out = self.linear(out)
        return out

结果：

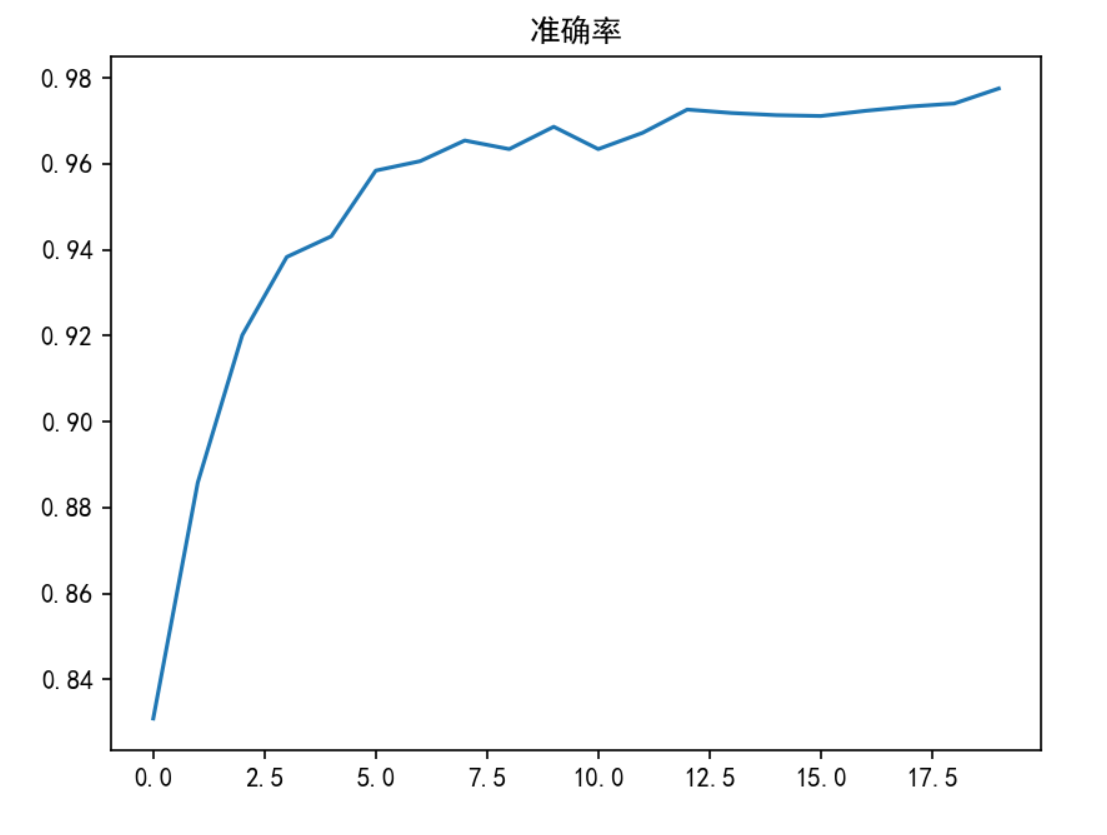
附：nn.RNN类

CLASS torch.nn.RNN(*args, **kwargs)

参数说明：

• input_size：输入序列单元$x_t$的维度。
• hidden_size：隐藏层神经元个数，或者也叫输出的维度
• num_layers：网络的层数，默认为1
• nonlinearity：激活函数，默认为tanh
• bias：是否使用偏置
• batch_first：输入数据的形式，默认是 False，形式为(seq, batch, feature)，也就是将序列长度放在第一位，batch 放在第二位。如果为True，则为(batch, seq, feature)
• dropout：dropout率, 默认为0，即不使用。如若使用将其设置成一个0-1的数字即可。
• birdirectional：是否使用两层的双向的 rnn，默认是 False

记：
$$\begin{array}{rl}N& =\text{batch?size}\\ L& =\text{?sequence?length?}\\ D& =2\text{?if?bidirectional=True?otherwise?}1\\ H_{\text{in}}& =\text{?input\_size?}\\ H_{out}& =\text{?hidden\_size?}\end{array}$$
输入：input, h_0
（1）input(输入序列)

非批量：$(L,H_{in})$

批量：如果batch_first=False，$（L,N,H_{in})$；如果batch_first=True，$（N,L,H_{in})$

（2） h_0（每一层网络的初始状态。如果未提供，则默认为零。）
非批量：$(D\times \text{num\_layers},H_{out})$

批量：$(D\times \text{num\_layers},N,H_{out})$

输出，output，hn：
（1）output:
非批量：$(L,D\times H_{out})$

批量：如果batch_first=False，$（L,N,H_{out})$；如果batch_first=True，$（N,L,H_{out})$

（2）h_n:状态
非批量：$(D\times \text{num\_layers},H_{out})$

批量：$(D\times \text{num\_layers},N,H_{out})$

权重和偏置初始化：

从均匀分布$U(?\sqrt{k},\sqrt{k})$采样，其中$k=\frac{1}{hidden\_size}$

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖