[人工智能]机器学习（19）——循环神经网络（一）

1 简介

??在本系列文章中，我有跟大家分享过神经网络中两种经典层：卷积层(CNN) 和 全连接层(FC)，这两种层的输入数据分别是：特征向量和图像(张量)，在具体实现时输入的多样本之间是相互独立的，无联系关系。而且，卷积神经网络利用数据的局部相关性和权值共享的思想大大减少了网络的参数量，非常适合于图片这种具有 空间(Spatial) 局部相关性的数据，但自然界的信号除了具有空间维度之外，还有一个 时间(Temporal) 维度。具有时间维度的数据(也称作序列数据)有以下特点：

• 不同样本之间存在相互关联；
• 模型的输出不仅 取决于当前输入，也受历史输入的影响。

因此卷积神经网络并不擅长处理此类数据，本博客要介绍的循环神经网络可以较好地解决此类问题。
??常见的序列数据有：语言、音乐、视频、股票、文字、DNA等等。

2 序列表示方法

??具有先后顺序的数据一般叫作 序列(Sequence)，比如随时间而变化的商品价格数据就是非常典型的序列。考虑某件商品 A 在 1 月到 6 月之间的价格变化趋势，我们记为一维向量：$[{\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3,{\mathbf{x}}_4,{\mathbf{x}}_5,{\mathbf{x}}_6]$，shape 为 $[6]$。如果要表示 $\mathbf{b}$ 件商品在 1 月到 6 月之间的价格变化趋势，可以记为 2 维张量：
$$\left[[{\mathbf{x}}_1^{(1)},{\mathbf{x}}_2^{(1)},?,{\mathbf{x}}_6^{(1)}],[{\mathbf{x}}_1^{(2)},{\mathbf{x}}_2^{(2)},?,{\mathbf{x}}_6^{(2)}],?,[{\mathbf{x}}_1^{(6)},{\mathbf{x}}_2^{(6)},?,{\mathbf{x}}_6^{(6)}]\right]$$
其中 $\mathbf{b}$ 表示商品的数量，张量 shape 为 $[\mathbf{b},6]$。因此，表示一个序列信号只需要一个 shape 为 $[\mathbf{b},\mathbf{s}]$ 的张量，其中 $\mathbf{b}$ 为序列数量，$\mathbf{s}$ 为一个序列的长度。但是对于很多信号并不能直接用一个标量数值表示，比如每个时间戳产生长度为 $\mathbf{n}$ 的特征向量，则需要 shape 为 $[\mathbf{b},\mathbf{s},\mathbf{n}]$ 的张量才能表示。考虑更复杂的文本数据：句子。它在每个时间戳上面产生的单词是一个字符，并不是数值，不能直接用某个标量表示。

2.1 独热表示

??对于一个含有 $\mathbf{n}$ 个单词的句子，单词的一种简单表示方法就是 One-hot 编码。以英文句子为例，假设只考虑最常用的 1 万个单词，那么每个单词就可以表示为某位为 1，其它位置为 0 且长度为 1 万的稀疏 One-hot 向量；对于中文句子，如果也只考虑最常用的 5000 个汉字，同样的方法，一个汉字可以用长度为 5000 的 One-hot 向量表示。如果只考虑 $\mathbf{n}$ 个地名单词，可以将每个地名编码为长度为 $\mathbf{n}$ 的 One-hot 向量。

??文字编码为数值的过程叫作 Word Embedding。One-hot 的编码方式实现 Word Embedding 简单直观，编码过程不需要学习和训练。在神经网络中，一般使用 词袋模型(Bag of words) 先对单词编号，如 2 表示 “I”，3 表示 “me” 等，然后再对每个进行 One-hot 编码，最后将每个词向量拼接成矩阵或者张量。但 One-hot 编码有以下缺点：

• 容易受维数灾难的困扰，尤其是将其用于深度学习算法时；
• 任何两个词都是孤立的，存在语义鸿沟词(任意两个词之间都是孤 立的，不能体现词和词之间的关系)。如：对于单词 “like”、“dislike”、“Rome”、“Paris” 来说，“like” 和 “dislike” 在语义角度就强相关，它们都表示喜欢的程度；“Rome” 和 “Paris” 同样也是强相关，他们都表示欧洲的两个地点。如果采用 One-hot 编码，得到的向量之间没有相关性。

为了克服此不足，人们提出了另一种表示方法，即分布式表示。

2.2 分布式表示

??首先要介绍一种相似度衡量方式。在自然语言处理领域，有专门的一个研究方向在探索如何学习到单词的表示向量(Word Vector)，使得语义层面的相关性能够很好地通过 Word Vector 体现出来。一个衡量词向量之间相关度的方法就是 余弦相关度(Cosine similarity)：
$$\mathbf{s}\mathbf{i}\mathbf{m}\mathbf{i}\mathbf{l}\mathbf{a}\mathbf{r}\mathbf{i}\mathbf{t}\mathbf{y}(\mathbf{a},\mathbf{b})?\mathbf{c}\mathbf{o}\mathbf{s}(\mathbf{\theta })=\frac{\mathbf{a}?\mathbf{b}}{|\mathbf{a}|?|\mathbf{b}|}$$
其中 $\mathbf{a}$ 和 $\mathbf{b}$ 代表了两个词向量。

??分布式表示最早由 Hinton 于 1986 年提出的，可以克服独热表示的缺点。 解决词汇与位置无关问题，可以通过计算向量之间的 距离(欧式距离、余弦距离等) 来体现词与词的相似性。其基本想法是直接用一个普通的向量表示 一个词，此向量为$[0.792,?0.177,?0.107,0.109,?0.542,...]$，常见维度为 50 或 100。用这种方式表示的向量，“麦克” 和 “话筒” 的距离会远远小于“ 麦克” 和 “天气” 的距离。
??词向量的分布式表示的优点是解决了词汇与位置无关问题，不足是学习过程相对复杂且受训练语料的影响很大。训练这种向量表示的方法较多，常 见的有 LSA、PLSA、LDA、Word2Vec等，其中 Word2Vec 是 Google 在 2013 年开源的一个词向量计算工具，同时也是一套生成词向量的算法方案。

2.3 Embedding 层

??在神经网络中，单词的表示向量可以直接通过训练的方式得到，我们把单词的表示层叫作 Embedding 层。Embedding 层负责把单词编码为某个词向量 $\mathbf{v}$，它接受的是采用数字编码的单词编号$\mathbf{i}$， 也就是词袋模型编码后的结果。系统总单词数量记为${\mathbf{N}}_{\mathbf{v}\mathbf{o}\mathbf{c}\mathbf{a}\mathbf{b}}$，输出长度为 $\mathbf{n}$ 的向量 $\mathbf{v}$：
$$\mathbf{v}={\mathbf{f}}_{\mathbf{\theta }}(\mathbf{i}|{\mathbf{N}}_{\mathbf{v}\mathbf{o}\mathbf{c}\mathbf{a}\mathbf{b}},\mathbf{n})$$
构建一个 shape 为 $[{\mathbf{N}}_{\mathbf{v}\mathbf{o}\mathbf{c}\mathbf{a}\mathbf{b}},\mathbf{n}]$ 的查询表对象 $\mathbf{t}\mathbf{a}\mathbf{b}\mathbf{l}\mathbf{e}$，对于任意的单词编号 $\mathbf{i}$，只需要查询到对应位置上的向量并返回即可：
$$\mathbf{v}=\mathbf{t}\mathbf{a}\mathbf{b}\mathbf{l}\mathbf{e}[\mathbf{i}]$$
在 PyTorch 中，有一个 nn.Embedding(vocab_size，n) 类，它是 Module 类的子类，这里它接受最重要的两个初始化参数：词汇量大小，每个词汇向量表示的向量维度。Embedding 类返回的是一个形状为 [每句词个数，词维度] 的矩阵。

3 一个例子

??现在我们来考虑如何处理序列信号，以文本序列为例，考虑一个句子：
$$“Ihatethisboringmovie”$$
通过 Embedding 层，可以将它转换为 shape 为 $[\mathbf{b},\mathbf{s},\mathbf{n}]$ 的张量，$\mathbf{b}$ 为句子数量，$\mathbf{s}$ 为句子长度，$\mathbf{n}$ 为词向量长度。上述句子可以表示为 shape 为$[1,5,10]$ 的张量，其中 5 代表句子单词长度，10 表示词向量长度。
??接下来以情感分类任务为例来逐步探索能够处理序列信号的网络模型。情感分类任务通过分析给出的文本序列，提炼出文本数据表达的整体语义特征，从而预测输入文本的情感类型：正面评价 或者 负面评价。从分类角度来看，情感分类问题就是一个简单的二分类问题，与图片分类不一样的是，由于输入是文本序 列，传统的卷积神经网络并不能取得很好的效果。

3.1 考虑全连接

??对于每个词向量，分别使用一个全连接层网络来提取语义特征：
$$\mathbf{o}=\mathbf{\sigma }({\mathbf{W}}_{\mathbf{t}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}_{\mathbf{t}})$$

上图中，各个单词的词向量通过 $\mathbf{s}$ 个全连接层分类网络 1 提取每个单词的特征，所有单词的特征最后合并，并通过分类网络 2 输出序列的类别概率分布，对于长度为 $\mathbf{s}$ 的句子来说，至少需要 $\mathbf{s}$ 个全网络层。但这种网络结构的缺点是：

• 网络参数量是巨大，内存占用和计算代价较高，同时由于每个序列的长度 $\mathbf{s}$ 并不相同，网络结构是动态变化的；
• 每个全连接层子网络 ${\mathbf{W}}_{\mathbf{i}}$ 和 ${\mathbf{b}}_{\mathbf{i}}$ 只能感受当前词向量的输入，并不能感知之前和之后的语境信息，导致句子整体语义的缺失，每个子网络只能根据自己的输入来提取高层特征。

3.2 考虑权重共享

??针对全连接的第一个缺点，我们知道卷积神经网络之所以在处理局部相关数据时优于全连接网络，是因为它充分利用了权值共享的思想，大大减少了网络的参数量，使得网络训练起来更加高效。那在处理序列信号的问题上，我们可以借鉴权值共享的思想。

上图中，将这 $\mathbf{s}$ 个网络层参数共享，这样其实相当于使用一个全连接网络来提取所有单词的特征信息。通过权值共享后，参数量大大减少，网络训练变得更加稳定高效。但是，这种网络结构并没有考虑序列之间的先后顺序，将词向量打乱次序仍然能获得相同的输出，无法获取有效的全局语义信息。

3.3 考虑全局语义

??针对全连接的第二个缺点，我们让网络能够提供一个单独的内存变量，每次提取词向量的特征并刷新内存变量，直至最后一个输入完成，此时的内存变量即存储了所有序列的语义特征，并且由于输入序列之间的先后顺序，使得内存变量内容与序列顺序紧密关联。

上图中，将内存变量实现为一个状态张量 $\mathbf{h}$，除了原来的 ${\mathbf{W}}_{\mathbf{x}\mathbf{h}}$ 参数共享外，这里额外增加了一个 ${\mathbf{W}}_{\mathbf{h}\mathbf{h}}$ 参数，每个时间戳 $\mathbf{t}$ 上状态张量刷新为：
$${\mathbf{h}}_{\mathbf{t}}=\mathbf{\sigma }({\mathbf{W}}_{\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{W}}_{\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}?1}+\mathbf{b})$$
其中状态张量 ${\mathbf{h}}_0$ 为初始的内存状态，可以初始化为全 0，$\mathbf{\sigma }$ 为激活函数，经过 $\mathbf{s}$ 个词向量的输入后得到网络最终的状态张量 ${\mathbf{h}}_{\mathbf{s}}$，${\mathbf{h}}_{\mathbf{s}}$ 较好地代表了句子的全局语义信息，基于 ${\mathbf{h}}_{\mathbf{s}}$ 通过某个全连接层分类器即可完成情感分类任务。

3.4 循环神经网络

??经过上面的一步步分析探索，可以得到一种新型的网络结构，在每个时间戳 $\mathbf{t}$，网络层接受当前时间戳的输入 ${\mathbf{x}}_{\mathbf{t}}$ 和上一个时间戳的网络状态向量 ${\mathbf{h}}_{\mathbf{t}?1}$ ，经过：
$${\mathbf{h}}_{\mathbf{t}}={\mathbf{f}}_{\mathbf{\theta }}({\mathbf{h}}_{\mathbf{t}?1},{\mathbf{x}}_{\mathbf{t}})$$
变换后得到当前时间戳的新状态向量 ${\mathbf{h}}_{\mathbf{t}}$，并写入内存状态中，其中${\mathbf{f}}_{\mathbf{\theta }}$ 代表了网络的运算逻辑，$\mathbf{\theta }$ 为网络参数集。如果在每个时间戳上，网络层均有输出产生 ${\mathbf{o}}_{\mathbf{t}}$，${\mathbf{o}}_{\mathbf{t}}={\mathbf{g}}_{\mathbf{\gamma }}({\mathbf{h}}_{\mathbf{t}})$，即将网络的状态向量变换后输出。

上述网络结构在时间戳上折叠，可简化成：

网络循环接受序列的每个特征向量 ${\mathbf{x}}_{\mathbf{t}}$，并刷新内部状态向量 ${\mathbf{h}}_{\mathbf{t}}$，同时形成输出 ${\mathbf{o}}_{\mathbf{t}}$。对于这种网络结构，我们把它叫做 循环神经网络(Recurrent Neural Network，简称 RNN)。
??如果使用张量 ${\mathbf{W}}_{\mathbf{x}\mathbf{h}}$、${\mathbf{W}}_{\mathbf{h}\mathbf{h}}$ 和偏置 $\mathbf{b}$ 来参数化 ${\mathbf{f}}_{\mathbf{\theta }}$ 网络，并按照如下方式更新内存状态：
$${\mathbf{h}}_{\mathbf{t}}=\mathbf{\sigma }({\mathbf{W}}_{\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{W}}_{\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}?1}+\mathbf{b})$$
我们把这种网络叫做基本的循环神经网络，如无特别说明，一般说的循环神经网络即指这种实现。在循环神经网络中，激活函数更多地采用 tanh 函数。并且可以选择不使用偏执 $\mathbf{b}$ 来进一步减少参数量。状态向量 ${\mathbf{h}}_{\mathbf{t}}$ 可以直接用作输出，即 ${\mathbf{o}}_{\mathbf{t}}={\mathbf{h}}_{\mathbf{t}}$，也可以对 ${\mathbf{h}}_{\mathbf{t}}$ 做一个简单的线性变换 ${\mathbf{o}}_{\mathbf{t}}={\mathbf{W}}_{\mathbf{h}\mathbf{o}}{\mathbf{h}}_{\mathbf{t}}$ 后得到每个时间戳上的网络输出 ${\mathbf{o}}_{\mathbf{t}}$。

3.5 小结

??经过上面的推到，我们知道 RNN 是怎么来的的，内部的公式如何计算的。由上面再次总结 RNN 的核心公式如下：

• ${\mathbf{z}}_{\mathbf{t}}={\mathbf{W}}_{\mathbf{x}\mathbf{h}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{W}}_{\mathbf{h}\mathbf{h}}{\mathbf{h}}_{\mathbf{t}?1}+\mathbf{b}$；
• ${\mathbf{h}}_{\mathbf{t}}=\mathbf{\sigma }({\mathbf{z}}_{\mathbf{t}})$；
• ${\mathbf{o}}_{\mathbf{t}}={\mathbf{W}}_{\mathbf{h}\mathbf{o}}{\mathbf{h}}_{\mathbf{t}}$，若是分类问题的话，还可以是 ${\mathbf{o}}_{\mathbf{t}}=\mathbf{s}\mathbf{o}\mathbf{f}\mathbf{t}\mathbf{m}\mathbf{a}\mathbf{x}({\mathbf{h}}_{\mathbf{t}})$。

要注意的是 RNN 中的激活函数可以是 ReLU、sigmoid、tanh，不过一般来说使用 tanh 较多。

4 RNN 类型

??循环神经网络适合于处理序列数据，序列长度一般不固定，比如我们在前面举的文本分类的是有多个输入，只有一个输出；在讲解 RNN 结构时每一个输入都有一个输出，因此，RNN 应用非常广泛。我们可以根据应用场景将 RNN 分成以下几种类型：

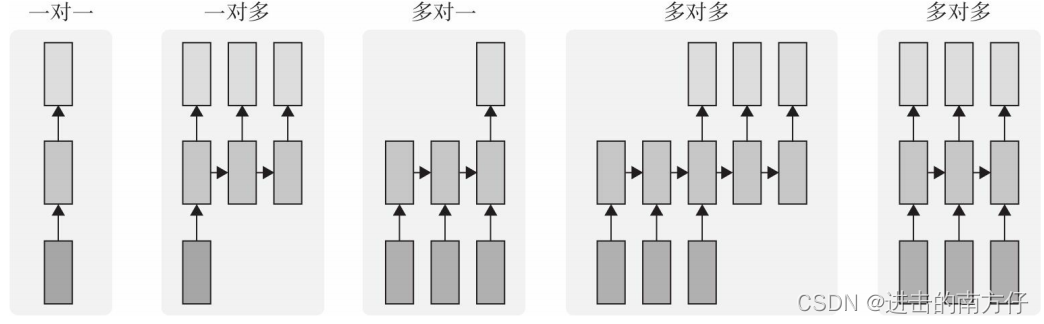
上图中每一个矩形是一个向量，箭头则表示函数(比如矩阵相乘)。 其中最下层为输入向量，最上层为输出向量，中间层表示 RNN 的状态。从左到右：

• 没有使用 RNN 的 Vanilla 模型，从固定大小的输入得到固定大小输出(比如图像分类)；
• 序列输出(比如图片字幕，输入一张图片输出一段文字序列)；
• 序列输入(比如情感分析，输入一段文字，然后将它分类成积极或者消极情感，包括雷达和我们上面举的文本分类)；
• 序列输入和序列输出(比如机器翻译：一个 RNN 读取一条英文语 句，然后将它以法语形式输出)；
• 同步序列输入输出(比如视频分类，对视频中每一帧打标签)。

此外，RNN 也可以堆叠几层，如下：

计算公式跟一层 RNN 完全一样，只是输出上有些区别，这里不展开讲述。

5 反向传播(只是探讨梯度问题)

??这篇博客就不跟大家探讨 RNN 的梯度传播了，只是探讨一下传播过程中的问题。RNN 跟别的网络结构一样，在反向传播中依然存在梯度爆炸和梯度消失的问题，主要的解决方法如下：

• 梯度爆炸：进行 梯度裁剪(Gradient Clipping)，梯度裁剪与张量限幅非常类似，也是通过将梯度张量的数值或者范数限制在某个较小的区间内，从而将远大于 1 的梯度值减少，避免出现梯度爆炸。
• 梯度消失：对网络结构进行改进，即 GRU 和 LSTM，这两种 RNN 的变种也是我下一篇要介绍的网络结构。

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖