一、 算法背景
Benders分解算法是 J.F.Benders 在1962年首先提出的,旨在解决某些大规模优化问题,其核心思想是将问题划分为多个较小的子优化问题,以取代传统优化方法中同时考虑所有决策变量和所有约束的大规模优化。由于优化问题的计算难度随变量数量和约束数量的增加而显著增加,因此迭代求解多个小规模优化问题往往比解决单个大规模优化问题更有效。本文,我们只探讨最基础的 Benders 分解算法,只考虑将混合整数规划问题分解为线性规划和整数规划两个子问题。 更深入的探讨及原理分享,后期会在本人公众号内逐一展示,欢迎关注并留言探讨~
二、原始优化问题 P 1 P_1 P1?
本文首先讨论最基础的 Benders 解耦问题形式,其优化问题形式如下:
P 1 : m i n x , ? y ? c T x + f T y s . t . ? { A x + B y = b x ≥ 0 y ∈ Y ? R q \begin{aligned} & \bm{P_1:} \mathop{min}\limits_{ x, \ y }{\ c^Tx+f^Ty} \\ & s.t.\ \begin{cases} Ax+By=b \\ x\geq 0 \\ y\in Y \subseteq \mathbb{R}^q \end{cases} \end{aligned} ?P1?:x,?ymin??cTx+fTys.t.???????Ax+By=bx≥0y∈Y?Rq??
其中, x x x 与 y y y 分别是 p 维及 q q q 维决策向量, Y Y Y是多面体, A , B A,B A,B是矩阵, b , c , f b,c,f b,c,f是对应维度的列向量,且 y y y 是整数决策变量, x x x 为连续决策变量。
三、问题解耦:主问题 P 2 P_2 P2? 与子问题 P 3 P_3 P3?
我们将上述优化问题分解为以下两个优化问题:
1)主问题 P 2 P_2 P2? 为:
P
2
:
m
i
n
y
?
f
T
y
+
q
(
y
)
s
.
t
.
??
y
∈
Y
?
R
q
\begin{aligned} & \bm{P_2:} \mathop{min}\limits_{ y }{\ f^Ty+q(y)} \\ & s.t. \ \ y\in Y \subseteq \mathbb{R}^q \end{aligned}
?P2?:ymin??fTy+q(y)s.t.??y∈Y?Rq?
其中,
q
(
y
)
q(y)
q(y) 为以下子优化问题
P
3
P_3
P3? 的值(即求解优化问题
P
3
P_3
P3? 后,得到的
c
T
x
c^Tx
cTx 的值)。
2)子问题 P 3 P_3 P3? 为:
P 3 : m i n x ? c T x s . t . ? { A x = b ? B y x ≥ 0 \begin{aligned} & \bm{P_3:} \mathop{min}\limits_{ x }{\ c^Tx } \\ & s.t.\ \begin{cases} Ax=b-By \\ x\geq 0 \end{cases} \end{aligned} ?P3?:xmin??cTxs.t.?{Ax=b?Byx≥0??
显然, P 3 P_3 P3? 在给定 y y y 时,是一个线性规划问题。由于该问题的约束条件中耦合了变量 y y y,故为便于讨论该线性优化问题,我们求其对偶形式:
四、对偶子问题 P 4 P_4 P4?
列出上述优化问题
P
3
P_3
P3? 的拉格朗日函数如下:
L
(
x
,
α
,
μ
)
=
c
T
x
+
α
T
(
b
?
B
y
?
A
x
)
+
μ
(
?
x
)
=
(
c
T
?
α
T
A
?
μ
)
x
+
α
T
(
b
?
B
y
)
\begin{aligned} L(x,\alpha,\mu) &= c^Tx + \alpha^T(b-By-Ax)+\mu(-x) \\ &=(c^T - \alpha^TA -\mu)x+\alpha^T(b-By) \end{aligned}
L(x,α,μ)?=cTx+αT(b?By?Ax)+μ(?x)=(cT?αTA?μ)x+αT(b?By)?
其中,
α
\alpha
α 与
μ
\mu
μ 为拉格朗日乘子。以
x
x
x 为决策变量极小化拉格朗日函数
L
L
L,得到以下结果:
m i n x L ( x , α , μ ) = { α T ( b ? B y ) , ?? i f ?? c T ? α T A = μ ≥ 0 ? ∞ , ?? o t h e w i s e \begin{aligned} \mathop{min}\limits_{ x }{L(x,\alpha,\mu)} = \begin{cases} \alpha^T(b-By), \ \ if \ \ c^T - \alpha^TA =\mu\geq 0 \\ -\infty, \ \ othewise \end{cases} \end{aligned} xmin?L(x,α,μ)={αT(b?By),??if??cT?αTA=μ≥0?∞,??othewise??
因此,可推出下式对偶子问题 P 4 P_4 P4?:
P 4 : m a x α ? α T ( b ? B y ) s . t . ? { A T α ≤ c α ?? u n r e s t r i c t e d \begin{aligned} & \bm{P_4:} \mathop{max}\limits_{ \alpha}{ \ \alpha^T(b-By) } \\ & s.t.\ \begin{cases} A^T \alpha \leq c \\ \alpha \ \ unrestricted \end{cases} \end{aligned} ?P4?:αmax??αT(b?By)s.t.?{ATα≤cα??unrestricted??
此时, y y y 只存在于对偶子问题的目标函数中,约束条件与 y y y 无关,换言之,约束条件形成的多面体与 y y y 无关,这么做的好处是,在迭代的过程中,无论 y 取何值,都不会对多面体的形状有任何影响。因此我们下一节才可以针对固定的多面体,讨论其 extreme point 及 extreme rays,不然多面体一直在变,会导致 extreme point 及 extreme rays 也一直在变。
五、讨论
首先,我们先回顾一下基础的对偶理论:
如下图所示,若对偶问题无解(即对偶问题中的约束条件组成的集合为空集,即:可行集为空集)。此时,原优化问题可能无解,也可能有无界解;若对偶问题存在有界解(即对偶问题中的约束条件组成的集合为非空集,且该对偶问题可求出有界解),则原优化问题也存在有界解;若对偶问题存在无界解(即对偶问题中的约束条件组成的集合为非空集,且对偶问题的解为无界解),则原优化问题无解。该基础结论可总结为下表:
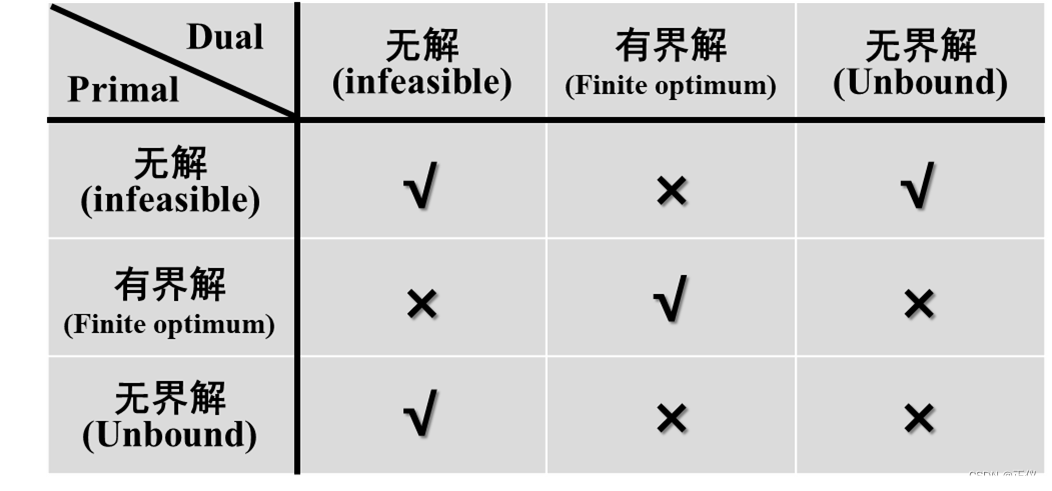
基于上述基础,我们可讨论对偶子问题 P 4 P_4 P4?:
- 若对偶子问题 P 4 P_4 P4? 无解,则子问题 P 3 P_3 P3? 无解或无界,这意味着原始优化问题 P 1 P_1 P1? 也无解或无界,无意义,不予考虑;
- 若对偶子问题 P 4 P_4 P4? 有解,则存在两种情况,要么是无界解,要么是有界解。
假设可行集(可行域)非空,即对偶子问题 P 4 P_4 P4? 有解。不妨设可行集内(即多面体内)存在 I I I 个 extreme points 及 J J J 个 extreme rays。extreme points 用 ( α p 1 , α p 2 , . . . , α p I ) (\alpha_p^1,\alpha_p^2,...,\alpha_p^I) (αp1?,αp2?,...,αpI?) 表述, extreme rays 用 ( α r 1 , α r 2 , . . . , α r J ) (\alpha_r^1,\alpha_r^2,...,\alpha_r^J) (αr1?,αr2?,...,αrJ?) 表述。其中,extreme points 与 extreme rays 的介绍见我的另一篇博客 Extreme Points and Extreme Rays。此时,对任意给定的向量 y ^ \hat{y} y^?,求解对偶子问题 P 4 P_4 P4? 后,可得到两种情况:
-
若对偶子问题 P 4 P_4 P4? 是无界解:
此时子问题 P 3 P_3 P3? 无解,且存在 extreme ray 使得 ( α r j ) T ( b ? B y ) > 0 (\alpha^j_r)^T(b-By)>0 (αrj?)T(b?By)>0。(这是因为,此时的 b ? B y b-By b?By 为常数,而该线性规划问题可行集无界,且优化问题为最大化 ( α r j ) T ( b ? B y ) (\alpha^j_r)^T(b-By) (αrj?)T(b?By),因此 ( α r j ) (\alpha^j_r) (αrj?) 可以取到正负无穷,则 ( α r j ) T ( b ? B y ) (\alpha^j_r)^T(b-By) (αrj?)T(b?By) 可取到正无穷。此时,对偶子问题 P 4 P_4 P4? 是无界解,故原子问题 P 3 P_3 P3? 无解,导致原优化 P 1 P_1 P1?也无解)。 -
若对偶子问题 P 4 P_4 P4? 是有界解:
此时,可找到一个 extreme point α p i \alpha^i_p αpi?,以最大化目标函数 ( α p i ) T ( b ? B y ) (\alpha^i_p)^T(b-By) (αpi?)T(b?By),此时,子问题 P 3 P_3 P3? 与 对偶子问题 P 4 P_4 P4? 都存在有界最优解。
六、新主问题 P 5 P_5 P5?
基于上述讨论,我们在主优化问题 P 2 P_2 P2? 中新添以下两个约束:
( α r j ) T ( b ? B y ) ≤ 0 , ? j = 1 , 2 , . . . , J ( α p i ) T ( b ? B y ) ≤ q , ? i = 1 , 2 , . . . , I \begin{aligned} &(\alpha^j_r)^T(b-By) \leq 0, \quad \forall j = 1, 2, ... , J \\ &(\alpha^i_p)^T(b-By) \leq q, \quad \forall i = 1, 2, ... , I \end{aligned} ?(αrj?)T(b?By)≤0,?j=1,2,...,J(αpi?)T(b?By)≤q,?i=1,2,...,I?
我们将第一个约束称为 Benders feasibility cuts ,我们将第二个约束称为 Benders optimality cuts 。Benders feasibility cuts 旨在排除对偶子问题中无界解的情况(即:排除 extreme ray 的情况),Benders optimality cuts 旨在提高优化问题的性能(即:寻找更好的 extreme point)。此时,主问题 P 2 P_2 P2? 可写成下式:
P
5
:
m
i
n
y
,
?
q
?
f
T
y
+
q
s
.
t
.
?
{
(
α
r
j
)
T
(
b
?
B
y
)
≤
0
,
?
j
=
1
,
2
,
.
.
.
,
J
(
α
p
i
)
T
(
b
?
B
y
)
≤
q
,
?
i
=
1
,
2
,
.
.
.
,
I
y
∈
Y
?
R
q
,
?
q
?
u
n
r
e
s
t
r
i
c
t
e
d
\begin{aligned} & \bm{P_5:} \mathop{min}\limits_{ y, \ q }{\ f^Ty+q} \\ & s.t.\ \begin{cases} (\alpha^j_r)^T(b-By) \leq 0, \quad \forall j = 1, 2, ... , J \\ (\alpha^i_p)^T(b-By) \leq q, \quad \forall i = 1, 2, ... , I \\ y\in Y \subseteq \mathbb{R}^q, \ q \ unrestricted \end{cases} \end{aligned}
?P5?:y,?qmin??fTy+qs.t.???????(αrj?)T(b?By)≤0,?j=1,2,...,J(αpi?)T(b?By)≤q,?i=1,2,...,Iy∈Y?Rq,?q?unrestricted??
我们称以上优化问题为 RMP(Relaxed Master Problem),即具有部分 cuts 的主问题。至此,基础的推导已全部完毕,下面将给出 Benders 算法的求解流程。
七、算法流程
如下图所示,算法从求解主问题 P 5 P_5 P5? 开始(需要注意的是,在首轮迭代时,不需向主问题 P 5 P_5 P5? 中添加 Benders feasibility cuts 约束及 Benders optimality cuts 约束,只需添加 q ≥ 0 q\geq 0 q≥0 的约束即可),并得到一组解 ( y ? , q ? ) (y^*, q^*) (y?,q?),并将得到的 y ? y^* y? 代入到对偶子问题 P 4 P_4 P4? 中,计算最优的 α \alpha α:
- 若得到的无界解(即:该最大化问题中得到最优解时的 α \alpha α趋于正负无穷,毕竟是纯线性规划…),则获取该对偶子问题的 extreme ray,并向主问题 P 5 P_5 P5? 中添加 Benders feasibility cuts 约束(Benders feasibility cuts 约束其实就是将 extreme ray 中的 α \alpha α 取值(并非正负无穷了哦,此为 extreme ray 中的 α \alpha α 取值,而非对偶子问题为最优解时的 α \alpha α 取值)代入到对偶子问题的目标函数中,并令代入 extreme ray 后的目标函数值小于等于0,便是 Benders feasibility cuts 约束了),并重新计算主问题 P 5 P_5 P5?,即回到流程图中“求解主问题 P 5 P_5 P5?”的那一步;
- 若得到有界解,即有界的 α ? \alpha^* α?,则计算 q ( y ? ) = ( α ? ) T ( b ? B y ? ) q(y^*)=(\alpha^*)^T(b-By^*) q(y?)=(α?)T(b?By?),比较 q ( y ? ) q(y^*) q(y?) 与 q ? q^* q?,若两者相等,则循环终止,输出最优解即可。若两者不相等,则添加 Benders optimality cuts 约束后,重新计算主问题 P 5 P_5 P5?,继续迭代循环。
收敛性:由于 extreme points 的数量 I I I 和 extreme rays 的数量 J J J 是有限的,并且在每次迭代中都会生成新的 Benders feasibility cuts 或 Benders optimality cuts,因此该方法通过有限次的迭代后必收敛,且会收敛到最优解。
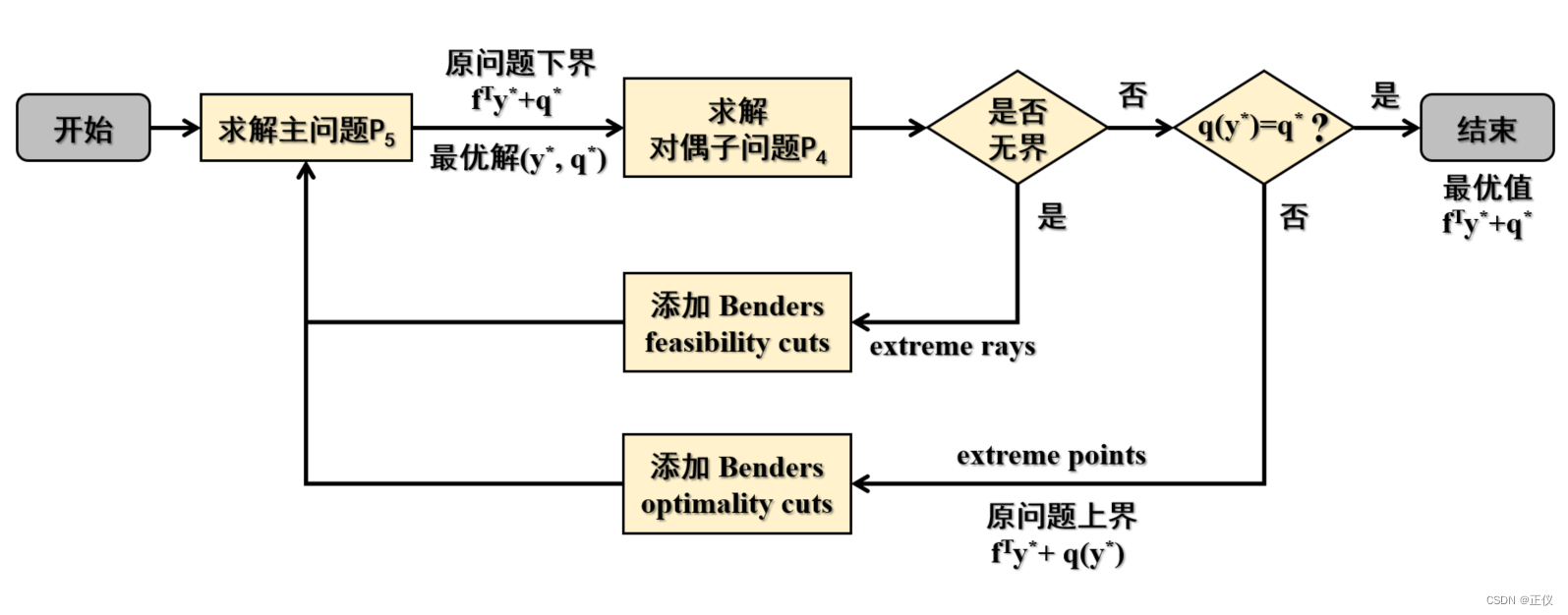
总结:Benders 解耦法实际上是将整数优化变量留在主问题中,将连续性变量解耦至子问题中,通过两层解耦法,不断迭代,求得混合整数规划问题的最优解。未来我们将更新 Benders 解耦法的 Extensions 部分。
八、参考网址
[1] 核心资料:Benders Decomposition
[2] 维基百科:Generalized Benders decomposition (GBD)
[3] Paper:Generalized Benders Decomposition
更多优化内容,欢迎关注本人微信公众号:优化与博弈的数学原理

