1感知机
1.1单层感知机
1.1.1单层感知机的模型
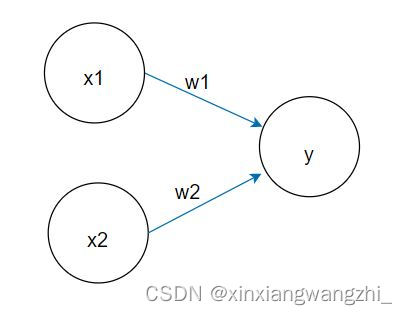
上图是一个接收两个输入信号的感知机的例子。 x 1 , x 2 x_1,x_2 x1?,x2?是两个输入信号, y y y是输出信号, w 1 , w 2 w_1,w_2 w1?,w2?是权重。图中的 ? \bigcirc ?称为神经元或者节点。输入信号被送往神经元时,会分别乘以固定的权重,神经元会计算传送过来的信号总和。只有这个总共超过某一界限 θ \theta θ,才输出1。
1.1.2单层感知机的数学解释
将上图用数学公式表示如下:
y
=
{
0
(
w
1
x
1
+
w
2
x
2
?
θ
)
1
(
w
1
x
1
+
w
2
x
2
>
θ
)
(1)
y=\left\{ \begin{aligned} 0\quad(w_1x_1+w_2x_2\leqslant \theta) \\ 1\quad(w_1x_1+w_2x_2> \theta) \end{aligned} \right.\tag{1}
y={0(w1?x1?+w2?x2??θ)1(w1?x1?+w2?x2?>θ)?(1)
令
b
=
?
θ
b=-\theta
b=?θ,则(1)式变为:
y
=
{
0
(
b
+
w
1
x
1
+
w
2
x
2
?
0
)
1
(
b
+
w
1
x
1
+
w
2
x
2
>
0
)
(2)
y=\left\{ \begin{aligned} 0\quad(b+w_1x_1+w_2x_2\leqslant 0) \\ 1\quad(b+w_1x_1+w_2x_2> 0) \end{aligned} \right.\tag{2}
y={0(b+w1?x1?+w2?x2??0)1(b+w1?x1?+w2?x2?>0)?(2)
式中:
w
1
,
w
2
,
b
w_1,w_2,b
w1?,w2?,b分别被称为权重和偏置。权重控制输入参数的重要性,偏置决定神经元被激活的容易程度。
以上就是单层感知机的模型和数学解释。
1.1.3单层感知机的作用和局限性
利用单层感知机实现电路中的与门:
与门定义:

当且仅当
x
1
,
x
2
x_1,x_2
x1?,x2?都为真(1)时,
y
=
1
y=1
y=1.对于式(2)
(
w
1
,
w
2
,
θ
)
=
(
0.5
,
0
,
5
,
?
0.7
)
(w_1,w_2,\theta)=(0.5,0,5,-0.7)
(w1?,w2?,θ)=(0.5,0,5,?0.7)可以满足与门,同样
(
w
1
,
w
2
,
θ
)
=
(
0.5
,
0
,
5
,
?
0.8
)
(w_1,w_2,\theta)=(0.5,0,5,-0.8)
(w1?,w2?,θ)=(0.5,0,5,?0.8)也可以满足与门。可以发现:设置不同的权重和偏置可以实现与门,且参数方式不唯一。
同理我们也可以通过设置权重和偏置实现与非门和或门。
局限性:
无法通过设置权重和偏置利用单层感知机实现异或门(当且仅当
x
1
x_1
x1?、
x
2
x_2
x2?中仅有一个为1时y等于1)。
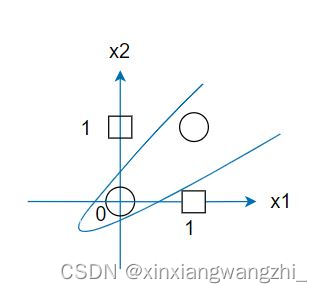
如图表示异或门,不存在一个线性可分空间表示异或门,单层感知机的局限就在于此。即:单层感知机只能表示线性空间,不能表示非线性空间。
1.2多层感知机
那么怎么实现异或门呢?答案就是多层感知机。
记NAND为与非门,AND与门,OR为或门,则异或门可以表示为:
s
1
=
N
A
N
D
(
x
1
,
x
2
)
s
2
=
O
R
(
x
1
,
x
2
)
y
=
A
N
D
(
s
1
,
s
2
)
s_1=NAND(x_1,x_2)\\ s_2=OR(x_1,x_2)\\ y=AND(s_1,s_2)
s1?=NAND(x1?,x2?)s2?=OR(x1?,x2?)y=AND(s1?,s2?)
利用单层感知机叠加成多层感知机可以实现非线性空间的异或门。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KrrDLeil-1651846819507)(./%E5%A4%9A%E5%B1%82%E6%84%9F%E7%9F%A5%E6%9C%BA.JPG)]](https://img-blog.csdnimg.cn/9c82c81001f54f7d93800f3fafc06632.png)
多层感知机示意图
通过多层感知机,可以表示更加复杂的非线性空间。从与门、或门、与非门的线性组合可以表示更复杂的非线性电路,试着推广一下,线性组合可以表示任意复杂的电路。同样的,2层感知机(可以增加变量的个数即增加输入层神经元的个数)即可在理论上近似任何函数。
