一开始的时候,我以为本节课的内容是DCT等的空间域到频率域的变换,但其实只是在空间域对图片进行两种运算。
space domain transformation:
1.algebraic transformation
2.geometric transformation
一.Space Domain Processing
由于数字图片可以看作是矩阵f(x,y),所以Space Domain Processing可以看作是以一张或多张图片为自变量(input image),一张图片为因变量(output image)的算子,即
如前面所提的,图片的空间域处理主要包括代数运算和几何运算。
代数运算的特点是多张图片(主要是同维度的)的逐像素操作,比如adding,subtraction等等;
二.Algebraic Transformation
2.1subtraction
减法最主要的作用就是用于加强图像的对比度。
减法的数学表述就是h(x,y) = f(x,y) - g(x,y)。f,g和h代表图片对应坐标像素点的量化等级。
若f(x,y)为原图,g(x,y)为背景,那么h(x,y)就是物体。

2.2??averaging
averaging的目的是为了降噪。
对噪音(这个实际上是一个随机过程)的要求是:1.均值为0,即
2.不相关,即
。
对于一副噪声图像:g(x,y)为噪声图像,f(x,y)为原图像。我们希望恢复出原图像f(x,y)。
我们对同一个场景多次拍摄(因而g(x,y)和η(x,y)均为离散随机过程;f(x,y)也是离散随机过程,只不过是i.i.d.随机过程)。假设拍设k次,则:
这是多次拍摄的噪声图片的平均;
由数学期望的运算性质易得;
从2可得只要k足够大,最终能够从噪声图片中恢复出原图片。
1.3 edge detection
edge detection利用导数得出一个导数图像,而导数图像往往代表原图的边界。。
一阶导数的定义是:对于数字图像而言,定义forward x-difference approximation为f(x+1)-f(x);定义central x-difference为f(x+1/2)-f(x-1/2)。由于f(x+1/2)=[f(x+1)+f(x)]/2,central x-difference approximation也可以定义为[f(x+1)-f(x-1)]/2。
我们知道,线性滤波器是用来逐点实现乘积求和的,所以forward x-difference approximation的线性滤波器实现为[-1,1],这样像素点得拆为[f(x),f(x+1)]的形式;central x-difference approximation的实现为[-0.5,0,0.5],这样像素点得拆为[f(x-1),f(x),f(x+1)]的形式。
然而图片是一个二维函数,所以我们应该使用方向导数。实际中我们用的最多的是梯度。其定义为:。而里面偏导数的逼近可以采取上面的一阶导数的逼近。
梯度的方向表示灰度变化最大的方向,这个方向是与边缘的切线垂直的;梯度的大小能够显示边缘的强度(灰度变化的大小)。所以对图像的每一点都计算梯度的大小,这样子边缘出的数值就会比较高,边缘内部的数值会相对低。这样子得出的gradient image就是原图的edge。
理论上计算梯度需要用到平方,但是实际上我们用下述公式逼近梯度。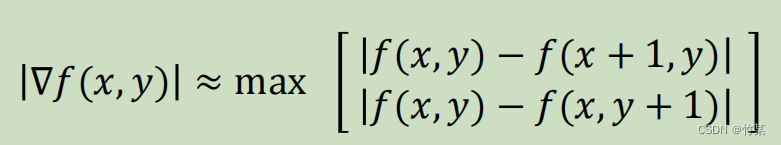
三.Geometric transformation
3.1Affine Transformation
这个可以理解为二维列向量的矩阵变换:r=Ar'。r=(x,y)表示原图中某一像素的坐标,r'=(x',y')表示变换后图中某一像素的坐标。这一变换表现在数字图像变换的特点是:
????????????????1.两点的中点保持不变;2.原来三点共线关系得到了保持。
任何线性的几何变换都是Affine Transformation的特例。如果像素的坐标表示为列向量的形式的话,任何线性的几何变化都可以表示为原坐标左乘一个2x2的变换矩阵。不过这只说明了像素坐标位置的变化,没有说明变换前后像素点量化等级的变化。
3.2 Scaling
变换矩阵为A=[a,0;0,b]。这样x'=ax, y'=by。a称为x轴上的缩放系数,b为y轴上的缩放系数。
3.3 2-D rotation
以原点为旋转中心,旋转角度为φ的几何变换的变换矩阵为A=[cosφ,-sinφ?; sinφ,cosφ]。
这样子原来(r*cosθ,r*sinθ)的坐标变为了[r*cos(θ+φ),r*sin(θ+φ)]。
3.4 翻转
关于x轴翻转x'=x,y=-y,故A=[1,0;0,-1]。
关于y轴翻转x'=-x,y'=y,故A=[-1,0;0,1]。
关于原点对称:x'=-x,y'=-y,故A=[-1,0;0,-1]
3.5 平移
平移不是线性变换,所以不能用2*2的矩阵表示。但是有一个方法可以使其用3*3矩阵表示,称为齐次坐标法。
对于二维坐标(x,y),我们构造三维坐标(x,y,1)。
这样,平移矩阵可以表示为[1,0,tx;0,1,ty;0,0,1]。
3.6 齐次坐标法
对于二维坐标(x,y),构造三维坐标(wx,wy,w)。w常取1。这样可以把一些非线性的几何变换用3*3矩阵表示。原本线性的几何变换的2*2变换矩阵也能相应地变为3*3变换矩阵。
比如围绕原点的旋转:[cosφ,-sinφ,0; sinφ,cosφ,0;0,0,1]。
3.7 复合变换
复合变换需要注意变换的顺序,毕竟矩阵乘法没有交换律。
一个复合变换的例子就是:图片围绕(x0,y0)旋转φ。这个可以视为图片:
1.在x方向平移-x0,在y方向平移-y0。矩阵A1=[1,0,-x0;0,1,-y0,0,0,1]。
2.围绕原点旋转φ。矩阵A2=[cosφ,-sinφ,0; sinφ,cosφ,0;0,0,1]。
3.在x方向平移x0,在y方向平移y0。矩阵A3=[1,0,x0;0,1,y0,0,0,1]。
所以复合运算矩阵为A3*A2*A1。
3.8 倾斜
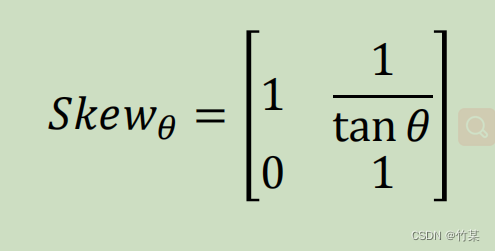
y坐标越大的点受到的x方向上的平移越大。?
