针孔照相机模型

针孔照相机模型是计算机视觉中广泛使用的照相机模型。
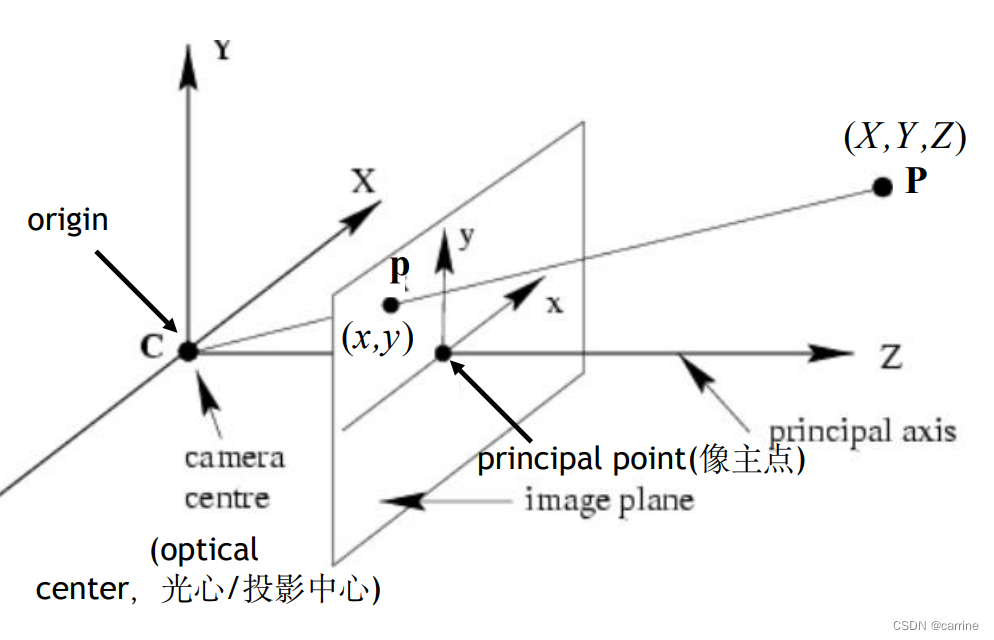
在这里插入图片描述
在针孔照相机模型中，光线投影到图像平面之前，从唯一的一个点经过，也就是照相机中心C，上图坐标系为相机坐标系，以照相机中心为原点，P代表了真实世界中的一个三维点，p代表了其映射到二维图像的点。

照相机矩阵

从坐标系的侧面看，可以看出P和p之间可以通过相似来求出他们的关系，
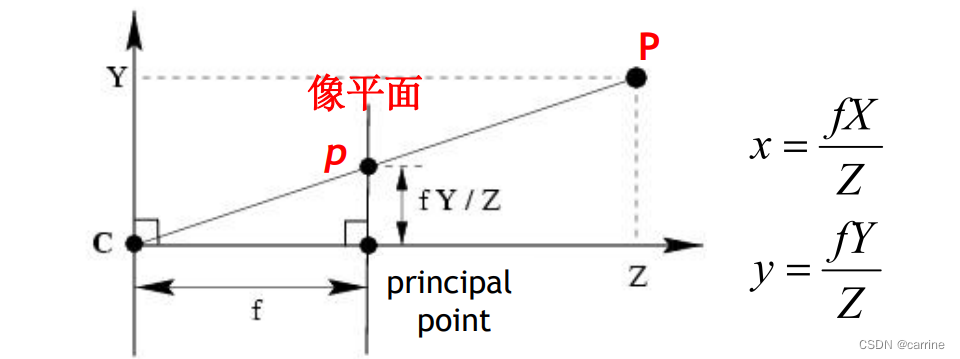
在这里插入图片描述

这里我们用矩阵来表示，
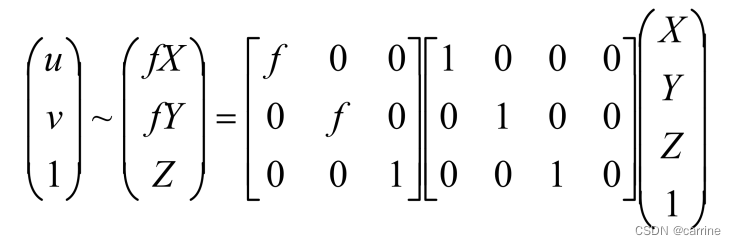
在这里插入图片描述
在相机的生产过程中，其镜头会发生偏移，也就是光心和坐标系的原点有偏移，称为主点偏移。要考虑到这个因素，所以上式要加上偏移量（u0，v0），u0代表了在x方向上的偏移量，v0代表了y方向上偏移量，变成了，

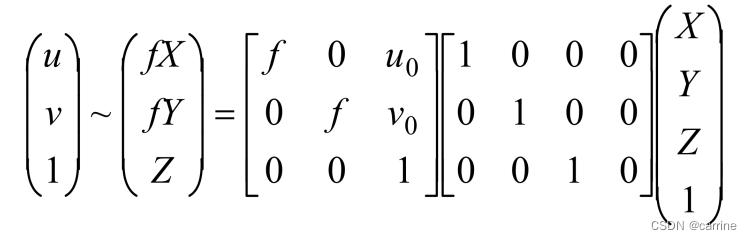
在这里插入图片描述
我们将其简写为，K代表了相机的内部参数矩阵

在这里插入图片描述
考虑到有内部参数的影响，但是还有物理层面上的影响，比如说镜头，我们日常生活中最常接触的就是广角镜头，当然了，还有许多别的镜头，只是我不知道……
不同镜头拍摄出的照片会和普通照片拍摄出来的不一样，会在某方面产生畸变，比如径向畸变、桶状畸变、枕形畸变等，为此我们还得再K中加入畸变参数，
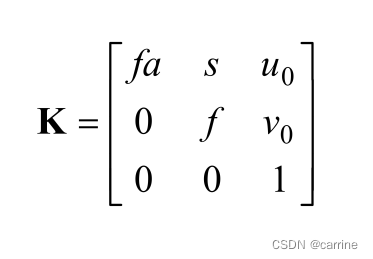
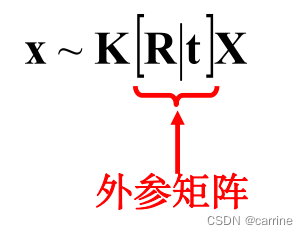
在这里插入图片描述
既然考虑好了内部参数的影响，外部环境的影响我们也要考虑，比如人为的因素，我们拿相机拍摄的时候，每次变换位置，相机位置也会跟着改变，而且有时我们会将相机旋转角度以达到更好的拍摄效果，所以还需要往照相机矩阵中加入外部参数的影响，上式变为，
在这里插入图片描述

相机参数标定

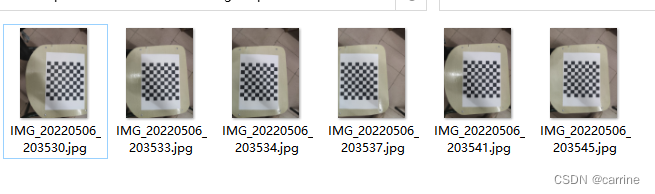
首先，我们需要进行数据采集，也就是对棋盘格进行不同角度的拍摄，在此期间，需保证棋盘格在一个平面上，否则因为纸张弯曲导致后续角点检测时出现角点间距不一致的问题。
棋盘格角点的提取。

# 寻找到棋盘角点
        succ, pic_coor = cv.findChessboardCorners(pic_data, (cross_corners[0], cross_corners[1]), None)

在这里插入图片描述

通过角点求解出单应性矩阵，再由单应性矩阵经SVD求解出内部参数。

# 求单应矩阵
    H = get_homography(pic_points, real_points_x_y)

    # 求内参
    intrinsics_param = get_intrinsics_param(H)

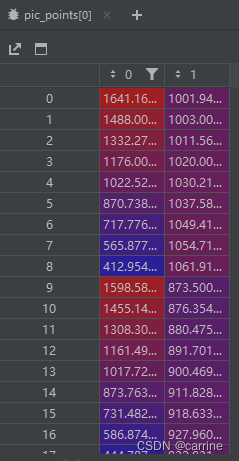
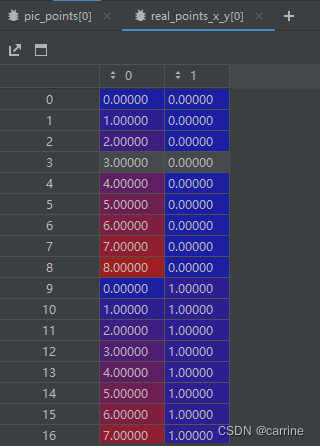
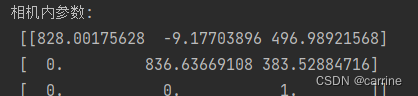
在这里插入图片描述

上述相机的内部参数是采用环形拍摄棋盘格获得的相机内参数，相机离棋盘比较近（ $1000 ? 750$ 和 $750 ? 1000$ 都有）

多种实验结果

下面采用的是平移相机对棋盘格拍照的方式获得的相机内参数，相机离棋盘比较远（ $750 ? 1000$ ）
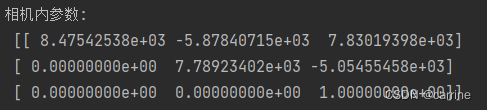
在这里插入图片描述

下面也是采用的是平移相机对棋盘格拍照的方式获得的相机内参数，相机离棋盘比较近（ $1000 ? 750$ ）

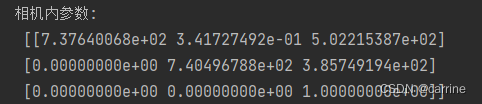
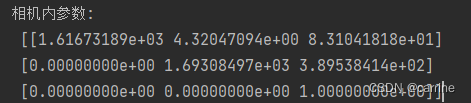
在这里插入图片描述
下面采用的是平移相机对棋盘格拍照的方式获得的相机内参数，相机离棋盘比较远（ $1000 ? 750$ ）

在这里插入图片描述

总结

通过四种不同数据得出的相机内部参数，得出几个结论：

采用相同拍摄手法的数据得出的相机内参数中的焦距相差不是很大，拍摄手法对光心的影响更大。
相机自身的旋转会造成焦距和光心与旋转前的数据相反。
平移相机拍摄的情况下，相机距离棋盘的远近得出的内参数的相差不是很大，而当相机相对于棋盘倾斜的情况下会导致内参数发生大的变化。

猜测是因为倾斜的情况下，相机中的棋盘格中，检测出的角点间距离不一致导致。这个理论也可以佐证为什么平移拍摄时内参数相差不大的情况。

主代码

import cv2 as cv
import numpy as np
import os
from step.homography import get_homography
from step.intrinsics import get_intrinsics_param
from step.extrinsics import get_extrinsics_param
from step.distortion import get_distortion



def calibrate():
    # 求单应矩阵
    H = get_homography(pic_points, real_points_x_y)

    # 求内参
    intrinsics_param = get_intrinsics_param(H)

    # 求对应每幅图外参
    extrinsics_param = get_extrinsics_param(H, intrinsics_param)

    # 畸变矫正
    k = get_distortion(intrinsics_param, extrinsics_param, pic_points, real_points_x_y)



    print("相机内参数:\t\n", intrinsics_param)
    print("畸变矫正:\t", k)
    print("外部参数:\t\n", extrinsics_param)




if __name__ == "__main__":
    i = 1;
    file_dir = r'..\pic'
    # 标定所用图像
    pic_name = os.listdir(file_dir)

    # 由于棋盘为二维平面，设定世界坐标系在棋盘上，一个单位代表一个棋盘宽度，产生世界坐标系三维坐标
    cross_corners = [9, 9] #棋盘方块交界点排列
    real_coor = np.zeros((cross_corners[0] * cross_corners[1], 3), np.float32)
    real_coor[:, :2] = np.mgrid[0:9, 0:9].T.reshape(-1, 2)

    real_points = []
    real_points_x_y = []
    pic_points = []

    for pic in pic_name:
        pic_path = os.path.join(file_dir, pic)
        pic_data = cv.imread(pic_path)

        # 寻找到棋盘角点
        succ, pic_coor = cv.findChessboardCorners(pic_data, (cross_corners[0], cross_corners[1]), None)

        if succ:
            # 添加每幅图的对应3D-2D坐标
            pic_coor = pic_coor.reshape(-1, 2)
            pic_points.append(pic_coor)

            real_points.append(real_coor)
            real_points_x_y.append(real_coor[:, :2])
            cv.drawChessboardCorners(pic_data, (cross_corners[0], cross_corners[1]), pic_coor, succ)
            cv.namedWindow('img', cv.WINDOW_NORMAL)
            cv.resizeWindow('img', 300, 300)
            cv.imshow('img', pic_data)
            cv.waitKey()
    calibrate()