[人工智能]Pytorch 语言模型和数据集

Pytorch 语言模型和数据集

0. 环境介绍

环境使用 Kaggle 里免费建立的 Notebook

教程使用李沐老师的 动手学深度学习 网站和 视频讲解

小技巧：当遇到函数看不懂的时候可以按 Shift+Tab 查看函数详解。

1. 语言模型

假设长度为的文本序列中的词元依次为 $x_1,x_2,\dots ,x_T$。 于是，$x_t$（$1\le t\le T$） 可以被认为是文本序列在时间步处的观测或标签。 在给定这样的文本序列时，语言模型（language model）的目标是估计序列的联合概率：
$$P(x_1,x_2,\dots ,x_T)$$
它的应用包括：

• 做预训练模型（如 BERT、GPT-3）
• 生成文本，给定前面几个词，不断使用 $x_t～P(x_t\mid x_{t?1},\dots ,x_1)$ 来生成后续文本
• 判断多个序列中哪个更常见，比如：“to recognize speech ” vs “to wreck a nice beach”。

1.1 若使用计数来进行建模

假设序列长度为 2，我们预测：
$$p\left(x,x^{\prime }\right)=p(x)p\left(x^{\prime }\mid x\right)=\frac{n(x)}{n}\frac{n\left(x,x^{\prime }\right)}{n(x)}$$

• 这里的 $n$ 是总词数，$n(x)$，$n(x,x^{\prime })$ 是单个单词和连续单词对的出现次数

拓展到长度为 3 的情况：
$$p\left(x,x^{\prime },x^{\prime \prime }\right)=p(x)p\left(x^{\prime }\mid x\right)p\left(x^{\prime \prime }\mid x,x^{\prime }\right)=\frac{n(x)}{n}\frac{n\left(x,x^{\prime }\right)}{n(x)}\frac{n\left(x,x^{\prime },x^{\prime \prime }\right)}{n\left(x,x^{\prime }\right)}$$

这种方式只统计词频，这完全忽略了单词的意思。“猫”（cat）和“猫科动物”（feline）可能出现在相关的上下文中， 但是想根据上下文调整这类模型其实是相当困难的。 最后，长单词序列大部分是没出现过的， 因此一个模型如果只是简单地统计先前“看到”的单词序列频率， 那么模型面对这种问题肯定是表现不佳的。

1.2 马尔科夫模型和 N 元语法

当序列很长时，因为文本量不够大，很可能 $n(x_1,\dots ,x_T)\le 1$。
使用马尔科夫假设可以缓解这个问题（拆词）：

• 一元语法（$\tau =0$，相互独立，一般不用）：
  $$\begin{array}{rl}p\left(x_1,x_2,x_3,x_4\right)& =p\left(x_1\right)p\left(x_2\right)p\left(x_3\right)p\left(x_4\right)\\ & =\frac{n\left(x_1\right)}{n}\frac{n\left(x_2\right)}{n}\frac{n\left(x_3\right)}{n}\frac{n\left(x_4\right)}{n}\end{array}$$
• 二元语法（$\tau =1$，跟前面一个值相关）：
  $$\begin{array}{rl}p\left(x_1,x_2,x_3,x_4\right)& =p\left(x_1\right)p\left(x_2\mid x_1\right)p\left(x_3\mid x_2\right)p(x_4\left|x_3\right)\\ & =\frac{n\left(x_1\right)}{n}\frac{n\left(x_1,x_2\right)}{n\left(x_1\right)}\frac{n\left(x_2,x_3\right)}{n\left(x_2\right)}\frac{n(x_3,x_4)}{n(x_3)}\end{array}$$
• 三元语法（$\tau =2$，跟前面两个值相关）：
  $$p\left(x_1,x_2,x_3,x_4\right)=p\left(x_1\right)p\left(x_2\mid x_1\right)p\left(x_3\mid x_1,x_2\right)p\left(x_4\mid x_2,x_3\right)$$

2. 代码

2.1 建立词表

时光机器数据集构建词表，并打印前 10 个频率最高的单词：

!pip install -U d2l
import random
import torch
from d2l import torch as d2l

tokens = d2l.tokenize(d2l.read_time_machine())
# 因为每个文本行不一定是一个句子或一个段落，因此我们把所有文本行拼接到一起
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus)
vocab.token_freqs[:10]

这些出现频率最高的词看起来很无聊，通常被称为停用词（stop words）。

2.2 词频图

freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)',
         xscale='log', yscale='log')

通过此图我们可以发现：词频以一种明确的方式迅速衰减。 将前几个单词作为例外消除后，剩余的所有单词大致遵循双对数坐标图上的一条直线。

2.3 二元语法

bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10]

2.4 三元语法

trigram_tokens = [triple for triple in zip(
    corpus[:-2], corpus[1:-1], corpus[2:])]
trigram_vocab = d2l.Vocab(trigram_tokens)
trigram_vocab.token_freqs[:10]

2.5 三种模型中的词元频率

bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',
         ylabel='frequency: n(x)', xscale='log', yscale='log',
         legend=['unigram', 'bigram', 'trigram'])

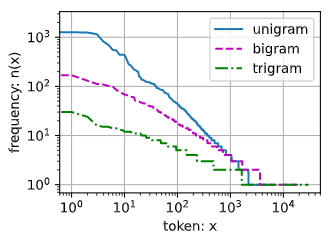
2.6 读取长序列

将长序列变成 mini-batch。

2.6.1 随机采样

在随机采样中，每个样本都是在原始的长序列上任意捕获的子序列。
在迭代过程中，来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻。 对于语言建模，目标是基于到目前为止我们看到的词元来预测下一个词元， 因此标签是移位了一个词元的原始序列：

def seq_data_iter_random(corpus, batch_size, num_steps):  #@save
    """使用随机抽样生成一个小批量子序列"""
    # 从随机偏移量开始对序列进行分区，随机范围包括num_steps-1
    corpus = corpus[random.randint(0, num_steps - 1):]
    # 减去1，是因为我们需要考虑标签
    num_subseqs = (len(corpus) - 1) // num_steps
    # 长度为num_steps的子序列的起始索引
    initial_indices = list(range(0, num_subseqs * num_steps, num_steps))
    # 在随机抽样的迭代过程中，
    # 来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻
    random.shuffle(initial_indices)

    def data(pos):
        # 返回从pos位置开始的长度为num_steps的序列
        return corpus[pos: pos + num_steps]

    num_batches = num_subseqs // batch_size
    for i in range(0, batch_size * num_batches, batch_size):
        # 在这里，initial_indices包含子序列的随机起始索引
        initial_indices_per_batch = initial_indices[i: i + batch_size]
        X = [data(j) for j in initial_indices_per_batch]
        Y = [data(j + 1) for j in initial_indices_per_batch]
        yield torch.tensor(X), torch.tensor(Y)

每次分 batch 时，丢弃前 k 个元素，从 k 位置开始往后划分。扫一遍数据，每次每个数据只用过一次。

生成一个从 $0$ 到 $34$ 的序列，假设批量大小为 $2$，时间步长为 $5$，这意味着可以生成 $?(35?1)/5?=6$ 个 “特征-标签” 子序列对， $3$ 个 batch。

my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):
    print('X: ', X, '\nY:', Y)

2.6.2 顺序分区

保证两个相邻的小批量中的子序列在原始序列上也是相邻的，这种策略在基于小批量的迭代过程中保留了拆分的子序列的顺序：

def seq_data_iter_sequential(corpus, batch_size, num_steps):  #@save
    """使用顺序分区生成一个小批量子序列"""
    # 从随机偏移量开始划分序列
    offset = random.randint(0, num_steps)
    num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
    Xs = torch.tensor(corpus[offset: offset + num_tokens])
    Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])
    Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
    num_batches = Xs.shape[1] // num_steps
    for i in range(0, num_steps * num_batches, num_steps):
        X = Xs[:, i: i + num_steps]
        Y = Ys[:, i: i + num_steps]
        yield X, Y

for X, Y in seq_data_iter_sequential(my_seq, batch_size=2, num_steps=5):
    print('X: ', X, '\nY:', Y)

2.7 封装

将上面的两个采样函数包装到一个类中， 以便稍后可以将其用作数据迭代器：

class SeqDataLoader:  #@save
    """加载序列数据的迭代器"""
    def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):
        if use_random_iter:
            self.data_iter_fn = d2l.seq_data_iter_random
        else:
            self.data_iter_fn = d2l.seq_data_iter_sequential
        self.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)
        self.batch_size, self.num_steps = batch_size, num_steps

    def __iter__(self):
        return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)

max_tokens ：当加载的数据特别大，取个小点的值训练快一点。

定义一个函数 load_data_time_machine， 它同时返回数据迭代器和词表， 因此可以与之前在 CNN 定义的 d2l.load_data_fashion_mnist 类似地使用：

def load_data_time_machine(batch_size, num_steps,  #@save
                           use_random_iter=False, max_tokens=10000):
    """返回时光机器数据集的迭代器和词表"""
    data_iter = SeqDataLoader(
        batch_size, num_steps, use_random_iter, max_tokens)
    return data_iter, data_iter.vocab

3. Q&A

Q：文本预处理中，所构建的词汇表把文本映射成数字，文本数据量越大，映射的数字就越大，这些数字还需要做预处理吗？
A：不需要，这些数字会进行 Embedding 再使用的，不会直接传入的。

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖