pyswarm库是基于python的粒子群优化库,可以采用粒子群优化的方法对优化问题进行求解。
一.简单示例
为了说明如何最好地利用pyswarm,我们将从一个完整的示例开始,随后将逐步解释:
from pyswarm import pso
def banana(x):
x1 = x[0]
x2 = x[1]
return x1**4 - 2*x2*x1**2 + x2**2 + x1**2 - 2*x1 + 5
def con(x):
x1 = x[0]
x2 = x[1]
return [-(x1 + 0.25)**2 + 0.75*x2]
lb = [-3, -1]
ub = [2, 6]
xopt, fopt = pso(banana, lb, ub, f_ieqcons=con)
# Optimum should be around x=[0.5, 0.76] with banana(x)=4.5 and con(x)=0
1.首先我们定义要最小化的目标函数,它应该定义为myfunction(x, *args, **kwargs)。换句话说,它的第一个参数是一个一维数组类对象,代表优化问题的决策变量,后面跟着任何其他(可选)参数和(同样是可选)关键字参数。函数应该返回最小化的单个标量值。在这个例子中,banana函数,就是我们的目标函数。
def banana(x):
x1 = x[0]
x2 = x[1]
return x1**4 - 2*x2*x1**2 + x2**2 + x1**2 - 2*x1 + 5
2.当优化问题中包括约束条件时,可以选择添加约束条件函数。示例中con函数即代表约束条件函数,该函数的调用语法与目标函数相同,但返回一个值数组(即使其中只有一个值)。
def con(x):
x1 = x[0]
x2 = x[1]
return [-(x1 + 0.25)**2 + 0.75*x2]
3.我们不是指定算法的起点,而是定义优化器允许搜索的输入变量的限制。lb和ub别代表下限和上限:
lb = [-3, -1]
ub = [2, 6]
4.设置好之后,我们就可以用如下的语句来调用优化器:
xopt, fopt = pso(banana, lb, ub, f_ieqcons=con)
使用f_ieqcons=con是为了告诉优化器有一个返回数组对象的约束函数。
优化完成后,pso会返回两个对象:最优决策变量值xopt和最优函数值fopt。
二.pso函数介绍
通过上述示例,我们对pyswarm库的使用有了一个简单的了解,下面我们再具体看看pso函数的完整形式:
pso(func, lb, ub, ieqcons=[], f_ieqcons=None, args=(), kwargs={},
swarmsize=100, omega=0.5, phip=0.5, phig=0.5, maxiter=100, minstep=1e-8,
minfunc=1e-8, debug=False)
在介绍时,我们参照标准粒子群算法中的速度更新公式:
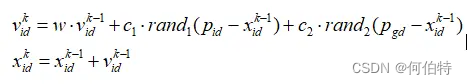
1.ieqcons
类型为list,是长度为n的函数列表,符合约束条件的决策变量x必须使ieqcons[j] (x,*args)>=0.0。
2.f_ieqcons
类型为function,该函数返回一个1-D数组,符合约束条件的决策变量必须使该数组中的每个元素都大于或等于0.0。如果指定了f_iqcons,则忽略iqcons()(默认值:None)。
3.args
类型为tuple,用于向目标函数和约束函数传递额外参数。
4.kwargs
类型为dict,用于向目标函数和约束传递额外关键字参数。
5.swarmsize
类型为int,用于设置粒子的个数,默认为100。
6.omega
类型为scalar,用于设置粒子群算法中的惯性权重,惯性权重的大小表示了对粒子当前速度继承的多少,也就是上图速度更新公式中的ω。
7.phip
类型为scalar,用于调节粒子朝p_best(当前粒子的历史最优位置)方向飞行的权重,也就是上图速度更新公式中的c1。
8.phip
类型为scalar,用于调节粒子朝g_best(粒子群的历史最优位置)方向飞行的权重,也就是上图速度更新公式中的c2。
9.maxiter
类型为int,用于设置粒子群算法的最大迭代次数,默认为100。
10.minstep
类型为scalar,用于设置粒子移动位置的最小步长,默认为1e-8。
11.minfunc
类型为scalar,用于设置目标函数的最小改变值,默认为1e-8。
12.debug
类型为bool,用于设置是否显示每一步的迭代过程,默认为false。
三.工程实例
实例中有如何添加多个自定义约束的方法。
import numpy as np
from pyswarm import pso
# Define the objective (to be minimize)
def weight(x, *args):
H, d, t = x
B, rho, E, P = args
return rho*2*np.pi*d*t*np.sqrt((B/2)**2 + H**2)
# Setup the constraint functions
def yield_stress(x, *args):
H, d, t = x
B, rho, E, P = args
return (P*np.sqrt((B/2)**2 + H**2))/(2*t*np.pi*d*H)
def buckling_stress(x, *args):
H, d, t = x
B, rho, E, P = args
return (np.pi**2*E*(d**2 + t**2))/(8*((B/2)**2 + H**2))
def deflection(x, *args):
H, d, t = x
B, rho, E, P = args
return (P*np.sqrt((B/2)**2 + H**2)**3)/(2*t*np.pi*d*H**2*E)
def constraints(x, *args):
strs = yield_stress(x, *args)
buck = buckling_stress(x, *args)
defl = deflection(x, *args)
return [100 - strs, buck - strs, 0.25 - defl]
# Define the other parameters
B = 60 # inches
rho = 0.3 # lb/in^3
E = 30000 # kpsi (1000-psi)
P = 66 # kip (1000-lbs, force)
args = (B, rho, E, P)
# Define the lower and upper bounds for H, d, t, respectively
lb = [10, 1, 0.01]
ub = [30, 3, 0.25]
xopt, fopt = pso(weight, lb, ub, f_ieqcons=constraints, args=args)
# The optimal input values are approximately
# xopt = [29, 2.4, 0.06]
# with function values approximately
# weight = 12 lbs
# yield stress = 100 kpsi (binding constraint)
# buckling stress = 150 kpsi
# deflection = 0.2 in
约束条件也可以写成如下形式:
# Setup the constraint functions
def yield_stress(x, *args):
H, d, t = x
B, rho, E, P = args
strs = (P*np.sqrt((B/2)**2 + H**2))/(2*t*np.pi*d*H)
return 100 - strs
def buckling_stress(x, *args):
H, d, t = x
B, rho, E, P = args
buck = (np.pi**2*E*(d**2 + t**2))/(8*((B/2)**2 + H**2))
strs = yield_stress(x, *args)
return buck - strs
def deflection(x, *args):
H, d, t = x
B, rho, E, P = args
defl = (P*np.sqrt((B/2)**2 + H**2)**3)/(2*t*np.pi*d*H**2*E)
return 0.25 - defl
...
cons = [yield_stress, buckling_stress, deflection]
...
xopt, fopt = pso(weight, lb, ub, ieqcons=cons, args=args)
