[人工智能]【论文阅读】Simplifying Graph Convolutional Networks

Abstract

在本文中，通过移除非线性和折叠权重矩阵来降低原来的GCN中额外的复杂性。本文从理论上分析了所得到的线性模型，并表明它对应于一个固定的低通滤波器和一个线性分类器。
实验评估表明，这些简化对许多下游应用的准确性都不会产生负面影响。此外，生成的模型可以扩展到更大的数据集，具有自然的可解释性，与FastGCN相比，可以产生高达两个数量级的加速比。

Introduction

GCNs将学习的一阶谱滤波器堆叠在一起，然后使用非线性激活函数来学习图形表示。 我们提出了SGC，通过反复消除GCN层之间的非线性，并将生成的函数折叠为单个线性变换，来降低GCN的过度复杂性。最终的线性模型在各种任务上表现出与GCN相当甚至更高的性能，同时计算效率更高，拟合的参数更少。

Simple Graph Convolution

定义$G=(V,A)$，$V$为顶点集，$A$为邻接矩阵，$D$为顶点度矩阵。每个顶点$v_i$有一个对应的$d$维的特征向量$x_i$，所有特征向量为$X$。每个顶点都属于$C$类中的一个，$Y$表示类别标签集合。
对于所有顶点集，我们知道子集标签，并希望预测未知标签。

GCN

GCN为每个节点的特征$x_i$学习一种新的特征表示，随后将其用作线性分类器的输入。在每个图卷积层中，节点表示在三个方向更新：特征传播、线性变换和逐点非线性激活 。

Feature propagation

在每个层的开始处，每个节点$v_i$的特征$h_i$用其局部邻域中的特征向量进行平均：

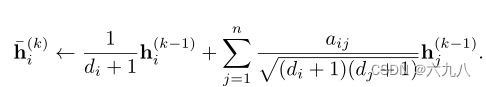
表示为矩阵运算为：
$$S={\tilde{D}}^{?1/2}\tilde{A}{\tilde{D}}^{?1/2}$$
其中$\tilde{A}=A+I$，$\tilde{D}$为对应的度矩阵。
因此所有顶点的更新为：
$${\bar{H}}^{(k)}\leftarrow S{H}^{(k?1)}$$

Feature transformation and nonlinear transition

局部平滑后，GCN层与标准MLP相同。每一层都与一个学习的权重矩阵相关联，在输出特征表示之前，逐点应用非线性激活函数，如ReLU 。
$$H^{(k)}\leftarrow ReLU({\bar{H}}^{(k)}{\Theta }^{(k)})$$
第k层的逐点非线性变换之后是第（k+1）层的特征传播。

Classifier

对于节点分类，与标准MLP类似，GCN的最后一层使用softmax分类器预测标签
$${\hat{Y}}_{GCN}=softmax(S{H}^{(k?1)}{\Theta }^{(k)})$$

Simple Graph Convolution

在GCN中，每一层中，隐藏的表示为一跳邻居之间的平均。这意味着在k层之后，一个顶点从其k层邻居中获得特征信息。
我们假设GCN层之间的非线性不是关键性的，但大部分好处来自局部平均，因此，删除了各层之间的非线性过渡函数，只保留最后的softmax，由此产生的模型是线性的，但仍然具有与K层GCN相同的增加的感受野。
$$\hat{Y}=softmax(SSS....SX{\Theta }^{(1)}...{\Theta }^{(k)})$$
令$S^k=SSS....S$，$\Theta ={\Theta }^{(1)}...{\Theta }^{(k)}$，得到下式：
$${\hat{Y}}_{SGC}=softmax(S^{K}X\Theta )$$
根据上式子可知，SGC由一个固定的（即无参数的）特征提取\平滑组件$\bar{X}=S^{K}X$，和一个线性逻辑回归分类器$\hat{Y}=softmax(\bar{X}\Theta )$组成。 由于$\bar{X}$的计算不需要权重参与，因此它基本上等同于特征预处理步骤，并且模型的整个训练减少为对预处理特征$\bar{X}$的直接多类逻辑回归。

Spectral Analysis

我们现在从图卷积的角度研究SGC。我们证明了SGC对应于图谱域上的固定滤波器。此外，我们还表明，向原始图中添加自循环，可以有效地缩小基础图谱。在这个缩放域上，SGC充当低通滤波器，在图形上生成平滑的特征。因此，附近的节点倾向于共享相似的表示，从而实现预测。

Preliminaries on Graph Convolutions

图傅立叶分析依赖于图拉普拉斯算子的谱分解。图拉普拉斯为$\Delta =D?A$（正则化形式为${\Delta }_{sym}=D^{?1/2}\Delta D^{?1/2}$），其特征分解为$\Delta =U\Lambda U^T$。拉普拉斯算子的特征分解允许我们等价地在图域上定义傅里叶变换，其中特征向量表示图的傅里叶模式，特征值表示图的频率。图的卷积操作为：
$$g?x=U\hat{G}{U}^{T}x$$
其中$\hat{G}=diag({\hat{g}}_1,...,{\hat{g}}_n)$为对角线矩阵，其中对角线对应于光谱滤波器系数。
图卷积可以用拉普拉斯算子的k阶多项式来近似 （具体见GCN），在这种情况下，滤波器系数对应于拉普拉斯特征值的多项式。最终得到：
$$g?x=\theta (I+D^{?1/2}A{D}^{?1/2})x$$
并且在GCN中，将$I+D^{?1/2}A{D}^{?1/2}$替换为${\tilde{D}}^{?1/2}\tilde{A}{\tilde{D}}^{?1/2}$

SGC and Low-Pass Filtering

初始一阶切比雪夫滤波器对应于GCN的传播矩阵:$S_{1?order}=I+D^{?1/2}A{D}^{?1/2}=2I?{\Delta }_{sym}$，因此，$S_{1?order}^K$特征传播意味着滤波器系数 ${\hat{g}}_i=\hat{g}({\lambda }_i)=(2?{\lambda }_i{)}^K$。
这里的2为单位矩阵的特征值，${\hat{g}}_i$为对$S_{1?order}^K$进行特征分解对应的特征值。

根据下图可以观察到，$S_{1?order}$的高次幂会导致滤波器系数爆炸（图中蓝线），并在${\lambda }_i<1$时过度放大信号。

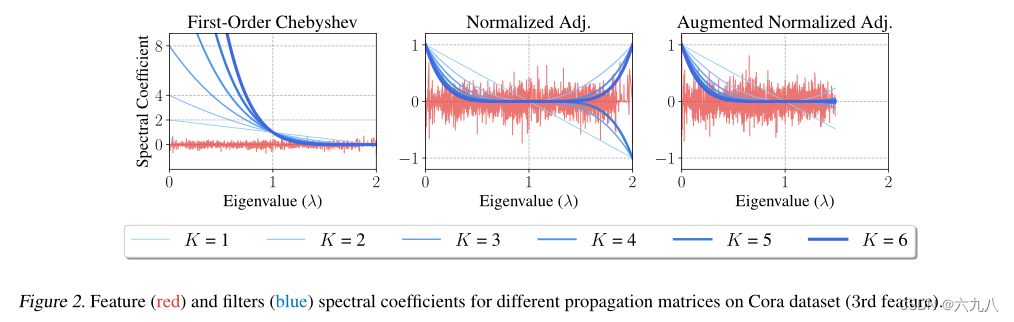
在GCN中，将$I+D^{?1/2}A{D}^{?1/2}$替换为归一化形式${\tilde{D}}^{?1/2}\tilde{A}{\tilde{D}}^{?1/2}$，本文又进一步定义增广归一化的拉普拉斯：${\tilde{\Delta }}_{sym}=I?{\tilde{D}}^{?1/2}\tilde{A}{\tilde{D}}^{?1/2}$，可以将与对应的$\tilde{S}$相关的光谱滤波器描述为潜在拉普拉斯算子特征值的多项式$\hat{g}({\tilde{\lambda }}_i)=(1?{\tilde{\lambda }}_i{)}^K$

一个小插曲：
仿照信号中的卷积，得到在图上面的卷积公式，如下经过化简以后得到了图滤波器$H=U{\Lambda }_h{U}^T$，其形式和拉普拉斯$L=U\Lambda U^T$很相似，因此，图滤波器实际上是作用在拉普拉斯矩阵特征值上的函数，它利用一个频率响应函数$h(\lambda )$来调整不同频率（即不同特征值）上分量的强度（参考：图卷积网络原来是这么回事）

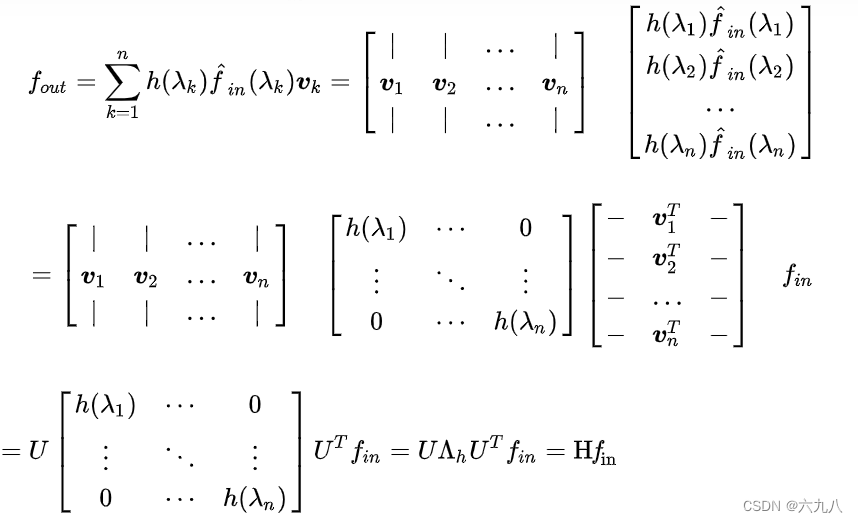
而对于增广归一化的拉普拉斯${\tilde{\Delta }}_{sym}=I?{\tilde{D}}^{?1/2}\tilde{A}{\tilde{D}}^{?1/2}=I?U\hat{\Lambda }{U}^T=U(1?\hat{\Lambda })U^T$，因此其频率响应函数为$p(\lambda )=1?{\hat{\lambda }}_i$。该函数是一个线性收缩的函数，因此能起到对图信号进行低通滤波的作用。（参考：GCN性质分析-低通滤波器）

回到原文
可以证明，向图中添加自循环会缩小相应规范化拉普拉斯算子的谱（特征值）。
定理1.归一化图拉普拉斯算子的最大特征值在加上自环后变小。

还是上图，可以看到原始的、归一化的、增广归一化的

1. 通过添加自循环，最大特征值从2缩小到大约1.5，并且消除了负系数的影响 。
2. 在第一个图中，K越大，信号会被过度放大。第二个图中，特征值的增大使得在奇数K时产生了负系数。
3. 频率响应函数在低频段上有着更强的缩放效果，该缩放频谱允许通过取$\tilde{S}$的K>1次方定义的滤波器充当低通型滤波器。

图的有效信息往往蕴含在低频段，没有必要为每一个频段训练一个参数（不用学习卷积核参数）

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖