[人工智能]Kaggle房价预测的练习(K折交叉验证)

? ? ? ? Kaggle房价预测的数据集来自house-prices-advanced-regression-techniques，如果国内用户不想翻墙的可以点击?Kaggle里的房价预测的训练数据集和测试数据集?下载即可。有了数据集之后，我们可以先打开看下具体有哪些数据，将会看到影响房价的因素有很多，比如所在位置、面积、样式、壁炉、建造年份、车库等等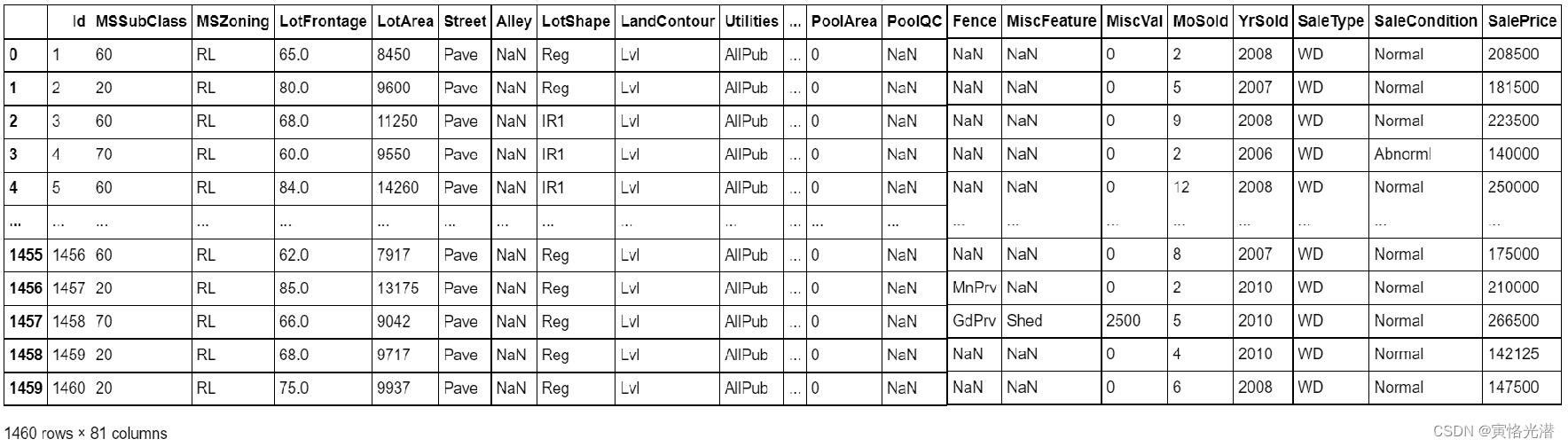

import d2lzh as d2l
from mxnet import autograd,gluon,init,nd
from mxnet.gluon import data as gdata,loss as gloss,nn
import numpy as np
import pandas as pd

train_data=pd.read_csv('data/kaggle_house_pred_train.csv')
test_data=pd.read_csv('data/kaggle_house_pred_test.csv')
train_data.shape#(1460, 81),1~1460
test_data.shape#(1459, 80),1461~2919

????????使用pandas来读取数据，查看到形状为(1460,81)，也就是说样本数有1460个，另外除了第一个ID和最后一个售价（标签值）之外，真正影响房价在本例当中是有79个因素（特征），测试集有1459个样本，其余除了没有售价（需要预测）之外，特征值是一样多的。

#查看前面5个样本数，0-6以及倒数3个的特征（最后一个是售价标签）
train_data.iloc[0:5,[0,1,2,3,4,5,6,-3,-2,-1]]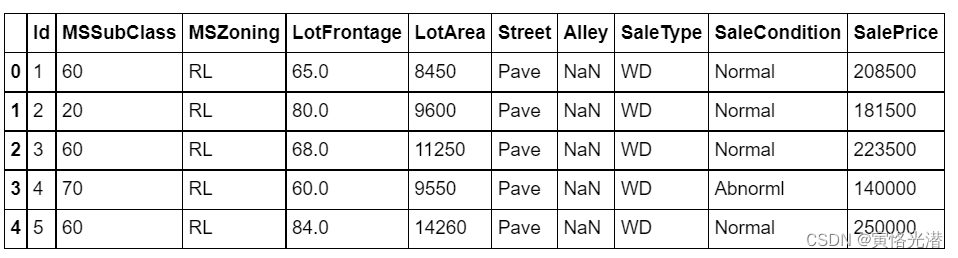

????????在训练模型之前需要先对数据集做预处理，处理一些无用的信息以及做标准化等操作，对连续值做标准化操作，让它们服从标准正态分布(特征值-均值之后除以标准差)，也就是说他们的特征值符合均值为0，标准差为1的分布，在做标准化处理之前，需要剔除类型为object的类型，我们可以先查看下这些特征值都是属于什么类型。（大家可以思考下，如果不做标准正态化处理，将出现什么样的情况？）

all_features=pd.concat((train_data.iloc[:,1:-1],test_data.iloc[:,1:]))
all_features.dtypes

MSSubClass ? ? ? ? int64
MSZoning ? ? ? ? ?object
LotFrontage ? ? ?float64
LotArea ? ? ? ? ? ?int64
Street ? ? ? ? ? ?object
? ? ? ? ? ? ? ? ? ... ??
MiscVal ? ? ? ? ? ?int64
MoSold ? ? ? ? ? ? int64
YrSold ? ? ? ? ? ? int64
SaleType ? ? ? ? ?object
SaleCondition ? ? object
Length: 79, dtype: object

可以看出有int64,object,float64，那就对object除外做标准化处理
做了标准化之后我们来看下有什么变化，数据都做了处理，这样做的好处就是数据的概率主要集中落在几个标准差之内，3个标准差之内就有99.7%的概率了，在一些要求非常严格的地方，甚至达到6个标准差(6西格玛),精度就非常非常高了

标准正态化之后的结果：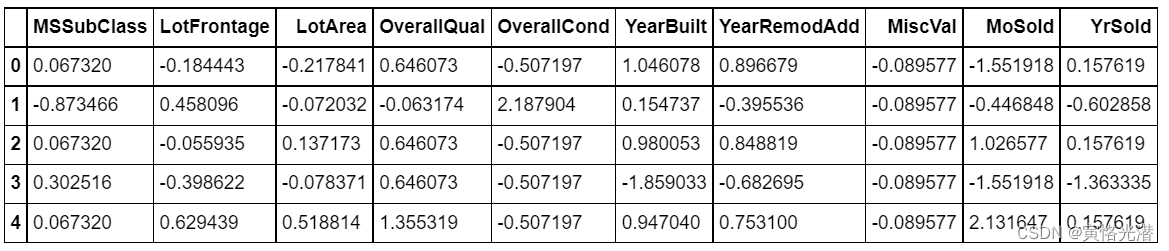

train_data=pd.read_csv('data/kaggle_house_pred_train.csv')
test_data=pd.read_csv('data/kaggle_house_pred_test.csv')
#train_data.shape#(1460, 81),1~1460
#test_data.shape#(1459, 80),1461~2919
train_data.iloc[0:5,[0,1,2,3,4,5,6,-3,-2,-1]]

#将训练集和测试集按样本连结，将得到2919个样本以及79个特征(2919, 79)
all_features=pd.concat((train_data.iloc[:,1:-1],test_data.iloc[:,1:]))

#特征的连续值做标准化(服从标准正态分布)
#print(len(all_features.dtypes[all_features.dtypes!='object'].index))#36，数值的特征
idx=all_features.dtypes[all_features.dtypes!='object'].index
all_features[idx]=all_features[idx].apply(lambda x:(x-x.mean())/(x.std()))

#缺失值NaN使用0代替（因为标准正态分布的均值是0）
all_features[idx]=all_features[idx].fillna(0)

#离散值做指示特征,将缺失值也当作合法的特征值并为其创建指示特征
all_features=pd.get_dummies(all_features,dummy_na=True)
all_features.shape#(2919, 331)从79变成331可以看出增加很多特征

#获取值并转成NDArray
n_train=train_data.shape[0]#1460
train_features=nd.array(all_features[:n_train].values)
test_features=nd.array(all_features[n_train:].values)
train_labels=nd.array(train_data.SalePrice.values).reshape((-1,1))#售价

#训练模型(平方损失函数)
loss=gloss.L2Loss()

def get_net():
    net=nn.Sequential()
    net.add(nn.Dense(1))
    net.initialize()#空参就默认随机初始化，权重参数每个元素的随机采样在-0.07到0.07之间均匀分布，偏差参数全部清零
    return net
#clip，1到无穷大，不小于1使得取对数时数值更稳定
def log_rmse(net,features,labels):
    clipped_preds=nd.clip(net(features),1,float('inf'))
    rmse=nd.sqrt(2*loss(clipped_preds.log(),labels.log()).mean())
    return rmse.asscalar()

def train(net,train_features,train_labels,test_features,test_labels,num_epochs,learning_rate,weight_decay,batch_size):
    train_ls,test_ls=[],[]
    train_iter=gdata.DataLoader(gdata.ArrayDataset(train_features,train_labels),batch_size,shuffle=True)
    trainer=gluon.Trainer(net.collect_params(),'adam',{'learning_rate':learning_rate,'wd':weight_decay})
    for epoch in range(num_epochs):
        for X,y in train_iter:
            with autograd.record():
                l=loss(net(X),y)
            l.backward()
            trainer.step(batch_size)
        train_ls.append(log_rmse(net,train_features,train_labels))
        if test_labels is not None:
            test_ls.append(log_rmse(net,test_features,test_labels))
    return train_ls,test_ls

#K折交叉验证(返回第i折交叉验证时所需要的训练和验证数据)
def get_k_fold_data(k,i,X,y):
    fold_size=X.shape[0]//k  #折成k份
    X_train,y_train=None,None
    for j in range(k):
        idx=slice(j*fold_size,(j+1)*fold_size)
        X_part,y_part=X[idx,:],y[idx]
        if j==i:
            X_valid,y_valid=X_part,y_part
        elif X_train is None:
            X_train,y_train=X_part,y_part
        else:
            X_train=nd.concat(X_train,X_part,dim=0)#指定维度参数，如果不指定，dim默认是1
            y_train=nd.concat(y_train,y_part,dim=0)
    return X_train,y_train,X_valid,y_valid

#训练K次，并返回训练和验证的平均误差
def k_fold(k,X_train,y_train,num_epochs,learning_rate,weight_decay,batch_size):
    train_ls_sum,valid_ls_sum=0,0
    for i in range(k):
        data=get_k_fold_data(k,i,X_train,y_train)
        net=get_net()
        train_ls,valid_ls=train(net,*data,num_epochs,learning_rate,weight_decay,batch_size)
        train_ls_sum+=train_ls[-1]
        valid_ls_sum+=valid_ls[-1]
        if i==0:
            d2l.semilogy(range(1,num_epochs+1),train_ls,'epochs','rmse',range(1,num_epochs+1),valid_ls,['train','valid'])
        print('fold %d,train rmse %f,valid rmse %f'%(i,train_ls[-1],valid_ls[-1]))
    return train_ls_sum/k,valid_ls_sum/k

k,num_epochs,lr,wd,batch_size=5,100,8,0,64
train_ls,valid_ls=k_fold(k,train_features,train_labels,num_epochs,lr,wd,batch_size)
print('%d-fold validation:avg train rmse %f,avg valid rmse %f'%(k,train_ls,valid_ls))

?????????其中评价模型使用的是对数均方根误差（LRMSE,Log Root Mean Squared Error）,其数学公式为：?????

????????其中K折交叉验证，可以把训练数据集拆分成K份，其中可以指定第几份作为验证数据集，其余的连结起来作为训练数据集，这样的好处就是充分利用数据集，作用是用来选择模型设计并调节超参数。

最后我们来预测测试数据集里的房屋的售价

#预测并保存结果（也可以提交到Kaggle）
def train_and_pred(train_features,test_features,train_labels,test_data,num_epochs,lr,wd,batch_size):
    net=get_net()
    train_ls,_=train(net,train_features,train_labels,None,None,num_epochs,lr,wd,batch_size)
    d2l.semilogy(range(1,num_epochs+1),train_ls,'epochs','rmse')
    print('train rmse %f'%train_ls[-1])
    preds=net(test_features).asnumpy()
    test_data['SalePrice']=pd.Series(preds.reshape(1,-1)[0])
    result=pd.concat([test_data['Id'],test_data['SalePrice']],axis=1)
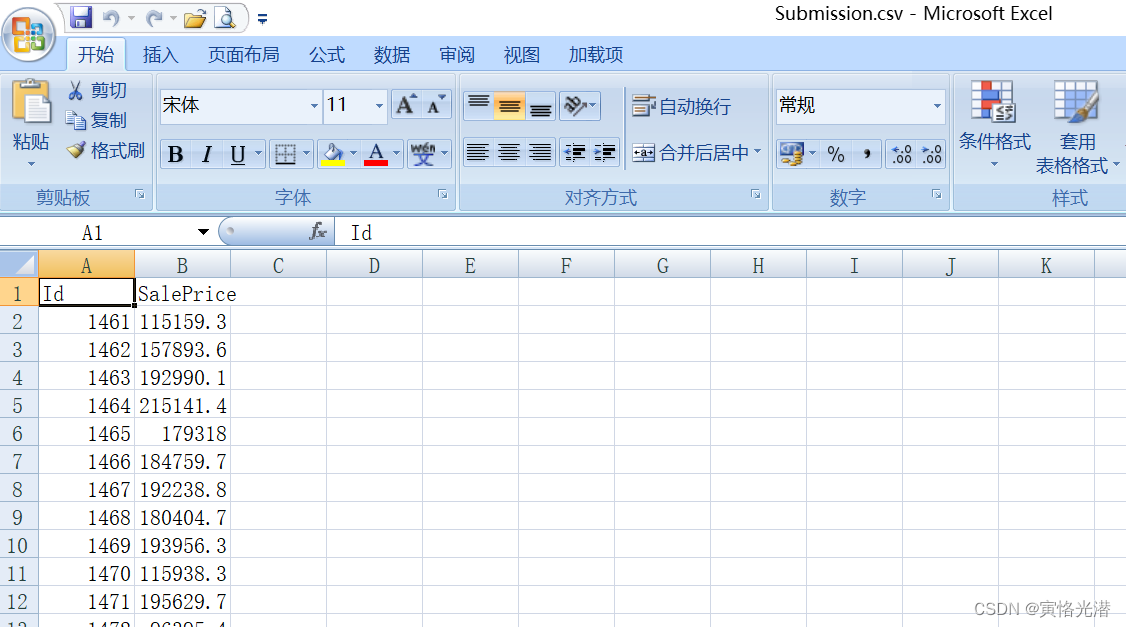
    result.to_csv('Submission.csv',index=False)

train_and_pred(train_features,test_features,train_labels,test_data,num_epochs,lr,wd,batch_size)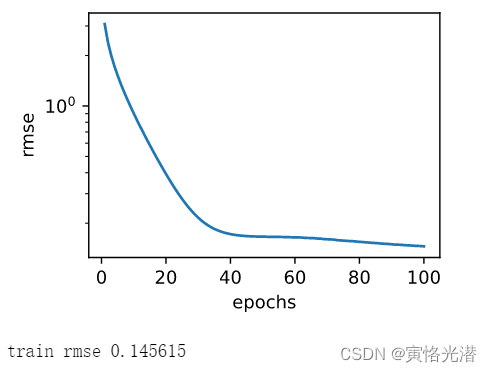

?

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖