Lecture04 real-time shadow 2
1 PCF的数学原理:Filter / Convolution
\qquad 在shadow map上应用PCF算法做深度测试的时候,不是与单个纹素作比较,而是周围一圈 n × n n\times n n×n个记录的深度是否遮挡住了该着色点,最后进行加权平均得到一个(0,1)的值,作为该着色点可见性(阴影软硬程度)的描述。
这个算法的过程,在数学上称为卷积
可以用这个简化的公式表示: [ w ? f ] ( p ) = ∑ q ∈ N ( p ) w ( p , q ) f ( q ) \displaystyle[w * f](p)=\sum_{q∈N(p)}w(p,q)f(q) [w?f](p)=q∈N(p)∑?w(p,q)f(q)
| 符号 | 意义 |
|---|---|
| f ( p ) f(p) f(p) | 返回着色点p实际深度与shadow map上的深度的比较结果,非0即1 |
| [ w ? f ] [w * f] [w?f] | ? * ?为卷积符号,表示对函数 f f f应用一个卷积 |
| [ w ? f ] ( p ) [w*f](p) [w?f](p) | 被卷积后的函数 f f f在传入着色点 p p p后应该返回什么值 |
| q ∈ N ( p ) q∈N(p) q∈N(p) | p点附近的一个点q |
| w ( p , q ) w(p,q) w(p,q) | q点对应的权值,可以根据q到p的距离得到 |
| ∑ q ∈ N ( p ) w ( p , q ) f ( q ) \displaystyle\sum_{q∈N(p)}w(p,q)f(q) q∈N(p)∑?w(p,q)f(q) | shadow map上,把p邻域的一个点q深度与p实际深度作比较(非0即1),再乘以对应的权值,然后对每个q的加权后的结果进行相加,得到 [ 0 , 1 ] [0,1] [0,1]内一个数作为着色点的visibility返回 |
PCSS更详细的公式是这个:
V ( x ) = ∑ q ∈ N ( p ) w ( p , q ) ? χ + [ D S M ( q ) ? D s c e n e ( p ) ] \large \displaystyle V(x)=\sum_{q∈N(p)}w(p,q)·\chi^+[D_{SM}(q) -D_{scene}(p)] V(x)=q∈N(p)∑?w(p,q)?χ+[DSM?(q)?Dscene?(p)]
| 符号 | 意义 |
|---|---|
| V ( x ) V(x) V(x) | Visibility 可见性;可见:1,不可见:0 |
| χ + \chi^+ χ+ | 符号函数,LaTex符号:\chi,读音“铠”,很多人也读作"卡",卡方分布 χ 2 \chi ^2 χ2也是这个符号。自变量大于0返回1,小于0返回0 |
| D S M D_{SM} DSM? | q点在shadow map中记录的深度 |
| D s c e n e ( p ) D_{scene}(p) Dscene?(p) | 场景中着色点p的实际深度 |
| w ( p , q ) w(p,q) w(p,q) | q对应的权值 |
有了严谨的数学表达式,我们可以严谨的定义一下错误的理解PCSS所对应的数学表达式是什么样的
- PCF
不是filtering shadow map,即对周围深度做平均,然后用平均深度跟着色点p深度进行比较,这样结果必然非0即1
V ( x ) ≠ χ + { [ w ? D S M ] ( q ) ? D s c e n e ( p ) } \displaystyle V(x)\ne\chi^+\{[w*D_{SM}](q) -D_{scene}(p)\} V(x)?=χ+{[w?DSM?](q)?Dscene?(p)} - PFC
也不是在最终生成有锯齿的硬阴影的图像上,做filtering
V ( x ) ≠ ∑ y ∈ N ( x ) w ( y , x ) V ( x ) \displaystyle V(x)\ne\sum_{y∈N(x)}w(y,x)V(x) V(x)?=y∈N(x)∑?w(y,x)V(x),x对应图像中的某个点,y是x附近某个点,V是图像
2 PCSS回顾
- Step1:Blocker Search
? ? \quad\ \: ?对于每个着色点p,找到shadow map上一块区域,计算遮挡物的平均深度,把区域所有texel都找一遍,判断是不是遮挡物,如果是遮挡物,则累加,最后除以遮挡物的个数。 - Step2:Penumbra Estimation
?? ? \quad\ \ \: ??公式算出W半影,根据这个得到filter size - Step3:Percentage Closer Filtering
这些步骤里,哪些特别慢?
第1、3步,每个着色点都要遍历深度图上一大片区域的纹素,并且这两步里面都要这样遍历,就很费性能- 想要阴影够软,需要大的filter size,大filter size 导致计算缓慢。
工业界较多的做法是在该区域里随机采样(稀疏采样),而不遍历区域中每一个像素,这样虽然快,但是结果会比较多噪点。如果要修复这些噪点,还可以用一些图像空间的方法来降噪。这一块技术在实时光追的课程中会说到
另一种比较好的解决方式,是VSSM
3 Variance Soft Shadow Mapping(VSSM)
\qquad 这个算法是对PCSS算法的改进,可以更快得出近似的结果
3.1 VSSM对PCF的优化
PCSS中的 Percentage Closer Filtering目的是什么?
- 找到着色点对应到shadow map上周围某区域中,比该着色点深度更浅的点的比例是多少
- 也就是,在搜索区域内有多少比shading point深度更浅的像素
- 类比于找到这场考试里比我成绩更好的学生们,看我的排名占百分之几
我想知道我的排名,但我又不香看每个学生的成绩,咋办?
- PCF原本的做法,遍历每个学生,相当于生成一个直方图如下,成绩比我好的占比多少一目了然
- 不那么准确但特别近似的方法:得到一个正态分布曲线(normal distribution)
定义正态分布需要两个条件:均值(期望)、方差
均值决定了波峰在哪,方差决定区间范围

VSSM的第一个核心思想Key idea: 快速计算得到一个区域的深度均值(mean)和方差(variance)
(1) 求均值(Mean/Average)
- MIPMAP(不准,且对长方形不友好)
- Summed Area Tables(SAT)
(2) 求方差(Variance)
- V a r ( X ) = E ( X 2 ) ? E 2 ( X ) Var(X)=E(X^2)-E^2(X) Var(X)=E(X2)?E2(X) —— 借助数学公式,通过两种期望值,就能求得方差
| V a r ( X ) Var(X) Var(X) | X区域的方差 |
|---|---|
| E ( X 2 ) E(X^2) E(X2) | X区域所有深度的平方的期望(这就需要生成一张记录深度的平方shadow map) |
| E 2 ( X ) E^2(X) E2(X) | X区域的所有深度值的期望的平方(用原本的shadow map即可算出) |
所以求方差需要额外生成一张深度的平方的shadow map
(3) 根据均值和方差,得到呈正态分布的PDF —— 实际上不需要这一步(有切比雪夫不等式可跳过此步骤)
- 欲得到shadow map 上某块区域上比着色点更近的纹素的百分比
- 计算概率密度函数PDF(Probability Density Function)阴影部分面积。
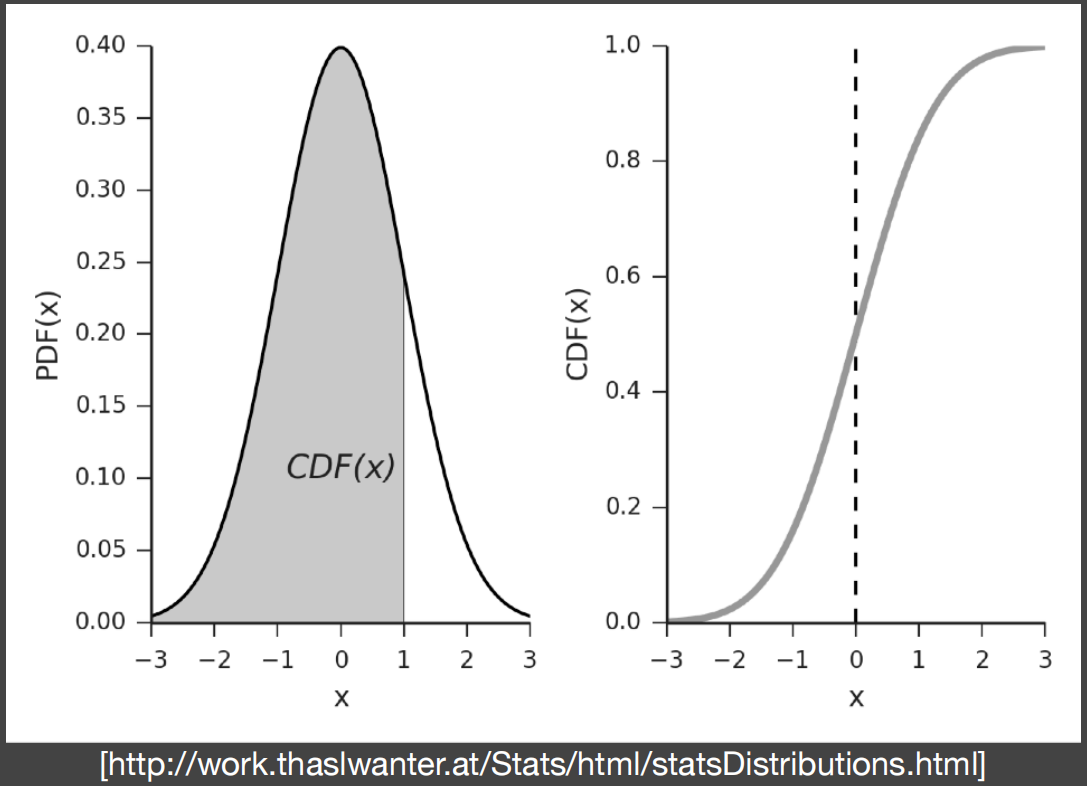
PDF:用某一区间上的积分来刻画随机变量X落在这个区间中的概率
CDF:CDF求导就是PDF,PDF对某区域求积分 == CDF对某块区域做减法,即 ∫ ? 3 ? 1 P D F ( x ) d x = C D F ( 1 ) ? C D F ( ? 3 ) ∫_{-3}^{-1}PDF(x)dx=CDF(1)-CDF(-3) ∫?3?1?PDF(x)dx=CDF(1)?CDF(?3)
要得到上面的概率密度函数(分布),还是挺麻烦的,而且相对来说还是"过于精确",从而下面VSSM算法又找到一个经典不等式
3.1.1 切比雪夫不等式(Chebychev’s inequality)
P
(
x
>
t
)
≤
σ
σ
2
+
(
t
?
μ
)
2
\displaystyle\Large\mathbf\color{red}{P(x>t)≤\frac{σ}{σ^2+(t-\mu)^2}}
P(x>t)≤σ2+(t?μ)2σ?
μ
:
m
e
a
n
?
σ
2
:
v
a
r
i
a
n
c
e
\mu: mean\:\qquad\sigma^2:variance
μ:meanσ2:variance
- 通过这个不等式,可以得到:随机变量取值超过 t t t 的概率,也可理解成得到超过t的数量占比多少
- 不需要知道该随机变量分布长什么样(实际上正不正态都不太重要),只需要知道该分布的期望和方差
- 也就是上面第(3)步没用了
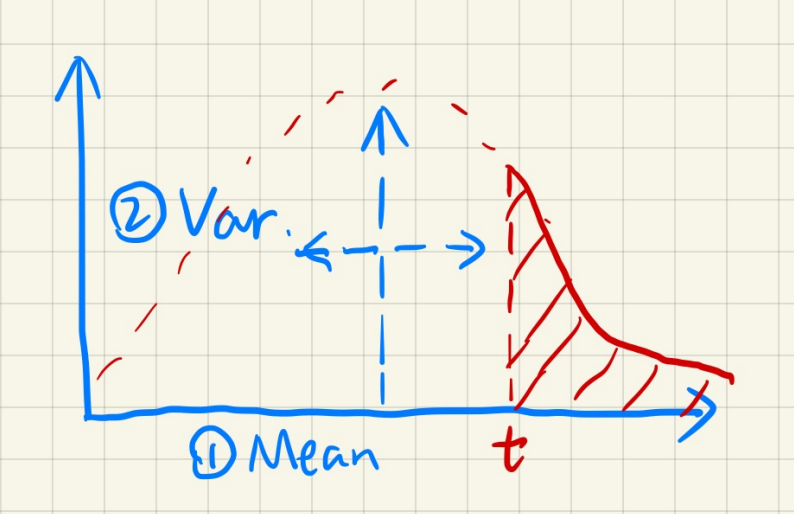
这个不等式用在PCF上,直接可以得知深度超过t的texel的百分比P,P直接就是该点的Visbility值
这个"约等式",有个条件,就是t必须在均值的右边,否则值是不准的,但是在实时渲染里效果依然很好
2.1.2 VSSM加速PCF的步骤总结
- 生成shadow map的同时,生成一张存放深度的平方的平方深度图(Square depth map)
- 求深度图上某区域的
均值,MipMap,不用循环,O(1) - 求平方深度图上某区域的
均值,依旧MipMap,O(1) - 知道两个均值,根据公式
V
a
r
(
X
)
=
E
(
X
2
)
?
E
2
(
X
)
\small Var(X)=E(X^2)-E^2(X)
Var(X)=E(X2)?E2(X)得到
方差 - 根据切比雪夫不等式,直接求出该点可见性
Visibility
现在来看,是否完美解决了第三步PCF特别慢的问题?—— 是
- 生成多张MipMap、一张平方深度图,开销很小,因为GPU对于一张图生成MipMap速度特别快,可以认为几乎不花时间,另一个没有介绍的(SAT)的生成相对慢一点
- 不需要
循环遍历区域所有像素,然后一个个的比较,最后加权求和,很大程度的减少了计算量
PCSS第一步:Blocker search特别慢的问题还没解决
Blocker search
- 求平均的遮挡物的深度,把区域所有texel都找一遍,判断是不是遮挡物,如果是遮挡物,则累加,最后除以遮挡物的个数,如着色点深度为7,则应该计算shadow map上蓝色区域的深度作为平均遮挡物深度
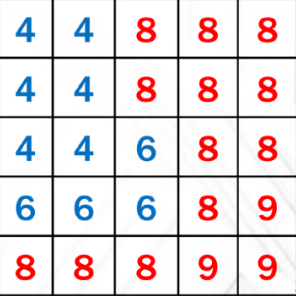
- 这一步实际上不是区域上所有纹素的平均,而是那些z<t的纹素记录的深度求平均,很慢
3.2 VSSM对Blocker Search的优化
目标:得到遮挡物的平均深度
Z
o
c
c
Z_{occ}
Zocc?
Key idea:搞些小手段,弄到非遮挡物的平均深度
Z
u
n
o
c
c
Z_{unocc}
Zunocc?
首先两者一定满足这个等式
N
1
N
Z
u
n
o
c
c
+
N
2
N
Z
o
c
c
=
Z
A
v
g
\displaystyle \frac{N_1}{N}Z_{unocc}+\frac{N_2}{N}Z_{occ} = Z_{Avg}
NN1??Zunocc?+NN2??Zocc?=ZAvg?
N
1
N_1
N1?:非遮挡物纹素个数,
N
2
N_2
N2?:遮挡物纹素个数,
N
N
N:总的区域纹素个数,
Z
A
v
g
Z_{Avg}
ZAvg?:总的区域深度均值
- 这两个权重刚好又能用
切比雪夫近似: N 1 N = P ( x > t ) ? , N 2 N = 1 ? P ( x > t ) \displaystyle\color{blue} \frac{N_1}{N} = P(x > t)\ ,\frac{N_2}{N} = 1-P(x > t) NN1??=P(x>t)?,NN2??=1?P(x>t) - 通过MipMap范围查询可得 Z A v g \color{blue}Z_{Avg} ZAvg?,我们想要得到 Z o c c Z_{occ} Zocc?,还有个未知量 Z u n o c c Z_{unocc} Zunocc?没算出来,
- 近似: Z u n o c c = t \color{blue}Z_{unocc} = t Zunocc?=t
- 唯一的未知量 Z o c c \color{red}Z_{occ} Zocc?自然就能求出
Z u n o c c = t Z_{unocc} = t Zunocc?=t,这个近似看起来就很疯狂了,但是也还是有道理,就认为所有不能遮挡着色点的场景点都分布在跟着色点同一个平面,这样肯定会在某些场景出现问题,但基本上可以忽略。总而言之大胆假设,渲染图看起来是对的,他就是对的!相比于那一丁点误差,极大的节省了计算量,是非常划算的。
VSSM能够做到这个效果
VSSM效果非常好,但是工业界依然更倾向于随机采样,得到有噪点的阴影结果,因为稀疏采样相对VSSM来说还是更快,噪声可以在成图之后,运用图像处理的一些技术去降噪

VSSM可以理解为PCSS的加速版本,虽然现在大多数还是用PCSS+区域随机采样做软阴影,但是VSSM依然值得学习,因为它所用到的近似的思想是非常值得学习的,妙蛙。
3.3 范围查询MIPMAP和SAT
- VSSM的关键是
切比雪夫近似,切比雪夫近似的关键是均值 - 因此VSSM算法最关键的点:
快速获得某区域均值 - 范围查询的这两种方法,都是一种
预计算。MIPMAP速度快,SAT百分百准确
3.3.1 MIPMAP
- 特点:
快速、近似、正方形

- 因为是插值,所以不准确。当查询区域在某层上不太对齐像素格的时候,需要
双线性插值。 - 同时当查询范围为方形但不是
2
n
2^n
2n 时,还要再进行一次层间插值,即
三线性插值 - 如果查询区域是长方形区域查询,还得加入
各向异性过滤 - MIPMAP怎么搞都是有误差的,相比之下如果查询范围小的话,误差可以接受
3.3.2 SAT(Summed Area Table)
- 它可以得到
百分百准确范围查询结果,但是计算花销肯定比MIPMAP要多 - 它是与
前缀和(prefix sum)算法息息相关的数据结构 - 均值 = 总和 / 个数,因此
范围求均值等价于范围求和
(1)一维前缀和算法
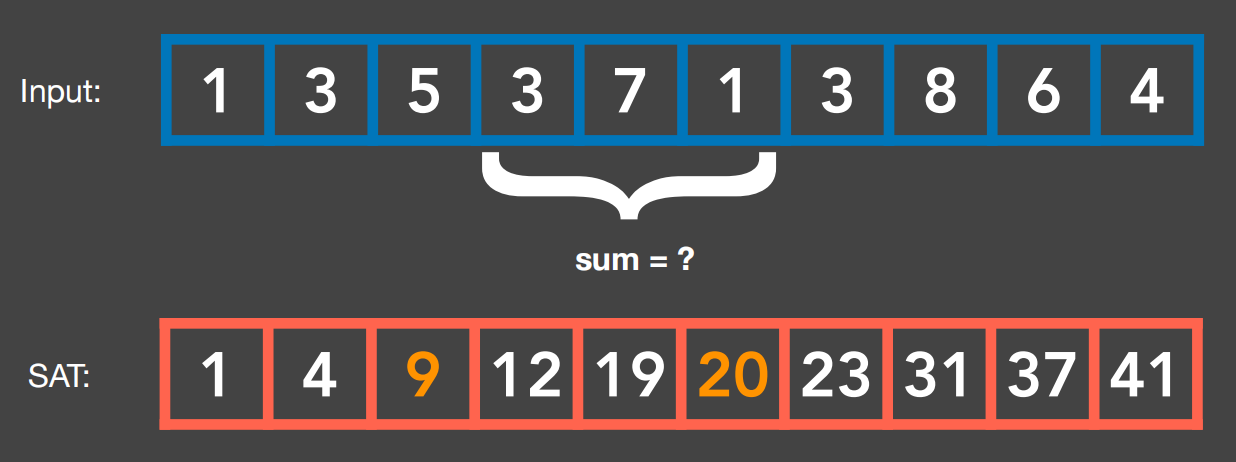
-
SAT这种数据结构实际上就是对输入的数组做一个
预处理。 -
先花费
O(n)的时间从左到右走一遍,同时做累加操作,并存入数组SAT中。 -
最后SAT上任意的一个元素就等于原来数组从最左边的元素到这个元素的和。
-
此时我们要求某区域(比如上面数组第4个到第6个元素的和),直接用SAT数组的
第6个元素-第3个元素
(2)二维前缀和算法
一个轴对齐的矩形,蓝色矩形内元素总和 = 左上角大绿色矩形 - 左边一个长条矩形 - 上边长条矩形 + 左上角小矩形

- 等式右边的四个矩形,共同的特点:
都从左上角出发 - 同一维的情况,这里也可做一个SAT表,每个元素存放的是左上角到当前元素的和
- 求任何区域的和,只需要查表4次(图中白点)就可以得出精准的区域和。
图中的两个坐标轴可以不用看,把左上角当做数组起点。也可以就把数组起点放在左下角,重新推一遍上述的计算过程。
二维SAT建立步骤(妙)
- 对数组
每一行建立SAT,数组的每个元素存放的是当前行从左边第一个元素到当前点的和 - 在第一步生成的SAT二维数组的基础上,再对数组的每一列做累加,
生成另一个SAT - 此时的SAT每个元素,存放的才是数组起点到当前点的一个矩形区域内的元素总和
- 乍一看复杂度为 O ( n 2 ) O(n^2) O(n2),但是如果算法写得好,充分利用GPU的并行计算,还是挺快的
GPU对于算法的复杂度,不能直接断定 O ( n 2 ) O(n^2) O(n2)的算法一定比 O ( n ) O(n) O(n)更好,还要考虑并行度
4 Moment Shadow Mapping
这是非常前沿的算法,因为图像空间的降噪的盛行,PCSS重新上位,这个算法也渐渐没人用了实现起来也相对比较麻烦。
4.1 VSSM算法的局限性
VSSM做了很多假设,因此结果相当近似且有局限性
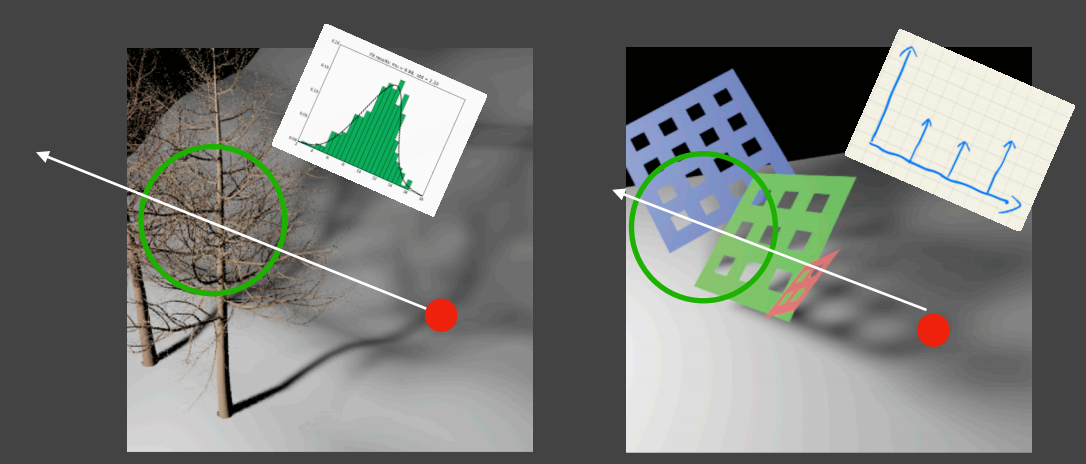
- 上图所示,VSSM算法在类似树枝这种特别多且复杂的场景时,假设是正态分布确实可以得到比较好的近似结果
- 如果是右边这种场景就不行,着色点连向光源在shadow map上周围的像素记录的深度分布,就应该接近三个遮挡物深度,形成三个峰值。那么深度分布采用正态分布就特别不准确
现在考虑如下蓝色深度分布错用红色正态分布进行VSSM计算

- 不是正态分布强行按正态分布算就会出现
漏光or过暗的结果,因为切比雪夫计算结果不准确,偏大或偏小阴影某些地方过暗可以接受,但是漏光、偏白就接受不了 - 比如上图这种情况,错误的用红色曲线代替蓝色,本来蓝色部分,深度大于t的假设为30%,结果红色计算结果是50%,阴影就变白了
漏光(Light leaking)
- 很明显这辆车子的深度并不是正态分布,因为车是镂空的,从漏光处连向光源,在shadow map上的周围一圈的深度基本击中在车的底板构件的深度值附近以及车顶的框架深度。强行用正态分布来计算,就会出现漏光
- 但是过暗基本看不出来,可以忽略

4.2 Moment Shadow Mapping
为了解决VSSM的其中一个问题:深度分布描述不准确
提出这种方法:引入更高阶的moments(矩)来得到更加准确的深度分布情况
Moments
- 定义五花八门
- 最简单的一种:就是记录一个数的1,2,3,4…n次方, x , x 2 , x 3 , . . . x,x^2,x^3,... x,x2,x3,...记录多少次方就表示保留多少矩
- VSSM记录了深度图的1、2次方,就等于用了
前两阶的矩 - 这样多记录几阶矩就能得到更准确的结果
- 保留前m阶的矩,就能生成台阶数为m/2的阶跃函数,可以看做类似于泰勒展开式一样,项数越多,拟合得就越好,
一般来说4阶就够用。 - 下图可以看到,绿色曲线就是4阶矩对应的阶跃函数,可以很好的拟合PCF曲线,如果是3阶、2阶效果就很差,2阶就是VSSM用的正态分布PDF对应的PCF的曲线
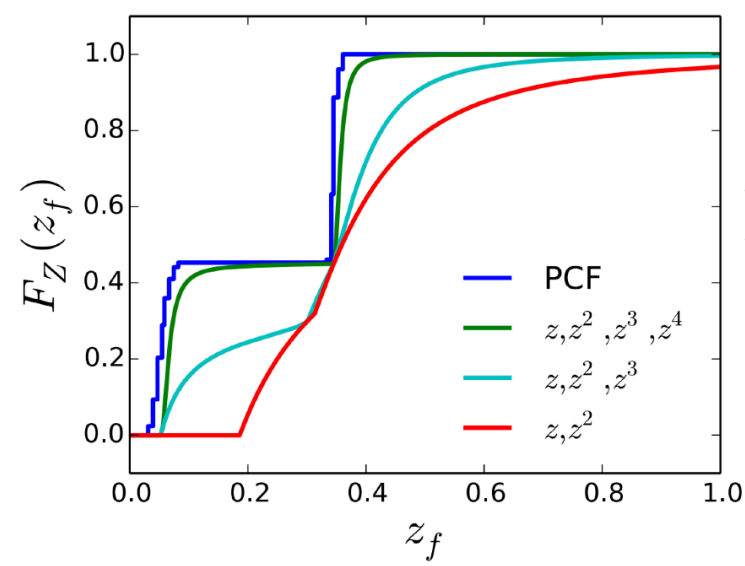
Moment shadow mapping VS Variance soft shadow mapping
优势:非常好的结果、修复漏光现象
劣势:多一些存储空间,多一些计算量

最后,怎么通过前4阶矩得到 2个台阶的阶跃函数,请参考Peters的论文
