华中杯 A题简单复盘(附Python 源码)
文章目录
前言
五一和队友们一起坐牢了打完了华中杯,只能说确实有点小折磨。这是虽然基本上都完成了题目,但是队内的共识还是觉得这次完成的不够好,所以我专门做了一次关于这次数模比赛的复盘,希望能够有所收获。
源码在最后边。
题目简介
这次的A题是 分拣系统优化问题。
问题背景
电商公司配送中心的工作流程中,分拣环节的是影响配送中心整体性能的关键因素。
系统的流程如下
首先,系统统计汇总出当天全部待配送订单所包含的所有货品及相应数量。然后,转运工将这些货品由仓库转运至分拣处,并放置到货架上,等待分拣。而问题也做了简化,不需要考虑货架的承载量,一个货架只放置一种货品,对件数没有限制。最后,分拣工按任务单依次分拣出每一个订单的货品。
而题目就是在这样的背景下,需要我们对分拣系统做优化。
其实这个背景就划分了流程:分批、上架、分拣。
而下面的题目也是这样。
题目以及思路
具体题目和数据可以直接去官网查看“华中杯”大学生数学建模挑战赛 (hzbmmc.com)
分批算法设计
我们需要设计一个算法,实现将订单分批。货架的个数有限,而且每一个货架只能放置一种货物,当订单全部的货物总数超过货架数时,需要对订单进行分批。
算法的结果,需要计算附件中订单的信息在货架总数N为200时,输出最少的批次数,和分批中每批的订单数、货品种类数等信息。
MindMap
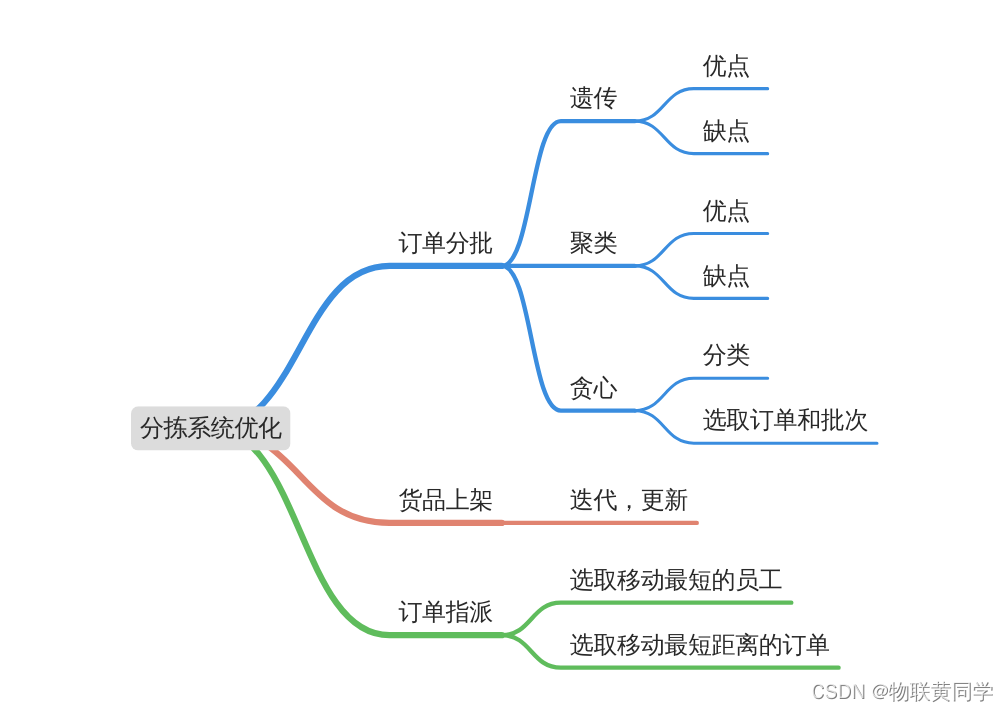
相信看完这道题目,很多人和我一样想到了遗传算法和聚类算法。的确遗传算法是适合寻求最优解、而聚类算法则是很适合利用样本空间中样本的相似度进行聚类。
而以下就是我对基于该题目遗传和聚类的分析。
遗传算法优缺点
优点
遗传算法的优点在于可以通过不断的迭代,筛选出优秀基因,针对这道题,我觉得其实就是筛选出优秀的订单的分批。
缺点
但是不同的是,我们在遗传算法的过程中,是有基因交换和基因变异两种情况的,这是遗传算法的筛选的途径。但是基因交换时,是将相同的位置(相对)的染色体进行交换,而我们如果是将不同批次的订单拆分后需要考虑的是交换后的新增种类数,而不是长度,所以单纯的遗传不一定适合。
聚类算法优缺点
优点
可以有效地将数据进行归类聚集。
缺点
就本题而言,聚类本身依靠的样本数据地相似程度,而该题需要的是新增种类,这显然不是可以通过改变相似程度的衡量方式可以处理的。直接聚类的结果可能会使得每个类都很聚集,但是不能使得类充分接近甚至达到货品种类数N的情况。
结合这两种算法,我提出了一种较为朴素的分批算法模型,算法的内核是贪心思想。
基于贪心的分批算法
分批过程,可以参考下图。
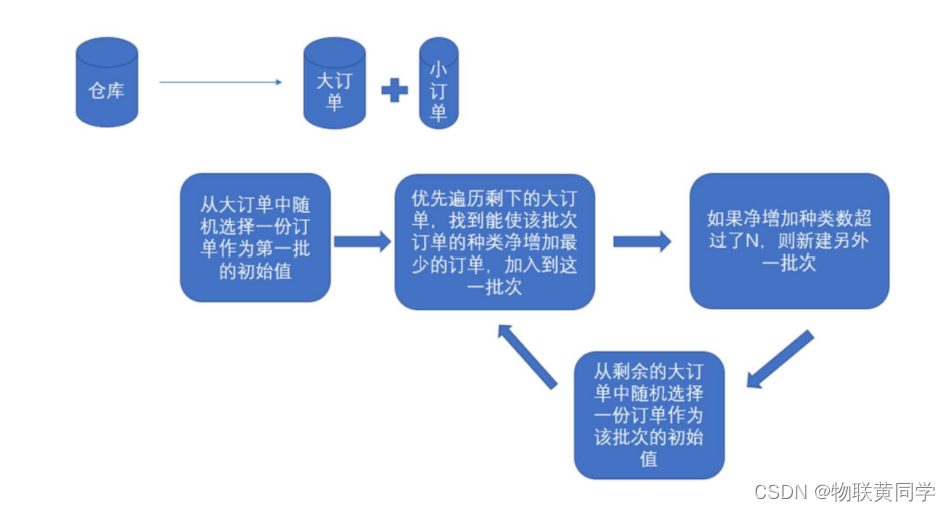
图片来自于我的队友(太强了,吹吹我的队友)
我们可以先将所有的订单按照种类数进行分类,划分大小订单。然后是根据大小订单,先用大订单快速生成批次,然后再从小订单中将订单加入批次。
关于这个模型,有几个重点。
订单加入批次——贪心
无论是大订单还是小订单,都先从已有的批次中选取可以添加当前订单且加入后批次新增种类数最小,这就是一个 贪心 的体现。
先大后小
我们在该模型中提出,需要先从大订单中选取,然后再选取小订单,为什么这样呢?
原因很简单,大订单因为自身货品的种类数较多,所以彼此之间种类的差异度会较大,我们可以利用这种特性,快速生成较多的批次,同时又能够使得生成的批次中种类的数量较多。
货品上架——遗传、贪心
在分好批次之后,针对每个批次,我们需要确定批次中货品的种类的上架顺序,根据每个订单的货品种类在该批次中的最大最小次序,有下列关于订单的拣选距离定义公式
我们需要设计出算法,使得批次中订单拣选距离的总和尽可能小。
我们参考了遗传算法中的基因交换的思路,我们先将批次中的货品的种类任意排序,然后经过多次迭代,每次迭代的过程:随机选取两个种类,如果种类交换次序后,批次中订单拣选距离相比原来拣选距离更小,我们就更新为新的次序。这里其实也用了贪心的思想,每次迭代保存局部最优解,然后用局部最优解去逼近全局最优解。
订单指派算法——贪心、并行分配
在分批、上架完成之后,我们需要对分拣工进行订单的指派,目的是使完成的时间尽可能小,每个分拣工的距离尽可能均衡。需要求取的结果是分拣工人数为5的时候的结果。
我们的算法是在每次优先选取移动距离最小的员工进行指派,然后优先选取Ta最近的订单,进行分配。
首先选取移动距离最小的员工这一点很好理解,因为该员工是所有员工中最先完成,所以需要优先分配,然后为了减少不必要的移动距离,需要给ta 分配最近的订单。
Code(Python)
import random
import pandas as pd
import time
# 这里定义一个全局变量,用来表示最大的货架数——即批次种类限制
N = 200
# 然后是写一个函数,实现只存储同一订单对应的货品种类
def big_and_small(choose0, order):
"""
该函数用于在未保留的订单中划分大订单和小订单,大订单占1/3
:param choose0:
:param order:
:return:
"""
big1 = []
small0 = []
choose0 = dict(choose0)
# 选取的订单字典,键是订单号,值是种类数
choose_order = {}
for i1 in choose0:
if choose0[i1] == 0:
choose_order[i1] = len(order[i1])
# 将未被选的订单字典排序
choose_order = sorted(choose_order.items(), key=lambda x: x[1])
new_len = len(choose_order)
# 计算大小分界的索引
mid_index = new_len * 2 // 3
index0 = 0
for i1 in choose_order:
if index0 < mid_index:
small0.append(i1[0])
else:
big1.append(i1[0])
index0 += 1
return big1, small0
# 写一个函数判断是否在当前批次
def is_in(batch, order):
"""
其实应该是得出新增订单的新增货品种类数
:param batch: 当前批订单, 内容是包含的货品
:param order: 当前订单,也是货品
:return: 新增货品种类数
"""
# 将批次和订单都列表化
batch = list(batch)
order = list(order)
ans = 0
# 循环累加不在当前批次的货品种类数
for o0 in order:
if o0 not in batch:
ans += 1
return ans
# 写一个选取函数
def choose_batch(orders1, batch01, batch02, keys0):
"""
该函数用于在大订单集或者小订单集将这些订单实现分批
引入洗牌算法,将选取的订单的顺序进行打乱随机
:param orders1: 订单
:param batch01: 批次列表1,存储批次对应的订单
:param batch02: 批次列表2,存储批次对应的货品种类
:param keys0: 选取订单的列表, 内容是订单号
:return: 返回选取加入后的批次1和2
"""
# 写一个洗牌算法
# 先获取选取订单的长度
# keys_len = len(keys0)
# # 逆序遍历选取列表
# # 通过交换随机下标来实现将选取的订单的顺序洗牌
# for k in range(keys_len - 1, -1, -1):
# # 获取随机下标
# rindex = random.randint(0, k)
# # 交换位置
# temp = keys0[rindex]
# keys0[rindex] = keys0[k]
# keys0[k] = temp
batch1 = dict(batch01)
batch2 = dict(batch02)
# 获取到当前最大批次数对应的下标
i0 = len(batch1) - 1
# 如果此时没有,这需要置为0
if i0 < 0:
i0 = 0
for key0 in keys0:
# 初始时需要创建批次
if i0 not in batch1:
batch1[i0] = []
batch2[i0] = []
add_type = -1
index0 = -1
flag = False
for j in range(i0 + 1):
if key0 in batch1[j]:
flag = True
break
at = is_in(batch2[j], orders[key0])
# 完全重合直接退出循环
if at == 0:
index0 = j
break
if (add_type < 0 or add_type >= at) and len(batch2[j]) + at <= N:
add_type = at
index0 = j
if flag:
continue
if index0 >= 0:
batch1[index0].append(key0)
for good in orders1[key0]:
if good not in batch2[index0]:
batch2[index0].append(good)
else:
i0 += 1
batch1[i0] = []
batch1[i0].append(key0)
batch2[i0] = orders1[key0]
return batch1, batch2
# 然后接下来写一个从小订单中选取
def choose_small(orders1, batch1, batch2, small1):
orders1 = dict(orders1)
keys = list(small1)
batch1 = dict(batch1)
batch2 = dict(batch2)
batch1, batch2 = choose_batch(orders1, batch1, batch2, keys)
return batch1, batch2
# 这个是在大的数组中重新选取
def choose_big(big1, orders1, batch, batch2):
orders1 = dict(orders1)
keys = list(big1)
# 批次数组有两种,一种是存储订单,一种是存储货品
batch1 = dict(batch)
batch2 = dict(batch2)
batch1, batch2 = choose_batch(orders1, batch1, batch2, keys)
return batch1, batch2
# 然后写一个迭代函数
def gen_ite(order, btch_1, btch_2):
"""
参考遗传算法的精英基因保留的思想,我们在迭代的过程中将批次中订单数较多的保留,这里每次选取10%的批次
然后需要将这些批次标记为已经选择然后重新在为选取的订单集划分大小订单
选取的批次可以直接新增在下一代的开头
:param order: 订单字典,订单号对应相应的货品种类
:param btch_1:
:param btch_2:
:return: 最终多次迭代后的结果
"""
btch_1 = dict(btch_1)
btch_2 = dict(btch_2)
for i0 in range(1):
# 先对批次的订单数排序 —— 降序排序
btch = sorted(btch_1.items(), key=lambda x: len(x[1]), reverse=True)
btch_len = len(btch)
index0 = btch_len // 5
# 生成两个新的字典,和btch1,2类似
bt1 = {}
bt2 = {}
# 先将精英保留
# 选择字典
choose_0 = {}
for j in order.keys():
choose_0[j] = 0
for k in range(index0):
for o0 in btch_1[k][1]:
choose_0[o0] = 1
bt1[k] = btch_1[btch[k][0]]
bt2[k] = btch_2[btch[k][0]]
keys = []
for m in order.keys():
if choose[m] == 0:
keys.append(m)
# # 接下来划分大小订单
# big1, small1 = big_and_small(choose, orders)
# print('big: %d small: %d' % (len(big1), len(small1)))
# # 之后根据划分的大小订单在得到新的分批
# bt1, bt2 = choose_big(big1, orders, bt1, bt2)
# print(len(bt1), len(bt2))
# # bt1, bt2 = choose_small(orders, bt1, bt2, small1)
# # print(len(bt1), len(bt2))
bt1, bt2 = choose_batch(order, bt1, bt2, keys)
# 然后比较新旧分批的批数来更新批次
if len(bt1) < len(btch_1):
btch_1 = bt1
btch_2 = bt2
print('第%d次, 批次数为%d' % (i0 + 1, len(btch_1)))
le = 0
for bi in btch_1:
le += len(btch_1[bi])
print(le)
return btch_1, btch_2
# 写一个计算距离的函数
def compute_dis(order, batch10, goods):
"""
:param order: 其实就是订单集合,通过订单可以知道需要的货品
:param batch10: 批次下的订单列表
:param goods: 当前批次下的货物关于货物列表的索引
:return: 返回距离和
"""
order = dict(order)
batch10 = list(batch10)
goods = dict(goods)
dis = 0
for bat in batch10:
index_max = -1
index_min = -1
for good in order[bat]:
if index_min == -1 and index_max == -1:
index_max = index_min = goods[good]
else:
index_max = max(index_max, goods[good])
index_min = min(index_min, goods[good])
dis += index_max - index_min
return dis
# 写一个第二问的解决函数
def solution2(order, batch2, batch1):
batch1 = dict(batch1)
batch2 = dict(batch2)
order = dict(order)
pre_total = 0
ans = []
p = 0
total = 0
start0 = time.time()
for batch in batch2.items():
# 现在是对每一个批次
# 先建立货物种类到下标映射, 和下标到货物的映射
good_to_index = {}
index_to_good = batch[1]
for index1 in range(len(index_to_good)):
good = index_to_good[index1]
good_to_index[good] = index1
dis = compute_dis(order, batch1[batch[0]], good_to_index)
print('当前第%d批原始距离为 %d' % (p + 1, dis))
pre_total += dis
for i0 in range(200000):
j = random.randint(0, len(index_to_good) - 1)
k = random.randint(0, len(index_to_good) - 1)
if j == k:
continue
# 获取货物信息
good1, good2 = index_to_good[j], index_to_good[k]
# 先交换
temp = good_to_index[good1]
good_to_index[good1] = good_to_index[good2]
good_to_index[good2] = temp
if dis > compute_dis(order, batch1[batch[0]], good_to_index):
index_to_good[j], index_to_good[k] = good2, good1
dis = compute_dis(order, batch1[batch[0]], good_to_index)
else:
good_to_index[good1], good_to_index[good2] = good_to_index[good2], good_to_index[good1]
print('迭代后 第%d批原始距离为 %d' % (p + 1, dis))
total += dis
ans.append(index_to_good)
p += 1
print('原始距离', pre_total)
print('最终距离', total)
end0 = time.time()
print('时间消耗', end0 - start0)
return ans
# 找到订单的起始点
def find_min_and_max_index(order_good, good_index):
order_good = list(order_good)
good_index = dict(good_index)
min_index = max_index = -1
for good_name in order_good:
if min_index == -1 and max_index == -1:
min_index = max_index = good_index[good_name]
continue
min_index = min(min_index, good_index[good_name])
max_index = max(max_index, good_index[good_name])
return min_index, min_index
def right_find(order, batch1, good_index, pos):
order = dict(order)
batch1 = list(batch1)
good_index = dict(good_index)
ans = ''
j = int(pos)
tar = j
for name in batch1:
i1, i2 = find_min_and_max_index(order[name], good_index)
if i1 >= pos and (j > i1 or j == pos):
j = i1
ans = name
tar = i2
return ans, tar
def left_find(order, batch1, good_index, pos):
order = dict(order)
batch1 = list(batch1)
good_index = dict(good_index)
ans = ''
j = pos
tar = j
for name in batch1:
i1, i2 = find_min_and_max_index(order[name], good_index)
if i1 <= pos and (j < i1 or j == pos):
j = i2
ans = name
tar = i1
return ans, tar
def find_people(distance):
"""
找工人函数
我们根据方向和工人所处的位置决定,选取哪个工人
:param distance: 距离数组
:return: 返回工人的下标
"""
# 答案初始化为下标0
ans = 0
distance = list(distance)
for i1 in range(1, len(distance)):
if distance[i1] < distance[ans]:
ans = i1
return ans
def solution3(order, batch1, batch2, n):
"""
该函数主要用于求解第三问
:param order: 订单对应的货品,字典对象
:param batch1: 分批好的订单,批号对应的订单
:param batch2: 分批好的订单对应的货品种类,批号对应的种类
:param n: 工人的数量
:return: 返回第三问需要的结果
"""
# 先将这些字典对象示例化,实现可变参数在函数内和外的分离
batch1 = dict(batch1)
order = dict(order)
batch2 = dict(batch2)
# 答案,用列表存储,每一个其实也是列表,分别对应答案需要的答案
ans = []
peo_dis1 = [] # 用来计算每一批员工的总路程
total_dis0 = [] # 总距离
for i1 in range(n):
total_dis0.append(0)
# 我们遍历批次
for i1 in batch1.keys():
# 实例化批次对应的订单和货品种类,这里其实还是将其变为数组的形式
bat_or = list(batch1[i1])
bat_go = list(batch2[i1])
# 货品在该批次中对应的位置, 即货架的位置
good_index = {}
# 遍历一遍订单和货品种类,这里的顺序其实就是第二问求解的摆放顺序
for ind in range(len(bat_go)):
# 先获取当前的货物
good = bat_go[ind]
# 利用字典的映射关系,设置货物对应的摆放位置的关系
good_index[good] = ind
people = [] # 工人列表,用来存储工人的位置
task = [] # 任务列表,用来存储工人当前批干的第几个订单
peo_dis0 = [] # 当前批的距离
# 先将这两个列表都初始化为0
for p in range(n):
people.append(0)
task.append(0)
peo_dis0.append(0)
# 当批次中的订单还有的时候,需要进行分配
while len(bat_or) > 0:
# 我们可以先进行正向的寻找, 先找当前最小的下标,同级优先按工人编号寻找
p = find_people(peo_dis0)
# 获取当前工人的位置
pos = people[p]
# 然后在以当前工人位置为起点,向右寻找最近的订单,并返回订单号和订单完成时工人的位置
name, next_pos = right_find(order, bat_or, good_index, pos)
# 如果找不到订单,说明右边没有订单了,需要逆向寻找
if name == '':
# 向当前位置最左边找离最近的订单
name, next_pos = left_find(order, bat_or, good_index, pos)
task[p] += 1 # 当前工人的任务数 + 1
temp = [name, i1 + 1, p + 1, task[p]] # 当前行的答案
ans.append(temp) # 将这一行的答案添加到最终答案中
bat_or.remove(name) # 将这个订单从列表中移除
print(next_pos)
# 计算移动距离
dis = abs(pos - next_pos)
# 加和
peo_dis0[p] += dis
people[p] = next_pos
peo_dis1.append(peo_dis0)
for ik in range(n):
total_dis0[ik] += peo_dis0[ik]
# 返回答案
return ans, peo_dis1, total_dis0
if __name__ == "__main__":
start = time.time()
# 先写一个文件路径
filepath = '附件1:订单信息.csv'
# 先读取文件
# 使用 pandas 内置的读取方式
df = pd.read_csv(filepath) # 将文件读取为一个dataframe格式
con = pd.DataFrame(df, columns=['OrderNo', 'ItemNo'])
orders = {}
for line in con.index:
if not con.iloc[line]['OrderNo'] in orders:
orders[con.iloc[line]['OrderNo']] = []
orders[con.iloc[line]['OrderNo']].append(con.iloc[line]['ItemNo'])
s = set(orders.keys())
print(len(s))
# 选取字典,表示对应订单是否被选取
choose = {}
# 初始化为未被选取
for key in orders.keys():
choose[key] = 0
big, small = big_and_small(choose, orders)
print(len(big), len(small))
b1, b2 = choose_big(big, orders, {}, {})
b1, b2 = choose_small(orders, b1, b2, small)
end = time.time()
print(end - start)
print(len(b1), len(b2))
btch1, btch2 = dict(b1), dict(b2)
file = open('result1.csv', 'w+')
result1 = 'OrderNo,GroupNo\n'
for b in btch1.keys():
for o in btch1[b]:
result1 += o + ',' + str(b + 1) + '\n'
print(result1, file=file)
file.close()
ans2 = solution2(orders, batch1=btch1, batch2=btch2)
result2 = 'ItemNo,GroupNo,ShelfNo\n'
for index in btch2.keys():
btch2[index] = ans2[index]
for _i in range(len(ans2[index])):
result2 += ans2[index][_i] + ',' + str(index + 1) + ',' + str(_i + 1) + '\n'
file = open('result2.csv', 'w+')
print(result2, file=file)
file.close()
ans3, peo_dis, total_dis = solution3(orders, batch2=btch2, batch1=btch1, n=5)
result3 = 'OrderNo,GroupNo,WorkerNo,TaskNo\n'
for a in ans3:
for index in range(len(a)):
result3 += str(a[index])
if index + 1 < len(a):
result3 += ','
else:
result3 += '\n'
file = open('result3.csv', 'w+')
print(result3, file=file)
file.close()
result4 = ''
for b in peo_dis:
for index in range(len(b)):
result4 += str(b[index])
if index + 1 < len(b):
result4 += ','
else:
result4 += '\n'
file = open('员工路程,单批.csv', 'w+')
print(result4, file=file)
file.close()
file = open('员工路径总和.csv', 'w+')
result4 = ''
for i in range(len(total_dis)):
result4 += str(total_dis[i])
if i + 1 < len(total_dis):
result4 += ','
else:
result4 += '\n'
print(result4, file=file)
file.close()
总结
这次其实可以优化的地方蛮多的,比如第一问其实可以使用遗传算法进行优秀批次的保留,然后不断筛选(可是我在实践编程中,出了bug没有实现成功)。
