基于选择性卷积特征的广义均值池化细粒度图像检索
paper题目:Selective Convolutional Features based Generalized-mean Pooling for Fine-grained Image Retrieval
paper是上海交通大学发表在VCIP 2018的工作
paper地址:链接
Abstract
使用卷积神经网络(CNN)进行图像检索已经获得了很多关注。本文专注于一项更具挑战性的任务:细粒度图像检索。提出了一种使用广义均值池(GeM pooling)的简单有效的特征聚合方法,它可以更好地利用来自卷积层输出张量的信息。此外,提出了一种简单的特征选择方案来去除噪声和背景。实验结果表明,本文的聚合方法不仅优于一般图像检索的状态聚合方法,而且达到了与现有细粒度图像检索聚合方法相同的水平,具有更紧凑的表示和更少的内存成本。
关键词——特征选择、广义平均池化、细粒度图像检索。
I. INTRODUCTION
细粒度图像分析是近年来计算机视觉领域非常热门的研究课题。细粒度图像检索的概念由Xie[1]在 2015 年首次提出。如图 1 所示,与一般图像检索任务不同,细粒度图像检索任务的难点在于细微差别。此外,虽然图像属于同一类别,但它们在形式、姿势、颜色和背景上可能存在很大差异。

图 1. 细粒度图像检索与一般图像检索
随着深度学习方法在计算机视觉任务上的成功,对于基于卷积神经网络(CNN)的一般图像检索,sum-pooling 及其改进形式已被证明比 max-pooling(Maximum Activation of Convolutions,MAC ),例如SPoC、CroW和R-MAC。 SPoC 已经证明,使用预先训练的 CNN 模型进行检索,卷积层上的简单空间和池化优于全连接层。此外,可以通过应用具有中心先验的简单空间高斯加权方案来增强这种表示的性能。 CroW不仅考虑了空间权重取决于图像内容,还考虑了通道权重,这是一种比固定中心先验方法更有效的方法。 R-MAC采用滑动窗口方法,通过在每个特定区域内执行空间最大池化来生成一组区域向量,并通过和池化将生成区域的向量聚合为单个表示。
SCDA是第一个用于细粒度图像检索的聚合方法。为了去除背景和噪声,SCDA提出在深度方向对卷积特征图 ( H × W × K ) (H \times W \times K) (H×W×K)求和,得到一个聚合特征图 ( H × W × 1 ) (H \times W \times 1) (H×W×1)。然后可以计算所有 H × W H \times W H×W元素的平均值,用于选择描述符。聚合特征图中大于 m m m的元素位置的卷积特征被保留,小于 m m m的被丢弃。此外,SCDA 还使用最大连通面积算法和与Relu5_2层的交集来进一步减少描述符的数量。剩余的深度局部描述符分别通过averagepooling和max-pooling聚合,然后连接形成最终的图像表示。
对于细粒度的图像检索任务,虽然 SCDA 的性能优于为一般图像检索任务而设计的基于 CNN 的最先进的特征聚合方法,但它仍然存在一些问题。首先,结合不同层的输出和翻转图像,其最终的图像表示可以达到 4096 维,不够紧凑。即使通过 PCA 或 SVD 可以减少表示向量的长度,也会冒降低检索性能的风险。其次,SCDA 使用全局最大池化和平均池化,没有充分利用所选深度描述符的信息。
为了解决上述问题,提出了一种基于选择性卷积特征的广义平均池化方法,称为SGeM。 SGeM简单且无监督,仅使用全连接层之前的最后一个卷积层的特征图。 SGeM用广义平均池化代替了全局最大池化和平均池化,这是最大池化和平均池化的一般形式。此外,设计了一种新的特征选择方案,通过计算特征图的每个位置达到最大激活的频率并设置适当的阈值来选择局部描述符。本文的主要贡献总结如下:(1)对于细粒度的图像检索任务,实验证明了广义平均池化优于最大池化和平均池化,这是一种竞争性聚合方法。 (2) 提出了一种新的特征选择方案,可以进一步提高检索性能。 (3) 大量实验表明,本文的方法可以达到甚至优于最先进的方法,具有更紧凑的表示 (512D)。
II. APPROACH
A. Local CNN features
考虑一个没有全连接层的预训练 CNN。给定输入图像,卷积层的 3D 激活大小为 W × H × K W \times H \times K W×H×K,其中 K K K是特征图的数量, W × H W \times H W×H是特征图的空间分辨率。将这个响应的 3D 张量视为一组 ( W × H ) (W \times H) (W×H)局部描述符,位置 ( i , j ) (i, j) (i,j)处的每个局部描述符 I i , j I_{i, j} Ii,j?是一个 K K K维向量。换句话说, ( W × H ) (W \times H) (W×H)空间网格上的每个位置都是局部描述符的位置。将 F k \mathscr{F}^{k} Fk表示为第 k k k个特征图,它的大小也是 ( W × H ) (W \times H) (W×H)。请注意,在方法中选择了最后一个卷积层。
B. Feature Selection Scheme
在 CNN 特征张量中,每个特征图都可以作为一个滤波器张量的处理结果。如果最大激活出现在特征图的位置 ( i , j ) (i, j) (i,j),可以认为这个过滤器对原始图像的相应部分最感兴趣。从图 2 可以看出,第 27 个特征图的最大激活值对应于鸟的眼睛,第 181 个和第 433 个特征图的最大激活值分别对应于白色和棕色羽毛的边缘。
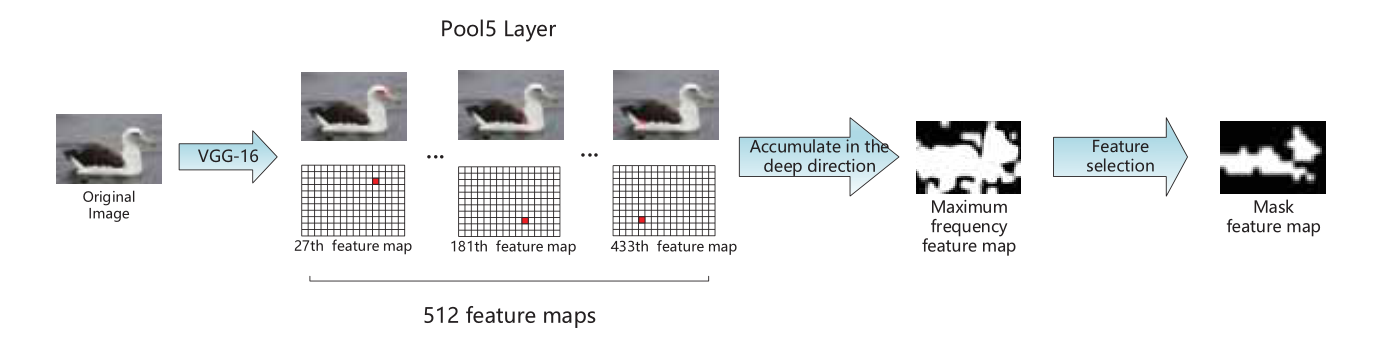
图 2. 提出的特征选择方案。网格中的红色块是特征图中最大激活的位置。而图像中的红色是红色块的对应部分。
基于这一观察,提出了一种简单的特征选择方案,计算特征图每个位置的最大激活频率。假设输入 VGG-16 网络的图像。它的 pool5 层的输出张量大小为 512 × W × H 512 \times W \times H 512×W×H。最大激活出现在 ( i , j ) (i, j) (i,j)处的次数越多,局部描述符 I i , j I_{i, j} Ii,j?越有用。
然后在深度方向对所有的特征图
(
H
×
W
×
K
)
(H \times W \times K)
(H×W×K)求和,然后得到一个最大频率特征图
(
H
×
W
×
1
)
(H \times W \times 1)
(H×W×1)。在这个 2D map中,每个位置的平均最大激活出现次数在公式 1 中给出。注意
K
/
(
W
×
H
)
K /(W \times H)
K/(W×H)是参考值,在实验中尝试不同的值来研究其对检索性能的影响。
?Threshold?
=
K
/
(
W
×
H
)
(
1
)
\text { Threshold }=K /(W \times H) \quad(1)
?Threshold?=K/(W×H)(1)
而这个值是选择有用描述符的关键。需要保留最大频率图中大于 Threshold 的元素位置的局部描述符,其余的则丢弃。这种方法的直观解释是细粒度对象的位置似乎对卷积特征张量的大多数特征图都有响应。最后得到了掩码特征图,如公式 2 所示。整个特征选择方案如图 2 所示。
Mask
?
i
,
j
=
{
1
F
r
e
i
,
j
≥
?Threshold?
0
?otherwise?
(
2
)
\operatorname{Mask}_{i, j}=\left\{\begin{array}{rr} 1 & F_{r} e_{i, j} \geq \text { Threshold } \\ 0 & \text { otherwise } \end{array}\right. \quad(2)
Maski,j?={10?Fr?ei,j?≥?Threshold??otherwise??(2)
C. Generalized-mean Pooling
global max-pooling 和 sum-pooling 常被用作图像检索的基本聚合方法,分别表示为 Eq 3 和 Eq 4。与 SCDA 相比,maxpooling 仍然是一种有效的方法。但是,最大池化和总和池化有其缺点。 Max-pooling 只计算每个特征图的最大值,可能会丢失其他激活的信息。 Sum-pooling 或 averagepooling 平均每个特征图的所有激活,这也会削弱最终表示的判别力。
I
M
a
x
=
[
f
1
(
m
)
…
f
i
(
m
)
…
f
K
(
m
)
]
T
(
3
)
f
k
(
m
)
=
max
?
F
k
I
S
u
m
=
[
f
1
(
s
)
…
f
i
(
s
)
…
f
K
(
s
)
]
T
(
4
)
f
k
(
s
)
=
∑
F
k
\begin{array}{r} I_{M a x}=\left[f_{1}^{(m)} \ldots f_{i}^{(m)} \ldots f_{K}^{(m)}\right]^{T}\quad(3) \\ f_{k}^{(m)}=\max \mathscr{F}^{k} \\ I_{S u m}=\left[f_{1}^{(s)} \ldots f_{i}^{(s)} \ldots f_{K}^{(s)}\right]^{T} \quad(4)\\ f_{k}^{(s)}=\sum \mathscr{F}^{k} \end{array}
IMax?=[f1(m)?…fi(m)?…fK(m)?]T(3)fk(m)?=maxFkISum?=[f1(s)?…fi(s)?…fK(s)?]T(4)fk(s)?=∑Fk?
因此,利用广义均值池化来代替最大池化和总和池化。从 Eq 5 可以看出,maxpooling 和 sum-pooling 是 GeM pooling 的特例。
当
p
→
+
∞
p \rightarrow+\infty
p→+∞时,GeM pooling 变为 max-pooling。当
p
=
1
p=1
p=1时,GeM pooling变成average-pooling(注意所有的特征向量都经过l2-normalization后处理,所以sum-pooling的结果等于average-pooling。接下来的部分,sum-pooling将代表 sumpooling 和 average-pooling)。当
p
p
p从 1 变化到
+
∞
+\infty
+∞时,可能存在最优值。最终的特征向量由具有广义均值激活的每个特征图的单个值组成,其维数等于
K
K
K,这使其成为紧凑的图像表示。注意,仅将所选描述符的元素考虑到 GeM 池化的计算中。
I
G
e
M
=
[
f
1
(
g
)
…
f
i
(
g
)
…
f
K
(
g
)
]
T
f
k
(
g
)
=
(
1
∣
∑
F
k
∣
∑
x
∈
F
k
x
p
)
1
p
(
5
)
\begin{gathered} I_{G e M}=\left[f_{1}^{(g)} \ldots f_{i}^{(g)} \ldots f_{K}^{(g)}\right]^{T} \\ f_{k}^{(g)}=\left(\frac{1}{\left|\sum \mathscr{F}^{k}\right|} \sum_{x \in \mathscr{F}_{k}} x^{p}\right)^{\frac{1}{p}} \end{gathered}\quad(5)
IGeM?=[f1(g)?…fi(g)?…fK(g)?]Tfk(g)?=(∣∑Fk∣1?x∈Fk?∑?xp)p1??(5)
D. Combining different Threshold
为了进一步增强特征表示的辨别力,结合了两个不同的Threshold。这两个阈值是接近
K
/
(
W
×
H
)
K /(W \times H)
K/(W×H)的两个整数。它们的关系在公式 6 中给出。
T
h
r
e
s
h
o
l
d
1
<
K
/
(
W
×
H
)
<
T
h
r
e
s
h
o
l
d
2
(
6
)
Threshold 1< K /(W \times H)< Threshold 2 \quad(6)
Threshold1<K/(W×H)<Threshold2(6)
将
I
G
e
M
+
I_{G e M}+
IGeM?+表示为结合Threshold 1和Threshold 2的全局表示。此外,还结合了原始图像水平翻转的另一个
I
G
e
M
+
I_{G e M}+
IGeM?+,记为
I
G
e
M
?
f
l
i
p
(
512
D
)
.
I
G
e
M
+
I_{G e M_{-} f l i p}(512 D) . I_{G e M}+
IGeM??flip?(512D).IGeM?+ 和
I
G
e
M
?
f
l
i
p
+
I_{G e M_{-} f l i p}+
IGeM??flip?+在公式 7 中给出。这个版本的 SGeM 被称为
S
G
e
M
flip?
+
\mathrm{SGeM}_{\text {flip }}+
SGeMflip??+。
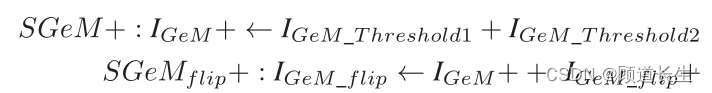
参考文献
[1] L. Xie, J. Wang, B. Zhang, and Q. Tian, “Fine-grained image search,” IEEE Transactions on Multimedia, vol. 17, no. 5, pp. 636–647, 2015.
