1 RNN 的缺点
??我在上一篇博客中跟大家一步一步探索了 RNN 模型的网络结构,最后面也介绍了 RNN 的应用场景。但在实际应用中,标准 RNN 训练的优化算法面临一个很大的难题,就是长期依赖问题——由于网络结构的变深使得模型丧失了学习到先前信息的能力,通俗的说,标准的 RNN 虽然有了记忆,但很健忘,也即标准 RNN 只有短时记忆。循环神经网络在处理较长的句子时,往往只能够理解有限长度内的信 息,而对于位于较长范围类的有用信息往往不能够很好的利用起来。我们把这种现象叫做短时记忆。
??针对标准 RNN 短时记忆的问题,最直接的想法就是延长这种短时记忆,使得 RNN 可以有效利用较大范围内的训练数据,从而提升性能。这时,一种基于 RNN 改进的新型网络模型——LSTM 该登场了。同时在上篇博客的最后面谈到了 RNN 的梯度消失问题,LSTM 模型可以有效地解决这个问题。
2 LSTM
??1997 年,瑞士人工智能科学家 Jürgen Schmidhuber 提出了 长短时记忆网络(Long Short-Term Memory,简称 LSTM)。LSTM 相对于基础的 RNN 网络来说,记忆能力更强,更擅长处理较长的序列信号数据,LSTM 提出后,被广泛应用在序列预测、自然语言处理等任务中,几乎取代了基础的 RNN 模型。
??首先回顾一下基础的 RNN 网络结构:
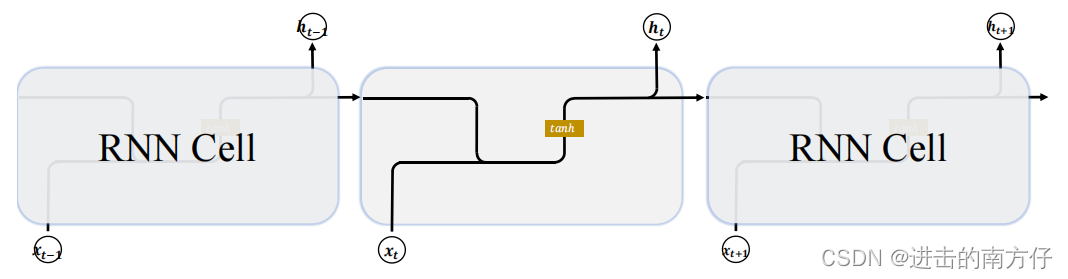
上一个时间戳的状态向量
h
t
?
1
\boldsymbol{h_{t-1}}
ht?1? 与当前时间戳的输入
x
t
\boldsymbol{x_t}
xt? 经过线性变换后,通过激活函数
t
a
n
h
\boldsymbol{tanh}
tanh 后得到新的状态向量
h
t
\boldsymbol{h_{t}}
ht?。相对于基础的 RNN,网络只有一个状态向量
h
t
\boldsymbol{h_{t}}
ht?,LSTM 新增了一个状态向量
C
t
\boldsymbol{C_{t}}
Ct?,同时引入了 门控(Gate)机制,通过门控单元来控制信息的遗忘和刷新: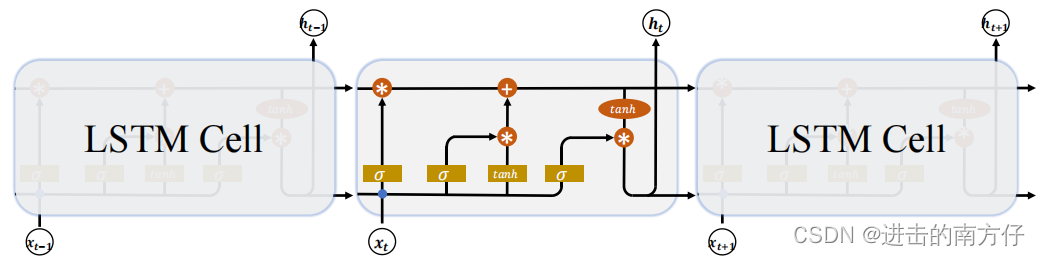
??在 LSTM Cell 中,有两个状态向量
c
\boldsymbol{c}
c 和
h
\boldsymbol{h}
h,其中
c
\boldsymbol{c}
c 作为 LSTM 的内部状态向量,可以理解为 LSTM 的 内存状态向量 Memory,而
h
\boldsymbol{h}
h 表示 LSTM 的输出向量。相对于基础的 RNN 来说,LSTM 把内部 Memory 和输出分开为两个变量,同时利用三个门控:输入门(Input Gate)、遗忘门(Forget Gate)和输出门(Output Gate)来控制内部信息的流动。
??门控机制可以理解为控制数据流通量的一种手段,类比于水阀门:当水阀门全部打开时,水流畅通无阻地通过;当水阀门全部关闭时,水流完全被隔断。在 LSTM 中,阀门开和程度利用门控值向量
g
\boldsymbol{g}
g 表示:

上图中通过
σ
(
g
)
\boldsymbol{\sigma(g)}
σ(g) 激活函数将门控值压缩到
[
0
,
1
]
\boldsymbol{[0, 1]}
[0,1] 之间,当
σ
(
g
)
=
0
\boldsymbol{\sigma(g) = 0}
σ(g)=0 时,门控全部关闭,输出
o
=
0
\boldsymbol{o = 0}
o=0;当
σ
(
g
)
=
1
\boldsymbol{\sigma(g) = 1}
σ(g)=1 时,门控全部打开,输出
o
=
x
\boldsymbol{o = x}
o=x。通过门控机制可以较好地控制数据的流量程度。
注:到此您可以跳转至 3 GUR 阅读完 GUR 的原理之后再回来阅读 LSTM,因 GUR 结构较为简单。
2.1 遗忘门
??遗忘门作用于 LSTM 状态向量 c \boldsymbol{c} c,用于控制上一个时间戳的记忆 c t ? 1 \boldsymbol{c_{t - 1}} ct?1? 对当前时间戳的影响。

遗忘门的控制变量
g
f
\boldsymbol{g_f}
gf? 计算过程如下:
g
f
=
σ
(
W
f
[
h
t
?
1
;
x
t
]
+
b
f
)
\boldsymbol{g_f = \sigma(W_f[h_{t- 1};x_t]+b_f)}
gf?=σ(Wf?[ht?1?;xt?]+bf?)
其中
W
f
\boldsymbol{W_f}
Wf? 和
b
f
\boldsymbol{b_f}
bf? 为遗忘门的参数张量,可由反向传播算法自动优化,
σ
\boldsymbol{\sigma}
σ 为激活函数,一般使用 Sigmoid 函数。当
g
f
=
1
\boldsymbol{g_f = 1}
gf?=1 时,遗忘门全部打开,LSTM 接受上一个状态
c
t
?
1
\boldsymbol{c_{t-1}}
ct?1? 的所有信息 ;当
g
f
=
0
\boldsymbol{g_f = 0}
gf?=0 时,遗忘门关闭,LSTM 直接忽略
c
t
?
1
\boldsymbol{c_{t-1}}
ct?1? 的所有信息输出为 0 的向量。这也是遗忘门的名字由来。经过遗忘门后,LSTM 的状态向量
c
t
\boldsymbol{c_t}
ct? 变为
g
f
c
t
?
1
\boldsymbol{g_fc_{t-1}}
gf?ct?1?。
2.2 输入门
??输入门用于控制 LSTM 对输入的接收程度。

首先通过对当前时间戳的输入
x
t
\boldsymbol{x_t}
xt? 和上一个时间戳的输出
h
t
?
1
\boldsymbol{h_{t - 1}}
ht?1? 做非线性变换得到新的输入向量
c
t
~
\boldsymbol{\tilde{c_t}}
ct?~?:
c
t
~
=
t
a
n
h
(
W
c
[
h
t
?
1
;
x
t
]
+
b
c
)
\boldsymbol{\tilde{c_t} = tanh(W_c[h_{t -1};x_t] +b_c)}
ct?~?=tanh(Wc?[ht?1?;xt?]+bc?)
其中
W
c
\boldsymbol{W_c}
Wc? 和
b
c
\boldsymbol{b_c}
bc? 为输入门的参数,需要通过反向传播算法自动优化,
t
a
n
h
\boldsymbol{tanh}
tanh 为激活函数,用于将输入标准化到
[
?
1
,
1
]
\boldsymbol{[-1,1]}
[?1,1] 区间。
c
t
~
\boldsymbol{\tilde{c_t}}
ct?~? 并不会全部刷新进入 LSTM 的 Memory,而是通过输入门控制接受输入的量。输入门的控制变量同样来自于输入
x
t
\boldsymbol{x_t}
xt? 和输出
h
t
?
1
\boldsymbol{h_{t - 1}}
ht?1?:
g
i
=
σ
(
W
i
[
h
t
?
1
;
x
t
]
+
b
i
)
\boldsymbol{g_i = \sigma(W_i[h_{t - 1};x_t]+b_i)}
gi?=σ(Wi?[ht?1?;xt?]+bi?)
其中
W
i
\boldsymbol{W_i}
Wi? 和
b
i
\boldsymbol{b_i}
bi? 为输入门的参数,可由反向传播算法自动优化,
σ
\boldsymbol{\sigma}
σ 为激活函数,一般使用 Sigmoid 函数。输入门控制变量
g
i
\boldsymbol{g_i}
gi? 决定了 LSTM 对当前时间戳的新输入
c
t
~
\boldsymbol{\tilde{c_t}}
ct?~? 的接受程度:当
g
i
=
0
\boldsymbol{g_i = 0}
gi?=0 时,LSTM 不接受任何的新输入
c
t
~
\boldsymbol{\tilde{c_t}}
ct?~?;当
g
i
=
1
\boldsymbol{g_i = 1}
gi?=1 时,LSTM 全部接受新输入
c
t
~
\boldsymbol{\tilde{c_t}}
ct?~?。经过输入门之后,待写入 Memory 的向量为
g
i
c
t
~
\boldsymbol{g_i\tilde{c_t}}
gi?ct?~?。
??在遗忘门和输入门的控制下,LSTM 有选择地读取了上一个时间戳的记忆
c
t
\boldsymbol{c_t}
ct? 和当前时间戳的新输入
c
t
~
\boldsymbol{\tilde{c_t}}
ct?~?,状态向量
c
t
\boldsymbol{c_t}
ct? 的刷新方式为:
c
t
=
g
i
c
t
~
+
g
f
c
t
?
1
\boldsymbol{c_t = g_i\tilde{c_t} + g_fc_{t-1}}
ct?=gi?ct?~?+gf?ct?1?
得到的新状态向量
c
t
\boldsymbol{c_t}
ct? 即为当前时间戳的状态向量:

2.3 输出门
??LSTM 的内部状态向量 c t \boldsymbol{c_t} ct? 并不会直接用于输出,这一点和基础的 RNN 不一样。标准的 RNN 网络的状态向量 h t \boldsymbol{h_t} ht? 既用于记忆,又用于输出,所以基础的 RNN 可以理解为状态向量 c t \boldsymbol{c_t} ct? 和输出向量 h t \boldsymbol{h_t} ht? 是同一个对象。

在 LSTM 内部,状态向量并不会全部输出,而是在输出门的作用下有选择地输出。输出门的门控变量
g
o
\boldsymbol{g_o}
go?:
g
o
=
σ
(
W
o
[
h
t
?
1
;
x
t
]
+
b
o
)
\boldsymbol{g_o= \sigma(W_o[h_{t - 1};x_t]+b_o)}
go?=σ(Wo?[ht?1?;xt?]+bo?)
其中
W
o
\boldsymbol{W_o}
Wo? 和
b
o
\boldsymbol{b_o}
bo? 为输出门的参数,可由反向传播算法自动优化,
σ
\boldsymbol{\sigma}
σ 为激活函数,一般使用 Sigmoid 函数。当
g
o
=
0
\boldsymbol{g_o = 0}
go?=0 时输出关闭,LSTM 的内部记忆完全被隔断,无法用作输出,此时输出为 0 的向量;当
g
o
=
1
\boldsymbol{g_o = 1}
go?=1 时,输出完全打开,LSTM 的状态向量
c
t
\boldsymbol{c_t}
ct? 全部用于输出。LSTM 的输出为:
h
t
=
g
o
?
t
a
n
h
(
c
t
)
\boldsymbol{h_t = g_o\cdot tanh(c_t)}
ht?=go??tanh(ct?)
即内存向量
c
t
\boldsymbol{c_t}
ct? 经过 tanh 激活函数后与输入门作用,得到 LSTM 的输出。由于
𝒈
o
∈
[
0
,
1
]
\boldsymbol{ 𝒈_o ∈ [0,1]}
go?∈[0,1],
t
a
n
h
(
c
t
)
∈
[
?
1
,
1
]
\boldsymbol{tanh(c_t) ∈ [-1,1]}
tanh(ct?)∈[?1,1],因此 LSTM的输出
h
t
∈
[
?
1
,
1
]
\boldsymbol{h_t∈ [-1,1]}
ht?∈[?1,1]。
3.4 小结
??LSTM 虽然状态向量和门控数量较多,计算流程相对复杂。但是由于每个门控功能清晰明确,每个状态的作用也比较好理解。LSTM 的核心公式记录如下:
- 遗忘门: g f = σ ( W f [ h t ? 1 ; x t ] + b f ) \boldsymbol{g_f = \sigma(W_f[h_{t- 1};x_t]+b_f)} gf?=σ(Wf?[ht?1?;xt?]+bf?);
- 输入向量更新: c t ~ = t a n h ( W c [ h t ? 1 ; x t ] + b c ) \boldsymbol{\tilde{c_t} = tanh(W_c[h_{t -1};x_t] +b_c)} ct?~?=tanh(Wc?[ht?1?;xt?]+bc?);
- 输入门: g i = σ ( W i [ h t ? 1 ; x t ] + b i ) \boldsymbol{g_i = \sigma(W_i[h_{t - 1};x_t]+b_i)} gi?=σ(Wi?[ht?1?;xt?]+bi?);
- 状态向量更新: c t = g i c t ~ + g f c t ? 1 \boldsymbol{c_t = g_i\tilde{c_t} + g_fc_{t-1}} ct?=gi?ct?~?+gf?ct?1?;
- 输出门: g o = σ ( W o [ h t ? 1 ; x t ] + b o ) \boldsymbol{g_o= \sigma(W_o[h_{t - 1};x_t]+b_o)} go?=σ(Wo?[ht?1?;xt?]+bo?);
- 输出向量更新: h t = g o ? t a n h ( c t ) \boldsymbol{h_t = g_o\cdot tanh(c_t)} ht?=go??tanh(ct?)。
总的来说,可以总结三个门的输出值都是 [ 0 , 1 ] \boldsymbol{[0,1]} [0,1] 之间,都是为了控制不同量的"多少"进入下一个 Cell。LSTM 有效地克服了传统 RNN 的一 些不足,比较好地解决了梯度消失、长期依赖等问题。不过,LSTM 也有一 些不足,如结构比较复杂、计算复杂度较高等问题。能否继续改进?
3 GRU
??针对 LSTM 的缺点,我们尝试简化 LSTM 内部的计算流程,特别是减少门控数量。研究发现,遗忘门是 LSTM 中最重要的门控,甚至发现只有遗忘门的简化版网络在多个基准数据集上面优于标准 LSTM 网络。其中,门控循环网络(Gated Recurrent Unit,简称 GRU)是应用最广泛的 RNN 变种之一,GRU 对 LSTM 做了很多简化,比 LSTM 少一个 Gate,因此,计算效率更高,占用内存也相对较少(这也是一件非常有意思的事情,GRU 比 LSTM 提出的更晚,却更简单,且效率更高)。在实际使用中,GRU 和 LSTM差异不大,因此,GRU最近变得越来越流行。GRU 对 LSTM 做了两个大改动:
- 将内部状态向量与输出合并为一个状态: h t \boldsymbol{h_t} ht?;
- 将输入门、遗忘门、输出门变为两个门:更新门(Update Gate)和重置门(Reset Gate)。

3.1 复位门
??复位门用于控制上一个时间戳的状态 h t ? 1 \boldsymbol{h_{t - 1}} ht?1? 进入 GRU 的量。

门控向量
g
r
\boldsymbol{g_r}
gr? 由当前时间戳输入
x
t
\boldsymbol{x_t}
xt? 和上一时间戳状态
h
t
?
1
\boldsymbol{h_{t-1}}
ht?1? 变换得到,关系如下:
g
r
=
σ
(
W
r
[
h
t
?
1
;
x
t
]
+
b
r
)
\boldsymbol{g_r = \sigma(W_r[h_{t-1};x_t]+b_r)}
gr?=σ(Wr?[ht?1?;xt?]+br?)
其中
W
r
\boldsymbol{W_r}
Wr? 和
b
r
\boldsymbol{b_r}
br? 为复位门的参数,可由反向传播算法自动优化,
σ
\boldsymbol{\sigma}
σ 为激活函数,一般使用 Sigmoid 函数。门口向量
g
r
\boldsymbol{g_r}
gr? 只控制
h
t
?
1
\boldsymbol{h_{t-1}}
ht?1? ,而不会控制输入
x
t
\boldsymbol{x_t}
xt?,也就是说,输入会全部进入状态向量中:
h
t
~
=
t
a
n
h
(
W
h
[
g
r
h
t
?
1
;
x
t
]
+
b
h
)
\boldsymbol{\tilde{h_t} = tanh(W_h[g_rh_{t-1};x_t]+b_h)}
ht?~?=tanh(Wh?[gr?ht?1?;xt?]+bh?)
当
g
r
=
0
\boldsymbol{g_r = 0}
gr?=0 时,新输入
h
t
~
\boldsymbol{\tilde{h_t}}
ht?~? 全部来自于输入
x
t
\boldsymbol{x_t}
xt?,不接受
h
t
?
1
\boldsymbol{h_{t-1}}
ht?1?,此时相当于复位
h
t
?
1
\boldsymbol{h_{t-1}}
ht?1?。当
g
r
=?
1
\boldsymbol{g_r \not = 1}
gr??=1 时,
h
t
?
1
\boldsymbol{h_{t-1}}
ht?1? 和输入
x
t
\boldsymbol{x_t}
xt? 共同产生新输入
h
t
~
\boldsymbol{\tilde{h_t}}
ht?~?。
3.2 更新门
??更新门用控制上一时间戳状态 h t ? 1 \boldsymbol{h_{t-1}} ht?1? 和新输入 h t ~ \boldsymbol{\tilde{h_t}} ht?~? 对新状态向量 h t \boldsymbol{h_{t}} ht? 的影响程度。

更新门控向量
g
z
\boldsymbol{g_z}
gz? 计算如下:
g
z
=
σ
(
W
z
[
h
t
?
1
;
x
t
]
+
b
z
)
\boldsymbol{g_z = \sigma(W_z[h_{t-1};x_t] + b_z)}
gz?=σ(Wz?[ht?1?;xt?]+bz?)
其中
W
z
\boldsymbol{W_z}
Wz? 和
b
z
\boldsymbol{b_z}
bz? 为更新门的参数,可由反向传播算法自动优化,
σ
\boldsymbol{\sigma}
σ 为激活函数,一般使用 Sigmoid 函数。
g
z
\boldsymbol{g_z}
gz? 用与控制新输入
h
t
~
\boldsymbol{\tilde{h_t}}
ht?~? 信号,
1
?
g
z
\boldsymbol{1 - g_z}
1?gz? 用于控制状态
h
t
?
1
\boldsymbol{h_{t-1}}
ht?1? 信号:
h
t
=
g
z
h
t
~
+
(
1
?
g
z
)
h
t
?
1
\boldsymbol{h_t = g_z\tilde{h_t} + (1-g_z)h_{t-1}}
ht?=gz?ht?~?+(1?gz?)ht?1?
可以看到,
h
t
~
\boldsymbol{\tilde{h_t}}
ht?~? 和
h
t
?
1
\boldsymbol{h_{t-1}}
ht?1? 对
h
t
\boldsymbol{h_{t}}
ht? 的更新量处于相互竞争、此消彼长的状态。当更新门
g
z
=
0
\boldsymbol{g_z = 0}
gz?=0 时,
h
t
\boldsymbol{h_{t}}
ht? 全部来自上一时间戳状态
h
t
?
1
\boldsymbol{h_{t-1}}
ht?1?;当更新门
g
z
=
1
\boldsymbol{g_z =1}
gz?=1 时,
h
t
\boldsymbol{h_{t}}
ht? 全部来自新输入
h
t
~
\boldsymbol{\tilde{h_t}}
ht?~?。
3.3 小结
??GRU 的核心公式总结如下:
- 复位门: g r = σ ( W r [ h t ? 1 ; x t ] + b r ) \boldsymbol{g_r = \sigma(W_r[h_{t-1};x_t]+b_r)} gr?=σ(Wr?[ht?1?;xt?]+br?);
- 输入向量更新: h t ~ = t a n h ( W h [ g r h t ? 1 ; x t ] + b h ) \boldsymbol{\tilde{h_t} = tanh(W_h[g_rh_{t-1};x_t]+b_h)} ht?~?=tanh(Wh?[gr?ht?1?;xt?]+bh?);
- 更新门: g z = σ ( W z [ h t ? 1 ; x t ] + b z ) \boldsymbol{g_z = \sigma(W_z[h_{t-1};x_t] + b_z)} gz?=σ(Wz?[ht?1?;xt?]+bz?);
- 状态向量更新: h t = g z h t ~ + ( 1 ? g z ) h t ? 1 \boldsymbol{h_t = g_z\tilde{h_t} + (1-g_z)h_{t-1}} ht?=gz?ht?~?+(1?gz?)ht?1?。
能够发现,GRU 和 LSTM 的门控制向量的计算方式都一样,只不过 GRU 比 LSTM 更加简洁一些,只要按照 Cell 里面的结构一步一步进行推理,也是不难的。
