[人工智能]OpenCV中的图像直方图（22）

直方图

在进行物体图像和视频信息分析的过程中，我们通常习惯与将看到的物体用直方图表示出来，得到比较直观的图像物体数据。直方图可以用不同的参数和事物来表示如物体的色彩分布,物体的边缘梯度模板,以及表示目标位置的当前假设的概率分布.
1.1 图像直方图
简单的说,直方图就是对数据进行统计的方法,并将统计值放到一系列事先定义好的bin(直条或组距)当中,直方图对应的数值就是从图像数据中计算出的特征统计量,这些特征可以是梯度,方向,色彩或任何其他特征.
我们要讲的直方图是用以表示数学图像中亮度分布的直方图,绘制了图像中每个亮度值的像素数,同时也是图像中像素强度分布的图形化表示.
直方图的介绍中我们用到了bin术语,那我们再讲讲直方图中其他的一些术语:

• dims:需要统计的特征的数目.在直方图中我们统计了图像的强度信息,所以此时的dims=1
• bins:每个特征空间子区段的数目，如0-255个亮度值，可以分为16个bins,每个bins含有15个亮度值。
• range:每个特征空间的取值范围。如亮度特征空间的话取值范围是0～255

1.2 直方图的计算和绘制
直方图的计算在OpenCV中可以使用calHist()函数，计算完成后可以使用OpenCV中的绘图函数，如rectangle()和line()函数来完成。
1.3 计算直方图：calcHist()函数
void calcHist(const Mat* images, int nimages, const imt* channels, InputArray mask, OutputArray hist, int dims, const int*histSize, const float** ranges, bool uniform= true, bool accumulate=false)

• 参数一：const Mat* images输入数组，需要具有相同的深度和相同的尺寸。
• 参数二：nimages 输入数组的个数，也就是第一个参数中有多少张图像，由几个原数组组成。
• 参数三：channels,需要统计的通道（dim)索引。第一个数组通道从0到image[0].channels()-1, 第二个数组通道从images[0]. channel()计算到images[0].channels()+images[1].channels()-1。
• 参数四：mask 可选的操作掩码。如果此掩码不为空，必须为8位，并且与image[i]有同样的大小的尺寸。这里的非零掩码元素用于标记出直方图的数组元素数据。
• 参数五：hist，输出的目标直方图，一个二维数组。
• 参数六：dims，需要计算的直方图的维度，必须是正数，且小与CV_MAX_DIMS（32）
• 参数七：histSize, 存放每个维度的直方图尺寸的数组。
• 参数八：ranges,表示第六个参数的每一维数组的边界阵列，就是每一维数值的取值范围。
• 参数九：uniform,直方图是否均匀的标志符，默认true.
• 参数十：accumulate,累积标志符，默认false,如果为true表示直方图在配置阶段不会被清零。主要是用来从多个直方图中计算单个直方图，或者用于在特定的时间更新直方图。

1.4 寻找最值：minMaxLoc()函数
minMaxLoc()函数的作用是在数组中找到全局最大和最小值。
函数原型：void minMaxLoc(InputArray src, double* minVal, double* maxVal =0, Point* minLoc=0, Point* maxLoc=0, InputArray mask = noArray())

• 参数一：src，输入的单通道阵列
• 参数二：返回最小值的指针，若无返回，填NULL
• 参数三：返回最大值的指针
• 参数四：返回最小位置的指针(二维情况下)。若无需返回，填NULL
• 参数五：返回最大位置的指针(二维情况下)。
• 参数六：mask,用于选择子阵列的可选掩膜

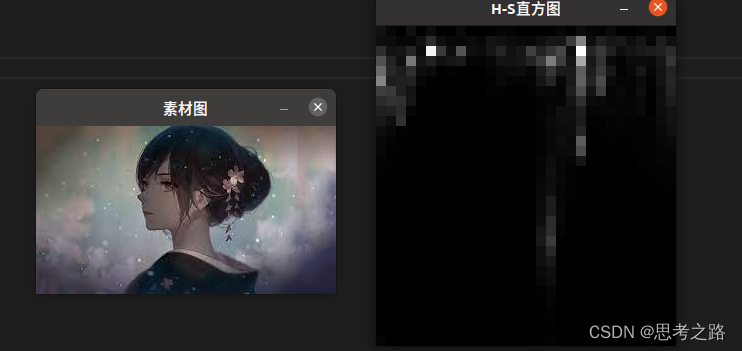
1.5 示例H-S直方图
计算彩色图像的色调(Hue)，饱和度(Saturation)二维直方图
实现代码：

#include "opencv2/opencv.hpp"
#include "opencv2/imgproc/imgproc.hpp"
using namespace cv;

int main()
{
    Mat srcImage, hsvImage;
    srcImage = imread("../1.jpg");
    cvtColor(srcImage, hsvImage, COLOR_BGR2HSV);

    //准备参数
    //将色调量化为30个等级，饱和度量化为32个等级
    int hueBinNum = 30; //色调的直方图直条数
    int saturationBinNum = 32; //饱和度的直方条的组距数

    int histSize[] = {hueBinNum, saturationBinNum};

    //色调的范围0-179
    float hueRanges[] = {0, 180};
    float saturationRanges[] = {0, 256};
    const float* ranges[] = {hueRanges, saturationRanges};

    MatND dstHist;//MatND类是用于存储直方图的一种数据结构
    //calHist将计算0，1通道的直方图
    int channels[] = {0, 1};

    calcHist(&hsvImage, 1, channels, Mat(), dstHist, 2, histSize, ranges, true, false);
    
    //绘制直方图准备参数
    double maxValue = 0; // 最大值
    minMaxLoc(dstHist, 0 ,&maxValue, 0, 0);
    int scale = 10;
    Mat histImage = Mat::zeros(saturationBinNum * scale, hueBinNum * 10, CV_8UC3);

    //双层循环进行直方图的绘制
    for(int hue=0; hue < hueBinNum; hue++)  //行代表色调，列代表饱和度
    {
        for(int saturation = 0; saturation < saturationBinNum; saturation++)
        {
            float binValue = dstHist.at<float>(hue, saturation);  //直方图值条的值
            int intensity = cvRound(binValue * 255/maxValue);  //强度

            //绘制
            rectangle(histImage, Point(hue * scale, saturation * scale), Point((hue + 1) * scale - 1, (saturation+1) * scale - 1), Scalar::all(intensity), FILLED);
        }
    }
    imshow("素材图", srcImage);
    imshow("H-S直方图", histImage);
    // waitKey();
    while (char (waitKey(1)) != 'q')
    {
        /* code */
    }
    
}

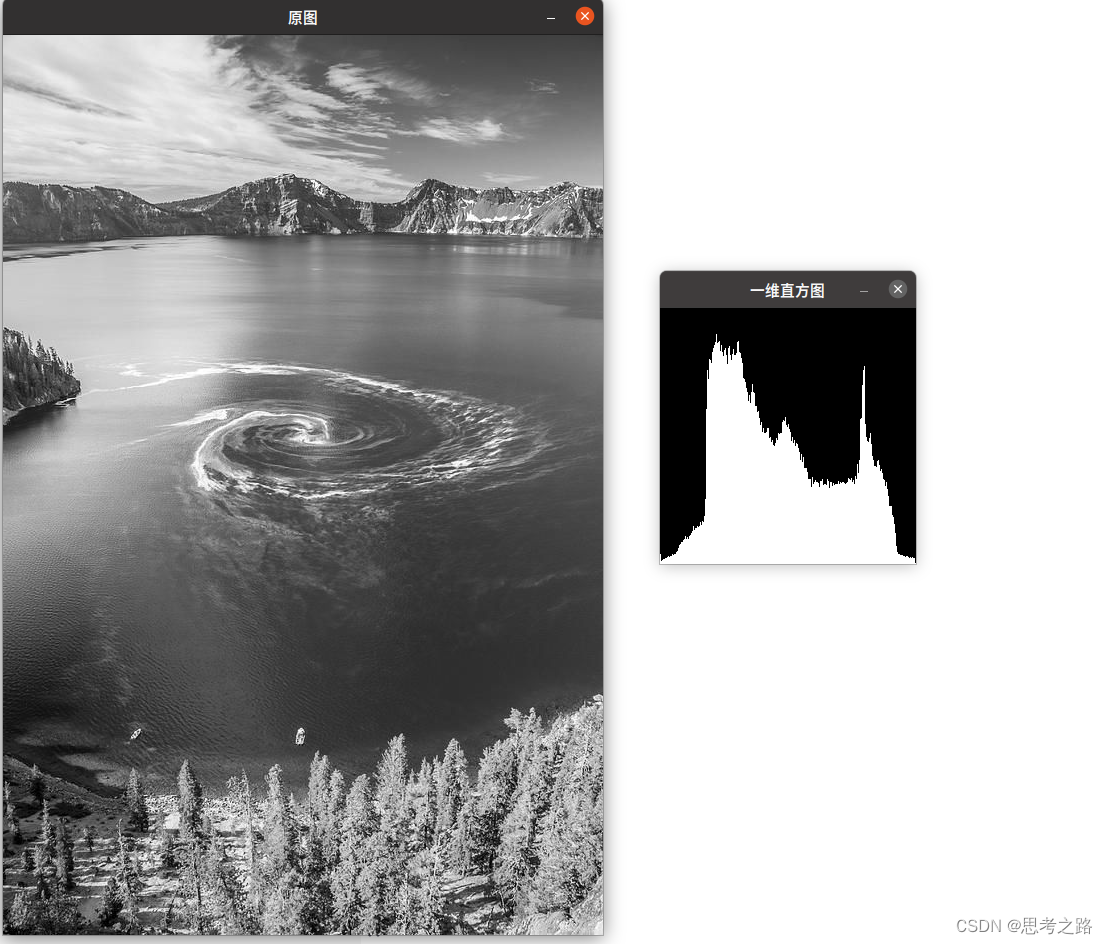
以上示例是H-S二维直方图，接下俩我们来绘制一维的直方图。
示例：绘制一维直方图

#include "opencv2/opencv.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
using namespace std;
using namespace cv;

int main()
{
    Mat srcImage = imread("../1.jpg", 0);
    imshow("原图", srcImage);

    if(!srcImage.data)
    {
        cout << "fail to load image"  << endl;
        return 0;
    }

    MatND dstHist;
    int dims =1;
    float hranges[] = {0, 255};
    const float* ranges[] = {hranges};
    int size = 256;
    int channels = 0;

    calcHist(&srcImage, 1, &channels, Mat(), dstHist, dims, &size, ranges);
    int scale = 1;

    Mat dstImage(size * scale, size, CV_8U, Scalar(0));
    double minValue =0;
    double maxValue = 0;
    minMaxLoc(dstHist, &minValue, &maxValue, 0, 0);

    int hpt = saturate_cast<int>(0.9 * size);  //可以看成是类型的强制转换，比如对于saturate_cast<uchar>来说，就是把数据转换成8bit的0~255区间，负值变成0，大于255的变成255。如果是浮点型的数据，变成round最近的整数
    for(int i = 0; i < 256; i++)  //像素左上角是(0,0)点
    {
        float binValue = dstHist.at<float>(i);
        int realValue = saturate_cast<int>(binValue * hpt/maxValue);
        rectangle(dstImage, Point(i*scale, size -1), Point((i+1)*scale - 1, size - realValue), Scalar(255));
    }
    imshow("一维直方图", dstImage);
    // waitKey(0);
    while(char (waitKey(1)) != 'q'){}
    return 0;
}

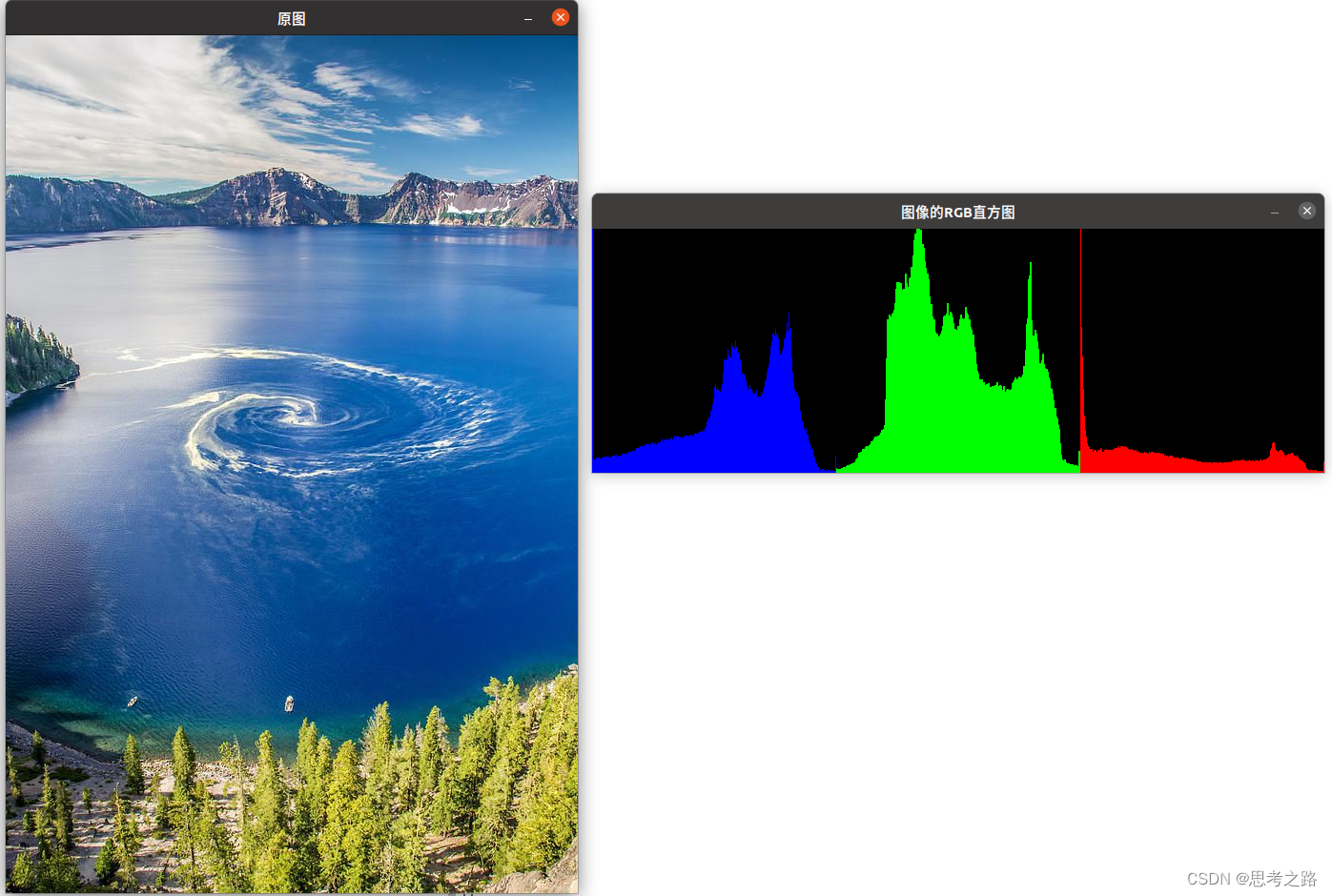
示例：绘制RGB三色直方图

#include "opencv2/opencv.hpp"
#include "opencv2/imgproc/imgproc.hpp"
using namespace cv;

int main()
{
    Mat srcImage = imread("../1.jpg");
    imshow("原图", srcImage);

    int bins = 256;
    int hist_size[] = {bins};
    float range[] = {0, 256};
    const float* ranges[] = {range};
    MatND redHist, grayHist, blueHist;
    int channels_r[] = {0};

    calcHist(&srcImage, 1, channels_r, Mat(), redHist, 1, hist_size, ranges, true, false);

    int channels_g[] = {1};
    calcHist(&srcImage, 1, channels_g, Mat(), grayHist, 1, hist_size, ranges, true, false);

    int channels_b[] = {2};
    calcHist(&srcImage, 1, channels_b, Mat(), blueHist, 1, hist_size, ranges, true, false);

    double maxValue_red , maxValue_green, maxValue_blue;
    minMaxLoc(redHist, 0, &maxValue_red, 0, 0);
    minMaxLoc(grayHist,0, &maxValue_green, 0, 0);
    minMaxLoc(blueHist, 0, &maxValue_blue, 0 , 0);
    int scale = 1;
    int histHeight = 256;
    Mat histImage = Mat::zeros(histHeight, bins*3, CV_8UC3);

    for(int i = 0; i < bins; i++)
    {
        float binValue_red = redHist.at<float>(i);
        float binValue_gray = grayHist.at<float>(i);
        float binValue_blue = blueHist.at<float>(i);

        int intensity_red = cvRound(binValue_red * histHeight / maxValue_red); //要绘制的高度
        int intensity_gray = cvRound(binValue_gray * histHeight/ maxValue_green); 
        int intensity_blue = cvRound(binValue_blue * histHeight / maxValue_blue);

        //绘制红色分量的直方图
        rectangle(histImage,Point(i * scale, histHeight - 1), Point((i+1) * scale - 1, histHeight - intensity_red), Scalar(255, 0, 0));
        rectangle(histImage,Point((i + bins) * scale, histHeight -1), Point((i + bins) * scale - 1, histHeight - intensity_gray), Scalar(0, 255, 0));
        rectangle(histImage,Point((i + bins * 2) * scale, histHeight - 1), Point((i + bins * 2 + 1) * scale - 1, histHeight - intensity_blue), Scalar(0, 0, 255));
        
    }

    imshow("图像的RGB直方图", histImage);
    // waitKey(0);
    while(char(waitKey(1)) != 'q'){}
    return 0;
    
}

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖