摘要
在分类问题中,常使用Cross-entropy loss和Focal loss。通过泰勒展开来逼近函数,作者提出了一个简单的框架,称为PolyLoss,将损失函数设计为多项式函数的线性组合。PolyLoss可以让Polynomial bases(多项式基)根据目标任务和数据集进行调整,同时也可以将上述Cross-entropy loss和Focal loss作为PolyLoss的特殊情况。PolyLoss在二维图像分类、实例分割、目标检测和三维目标检测任务上都明显优于Cross-entropy loss和Focal loss。
主要贡献
本文主要是提出了一个新的框架来理解和设计损失函数。
思路为常用的分类损失函数,如Cross-entropy loss和Focal loss,分解为一系列加权多项式基,多项式系数为标类标签的预测概率。每个多项式基由相应的多项式系数进行加权。
Cross-entropy loss和Focal loss是PolyLoss的两种常用情况。
在不同的任务和数据集需要调整多项式系数,只需调整单多项式系数,即可实现比Cross-entropy loss和Focal loss的更好的性能。
公式
Cross-entropy loss和Focal loss的泰勒展开式如下,式中为模型对目标类的预测概率。
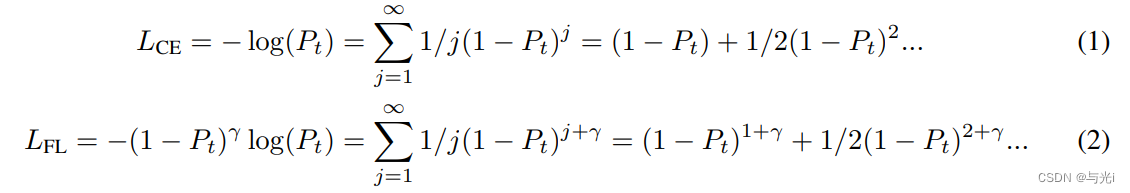
在PolyLoss框架中,使用梯度下降法来优化交叉熵损失需要对Pt进行梯度求导,系数
1
/
j
1/j
1/j可与指数
j
j
j抵消。
可得公式3。
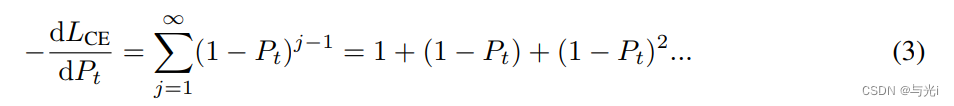
因此Cross-entropy loss的梯度变成了多项式的和。
在PolyLoss框架中,Focal loss通过调制因子γ简单地将移动。这相当于水平移动所有的多项式系数的γ。
Focal loss梯度如下。
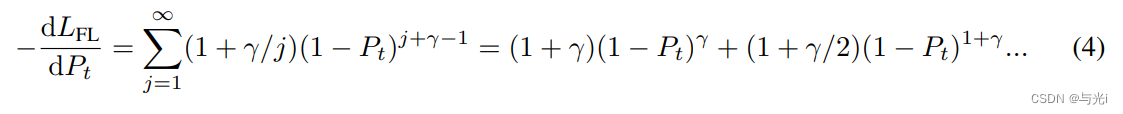
对于正的γ,Focal loss的梯度降低了Cross-entropy loss中恒定的梯度项1。
通过将所有多项式项的幂移动γ,第1项就变成
(
1
?
P
t
)
γ
(1-P_t)^γ
(1?Pt?)γ,被γ抑制,以避免过拟合到(即接近1)多数类。
一般来说,PolyLoss是[0,1]上的单调递减函数,可以表示为
∑
j
=
1
∞
α
i
(
1
?
P
t
)
j
\sum^\infty_{j=1}\alpha_i(1-P_t)^j
∑j=1∞?αi?(1?Pt?)j,
并提供了一个灵活的框架来调整每个系数。
PolyLoss可以推广到非整数j,但为简单起见,只关注整数幂。
多项式系数的影响
探索了3种分配多项式系数的不同策略:
- 去掉高阶项
- 调整多个靠前多项式系数
- 调整第1个多项式系数
结果如图1。

图1
作者发现,调整第1个多项式系数(Poly-1)便可以最大的增益,而且仅仅需要很小的代码更改和超参数调整。
高阶多项式项的删除
已有研究表明,降低高阶多项式和调整前置多项式可以提高模型的鲁棒性和性能。作者采用相同的损失公式,并在ImageNet-1K上比较它们与基线Cross-entropy loss的性能。
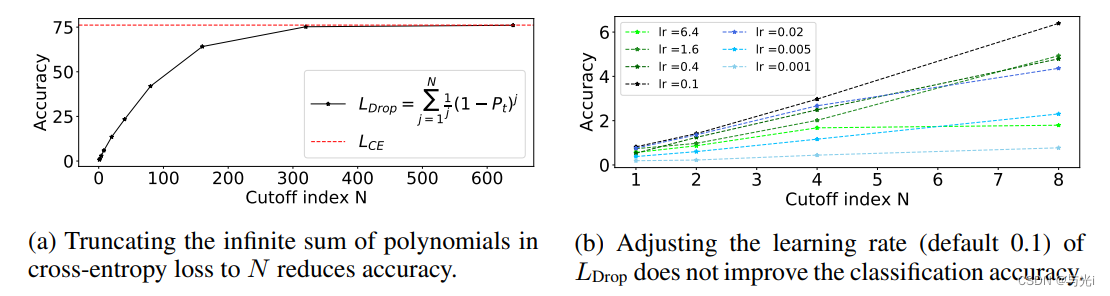
图2
图2a所示,需要求和超过600个多项式项才能匹配Cross-entropy loss的精度。值得注意的是,去除高阶多项式不能简单地解释为调整学习率。为了验证这一点,图2b比较了在不同的截止条件下不同学习率下的性能:无论从初始值0.1增加或减少学习率,准确率都会变差。
在PolyLoss框架中,丢弃高阶多项式等价于将所有高阶(j>N+1)多项式系数垂直推到0。
扰动重要的多项式系数
一般来说,有无穷多个多项式系数需要调节。因此,对最一般损失进行优化是不可行的。
如果将方程中的无限和截断到前几百项,那么对这么多多项式的调优系数会带来一个非常大的搜索空间。此外,综合调整许多系数也不会优于Cross-entropy loss。
为了解决这一问题,作者提出扰动交叉熵损失中的重要的多项式系数(前N项),同时保持其余部分不变。将所提出的损失公式表示为,其中N表示将被调整的重要系数(前N项)的数量。
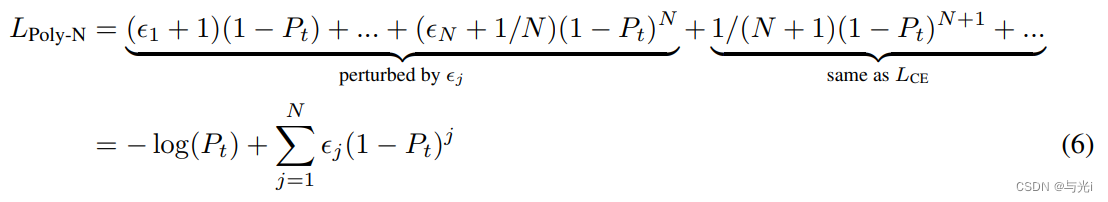
这里用
1
/
j
+
ε
j
1/j+\varepsilon_j
1/j+εj?替代
1
/
j
1/j
1/j,
ε
j
∈
[
?
1
/
j
,
∞
]
\varepsilon_j\in[-1/j,\infty]
εj?∈[?1/j,∞]是扰动项。
这使得可以精确地定位第1个N个多项式,而不需要担心无限多个高阶(j>N+1)系数。
图3表示PolyLoss性能优于Cross-entropy loss。
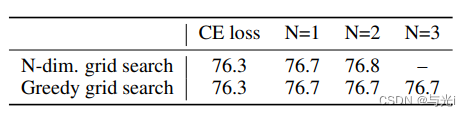
图3
简化
作者发现调整第1个多项式项会带来最显著的增益。在本节中,进一步简化了Poly-N公式,并重点计算了Poly-1,其中只修改了Cross-entropy loss中的第1个多项式系数。
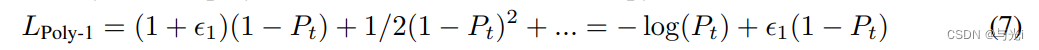
作者还研究了不同第1项缩放对精度的影响,并观察到增加第1个多项式系数可以提高ResNet-50的精度,如图4a所示。
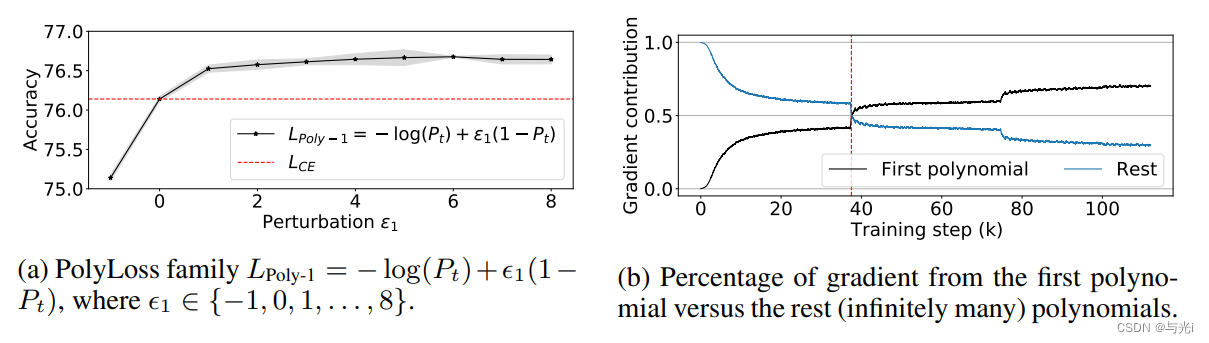
图4
实验
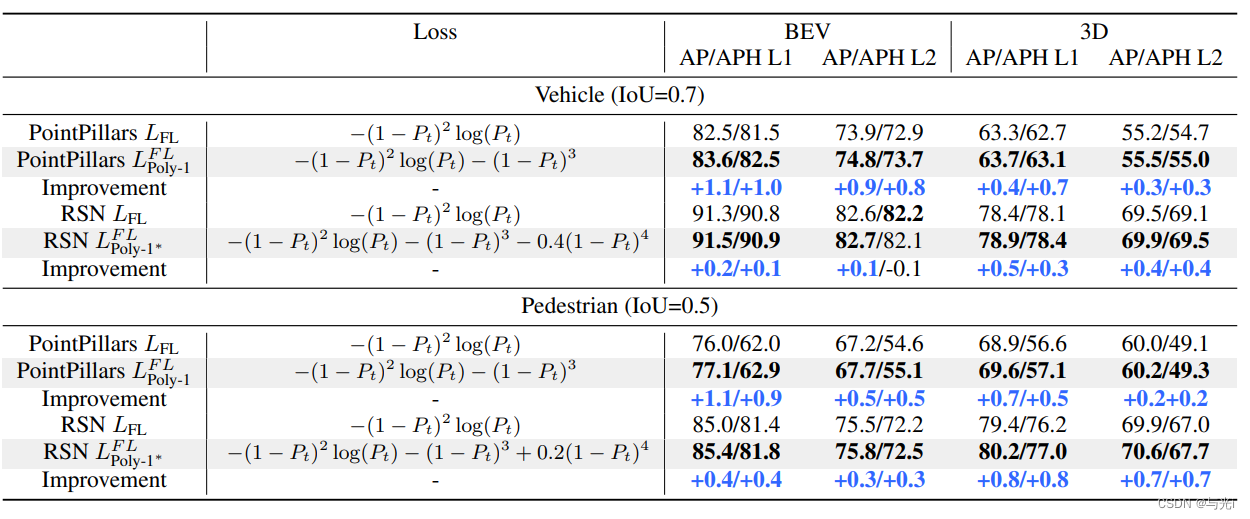
图像分类上。
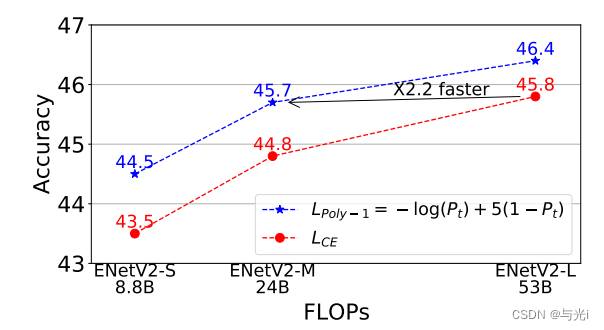
目标检测上。

3D目标检测上。