[人工智能]相干采样 FFT python

import numpy
import numpy as np
from scipy.fftpack import fft
import matplotlib.pyplot as plt
from matplotlib.pylab import mpl

mpl.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
mpl.rcParams['axes.unicode_minus'] = False  # 显示负号

# https://drr.ikcest.org/app/s0019
# fDSAMPLE: 2000, fDIN:68, nRECORD, 1024, SIGFIG: 4

# 采样点选择1400个，因为设置的信号频率分量最高为600赫兹，根据采样定理知采样频率要大于信号频率2倍，
# 所以这里设置采样频率为1400赫兹（即一秒内有1400个采样点）
N = 10000  # 设置1400个采样点
Samples = 1024
Fsignal = 68.25
Fsample = 1996.8
x = [round(2 * np.pi * Fsignal * a * 1 / Fsample, 2) for a in range(N)]
print(x)

# y = 1 * np.sin(2 * np.pi * 68.3585 * x[0:1024])
y = 1 * np.sin(x[0:Samples])

# plt.magnitude_spectrum(y, Fs=1999.9744, scale='dB')


fft_y = fft(y)  # 使用快速傅里叶变换，得到的fft_y是长度为N的复数数组

x = np.arange(Samples)  # 频率个数（x的取值涉及到横轴的设置，这里暂时忽略，在第二节求频率时讲解）

abs_y = np.abs(fft_y)  # 取复数的绝对值，即复数的模
print(abs_y)

normalization_y = abs_y / (Samples / 2)  # 归一化处理（双边频谱）
normalization_y[0] /= 2

xxx = 20. * np.log10(normalization_y)
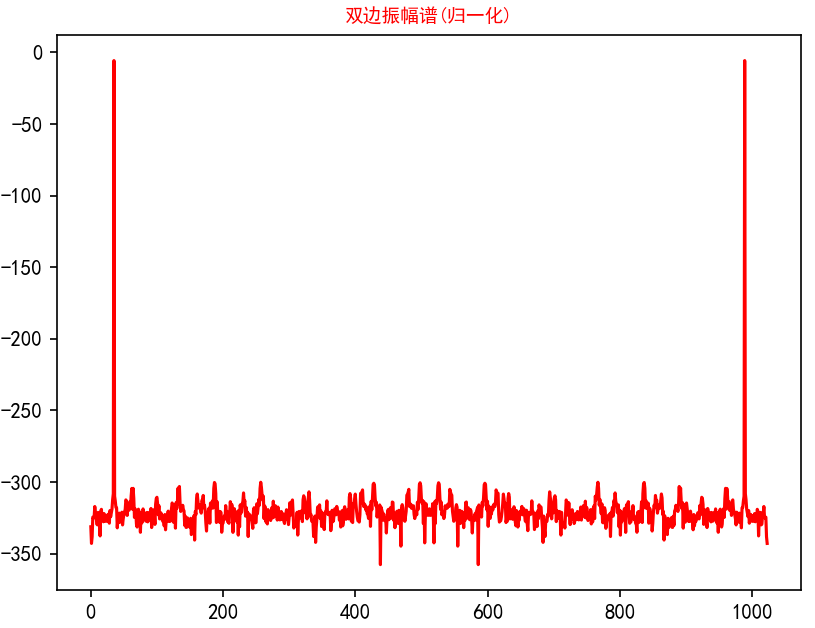
plt.plot(x, xxx, 'r')

# plt.plot(x, normalization_y, 'r')
plt.title('双边振幅谱(归一化)', fontsize=9, color='red')
plt.show()

Coherent Sampling Calculator_Online Calculation Tool,Online computing, online calculator, calculator online calculationhttps://drr.ikcest.org/app/s0019?

?显示前面40个数据：第35个数据为1.0

[0.0, 0.0, 0.0, 0.0, 0.0001, 0.0001, 0.0, 0.0, 0.0, 0.0, 0.0001, 0.0001, 0.0001, 0.0001, 0.0003, 0.0007, 0.0002, 0.0001, 0.0001, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0001, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0]

35是怎么来的呢？

Samples = 1024
Fsignal = 68.25
Fsample = 1996.8

68.25/(1996.8/1024)=35

1996.8/1024表示频率分辨率，采样频率除以采样点数。

68.25/1996.8=35/1024(fSignal/fSample=M/N(M,N必须互质))。

相干采样要求采样整数个信号周期。这样信号频率就会落在频域的整数点上，不会存在频率泄漏。

信号频率除以频率分辨率，即可得到信号频率在频域的索引。

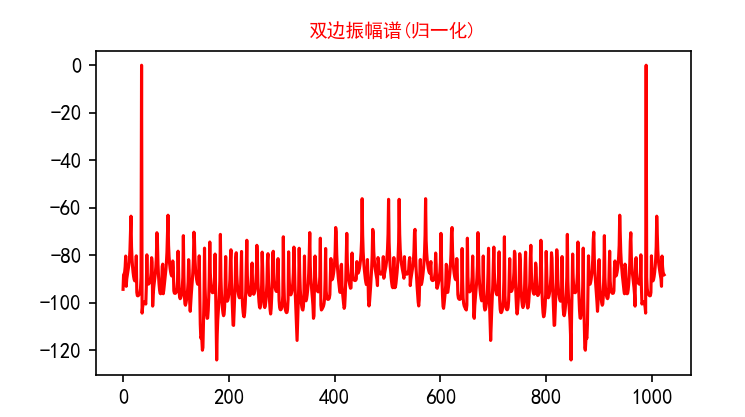
如果将68.25更改为68，即得到下面的幅频图。可见存在明显的频谱泄漏。

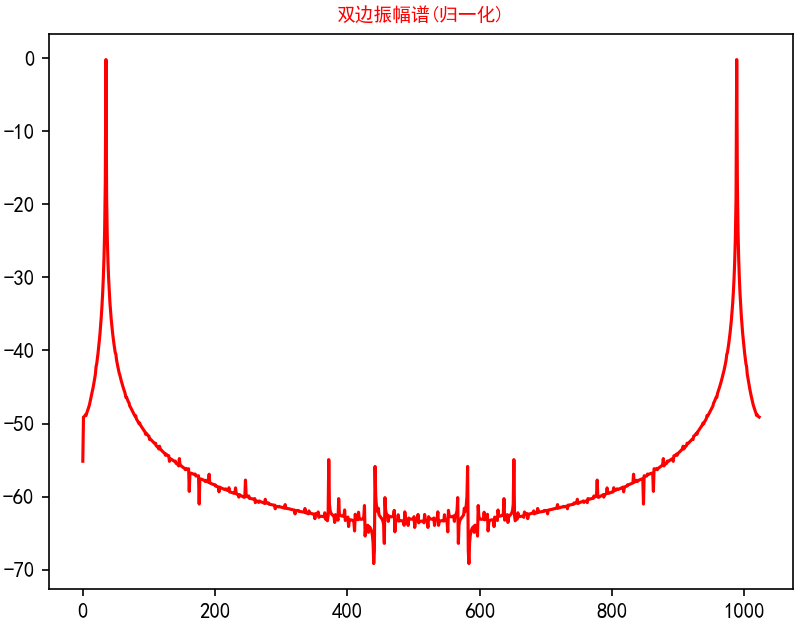
?SIGFIG的位数对SNR的影响很大，位数越大，说明LSB的分辨率越大，6.02n+1.76，说明n越大。下面的处理就是进行精度控制。在没有添加这个函数时，SNR都可以到-300dB，明显不合情理。

round(2 * np.pi * Fsignal * a * 1 / Fsample, 2)

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖