- 概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。
- 统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。
- sdt 标准偏差(Std Dev,Standard Deviation) -统计学名词，标准差是方差的算术平方根。一种度量数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。
统计函数
-
原文： [支持的统计函数](https://blog.csdn.net/weixin_41715077/article/details/103747504#:~:text=%23%20sdt%20%E6%A0%87%E5%87%86%E5%81%8F%E5%B7%AE(Std%20Dev,%E8%B6%8A%E5%B0%91%EF%BC%8C%E5%8F%8D%E4%B9%8B%E4%BA%A6%E7%84%B6%E3%80%82)
-
其中大部分函数是使用的Base 或者Statistics的内置函数#(
sum,prod,minimum,maximum,mean,var,std,first,lastandlength) -
，只有其中的sdt函数是在DataFrame中定义的。
可以按照列名(可以是多列)分组， 对其他列（Vector）做计算，可以计算多列，可以计算的时候重命名列
mean 平均值 ，
var 计算基于给定样本的方差，概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。
样本方差计算公式：
S^2= ∑（X-） ^2 / （n-1） [2] ，S^2为样本方差，X为变量，为样本均值，n为样本例数。
sdt 标准偏差(Std Dev,Standard Deviation) -统计学名词，标准差是方差的算术平方根。一种度量数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量，样本标准偏差计算公式：
，代表所采用的样本X1,X2,…,Xn的均值。
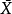代表所采用的样本X1,X2,…,Xn的均值。
minimum :列中最小
maximum :列中最大
median: 函数是一种计算机函数，能够返回给定数值的中值，中值是在一组数值中居于中间的数值，如果参数集合中包含偶数个数字，函数 MEDIAN 将返回位于中间的两个数的平均值。
eltype :列中每个值的类型
first :列中第一个值
last :列中最后个值
sum :求和
prod :prod函数用于求一列元素的乘积，可用于求积。
length :列的长度
标准差和标准误差、平均值
- 原文： 标准差和标准误差、平均值
SS用于表示离均差的平方和
对于总体，方差为：SS/N
对于样本，方差为：SS/(n-1)，以此成为对总体的无偏估计
标准差均为：sqrt（方差）
标准误差：sqrt（SS/n/(n-1)），也就是说，对于样本，excel需要用STDEV.S计算无偏估计作为方差，或者直接用SPSS描述，标准误差再次基础上需要除以：sqrt(n)
