[人工智能]机器学习问题汇总（分类篇）

本篇博文主要介绍机器学习里面常遇到的一些分类相关问题。

1. 监督学习和无监督学习的区别

监督学习的训练数据拥有标记信息，无监督学习的没有标记信息，分类和回归是监督学习的代表，聚类是无监督学习的代表。

2. 如果数据有问题，怎么处理

第一种情况是数据存在缺失值，对缺失值的处理方法有：删除、统一值填充、统计值填充、前后向值填充、插值法填充、建模预测填充和具体分析几种方法。
第二种情况是数据存在异常值，可以删除或者修正填补。

3. 相对熵公式

用于衡量同一个随机变量$X$的两个分布$p(x)$和$q(x)$之间的差异，$p(x)$常用于描述样本的真实分布，$q(x)$用于表示预测的分布。

$D_{KL}p||q)={\sum }_{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)})$

KL散度的值越小表示两个分布越接近。

4. 交叉熵公式

把KL散度的公式变形，得到：

$$\begin{gathered} D_{KL}p||q)={\sum }_{i=1}^{n}p(x_i)log(p(x_i))?{\sum }_{i=1}^{n}p(x_i)log(q(x_i)) \\ =?H(p(x))+[?{\sum }_{i=1}^{n}p(x_i)log(q(x_i))] \end{gathered}$$

前半部分是$p(x)$的熵，后半部分是交叉熵

$H(p,q)=?{\sum }_{i=1}^{n}p(x_i)log(q(x_i))$

5. LR的推导，损失函数

$sigmoid$函数：

$\sigma (x)=\frac{1}{1+e^{?x}}$

其图像如下：

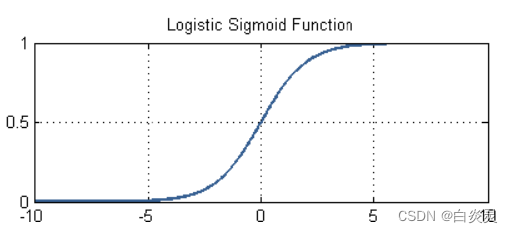
把线性回归的输出作为$sigmoid$函数的输入：

$\sigma (f(x))=\frac{1}{1+e^{?w^T}x}$

损失函数是衡量真实输出和模型输出的差别。
$$\begin{gathered} P=P(y_1|x_1)P(y_2|x_2)...P(y_N|x_N) \\ ={\prod }_{n=1}^N{p}^{y_n}(1?p{)}^{1?y_n} \end{gathered}$$

通过两边取对数把连乘变为连加的形式，即：
$F(w)=ln(P)={\sum }_{n=1}^N(y_{n}ln(p)+(1?y_n)ln(1?p))$

这里损失函数的值等于事件发生的总概率，希望它越大越好，按照习惯吧，都是最小化损失函数，可以在$F(w)$前面加个负号。

6. LR和线性回归的区别与联系

都是广义上的线性回归。
线性回归的优化方法是最小二乘法，而LR是似然函数。
线性回归主要是解决回归问题，LR主要是解决分类问题。
线性回归的输出是实数域上的连续值，LR的输出被sigmoid函数映射到(0,1)之间，通过设置阈值转换为分类类别。

7. 逻辑回归怎么实现多分类

方法一：
把多分类任务拆解成多个二分类任务，利用逻辑回归分类器进行投票求解。有三种拆分策略，OvO、OvR、MvM逻辑回归实现多分类

OvO：转化为多个二分类
OvR：一对其余，一个类别作为正例，其余所有类别作为反例
MvM：将若干个类作为正例，若干个其他类作为反例

方法二：
对传统的逻辑回归模型改造

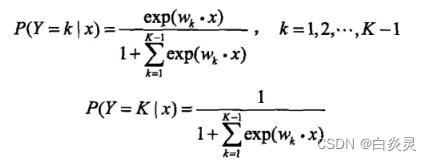
8. 什么是支持向量机

支持向量机SVM就是一种二类分类模型，基本模型是定义在特征空间上的间隔最大的线性分类器，其学习策略就是间隔最大化。
间隔的定义：

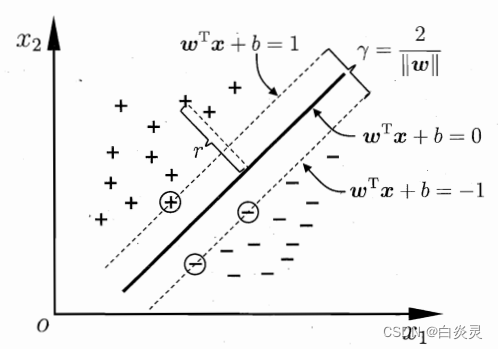
支持向量机的基本型：

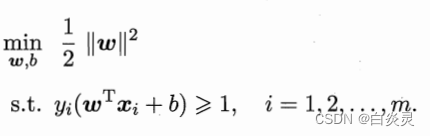
9. SVM的硬间隔，软间隔表达式

硬间隔表达式：

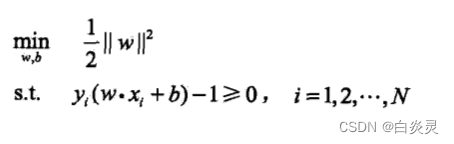
当训练数据中有一些特异点，不能满足函数间隔大于等于1的约束条件，引入松弛变量${\xi }_i\ge 0$，约束条件变为：$y_i(w_i?x_i+b)\ge 1?{\xi }_i$，同时，对每个松弛变量${\xi }_i$，支付一个代价${\xi }_i$，目标函数变为下面的，这里的$C>0$称为惩罚参数，一般由应用问题决定，$C$值越大时对误分类的惩罚增大，$C$值越小时对误分类的惩罚减小。
软间隔表达式：

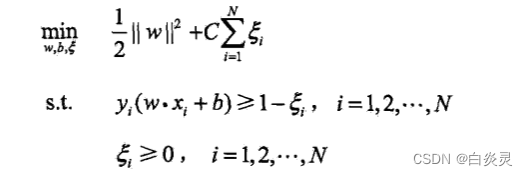
10. SVM使用对偶计算的目的是什么，如何推出来的，手写推导；

9中的SVM基本型是一个凸二次规划问题，可以利用现成的优化计算包求解，但引入对偶问题更容易求解。“引入核函数，进而推广到非线性分类问题。”

对9中的每条约束添加拉格朗日乘子${\alpha }_i>=0$，该问题的拉格朗日函数可写为：
$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+{\sum }_{i=1}^m{\alpha }_i(1?y_i(w^T{x}_i+b))$

令${\theta }_i=ma{x}_{{\alpha }_i\ge 0}L(w,b,\alpha )$，现在目标就是最小化${\theta }_i$

分别求$L(w,b,\alpha )$对$w$和$b$的偏导：
$\frac{?L}{?w}=w?{\sum }_{i=1}^m{\alpha }_i{y}_i$
$\frac{?L}{?b}=?{\sum }_{i=1}^m{\alpha }_i{y}_i$
令偏导都等于0可得：
$w={\sum }_{i=1}^m{\alpha }_i{y}_i$
${\sum }_{i=1}^m{\alpha }_i{y}_i=0$

最后代入拉格朗日函数可得：
$L(w,b,\alpha )=?\frac{1}{2}{\sum }_i^m{\sum }_j^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j+{\sum }_{i=1}^m{\alpha }_i$

所以对偶问题为：
$max\frac{1}{2}{\sum }_i^m{\sum }_j^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j?{\sum }_{i=1}^m{\alpha }_i$

11. SVM的物理意义是什么

构造一个最优化的超平面，以充分大的确信度对训练数据进行分类，希望对于离超平面最近的点也有足够大的确信度将它们分开。

12. SVM的损失函数

采用hinge损失时，损失函数为：

$\frac{1}{2}||w|{|}^2+C{\sum }_{i=1}^{m}max(0,1?y_i(w^T{x}_i+b))$

指数损失：$l_{exp}(z)=exp(?z)$
对率损失：$l_{log}(z)=log(1+exp(?z))$

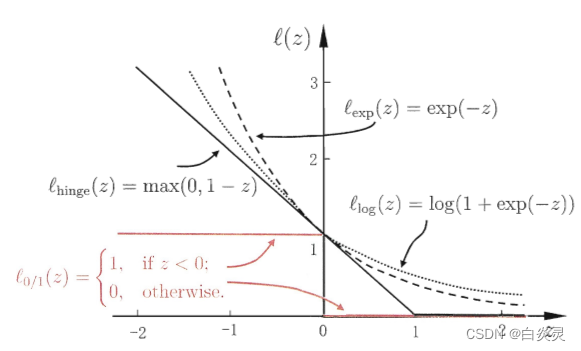
13. SVM核函数的作用、种类

核函数的作用就是把样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。如果原始空间是有限维的，即属性数有限，那么一定存在一个高维特征空间使样本可分。

14. SVM中什么时候用线性核什么时候用高斯核?

线性核：主要用于线性可分、特征维数高的情形，参数少，速度快，对于一般数据，分类效果已经很理想。
高斯核：主要用于线性不可分、特征维数比较少的情形，参数多，分类结果非常依赖于参数。

15. 为什么高斯核能够拟合无穷维度

高斯核函数：

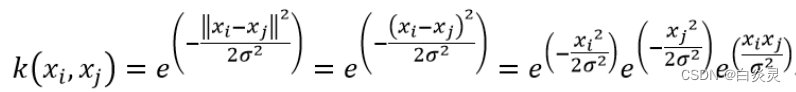
根据泰勒展开式：
$e^x={\sum }_{n=0}^{\infty }\frac{x^n}{n!}$

代入上式第三项得：

映射函数为：
$?(x)=\sqrt{\frac{1}{n!{\sigma }^{2n}}}exp(?\frac{x^2}{2{\sigma }^2})x^n$

即高斯核函数将输入空间映射到了无穷多维空间。

16. SVM和全部数据有关还是和局部数据有关

SVM只和分类界限上的支持向量点有关,换而言之只和局部数据有关。

17. LR和SVM 的区别与联系

都是有监督的分类算法。
LR是参数模型，SVM是非参数模型。
SVM不直接依赖数据分布，LR依赖。
LR的损失函数是交叉熵，而SVM是hinge函数。

18. 机器学习中的距离计算方法

欧式距离：
$d(x,y)=\sqrt{{\sum }_{k=1}^n(x_k?y_k{)}^2}$
$n$是维数，而$x_k$和$y_k$分别是$x$和$y$的第$k$个属性

闵可夫斯基距离：（欧式距离的推广）
$d(x,y)={({\sum }_{k=1}^n|x_k?y_k{|}^r)}^{1/r}$

$r=1$时，称为街区距离（或曼哈顿距离，$L_1$范数）
$r=2$时，就是前面介绍的欧式距离（或$L_2$范数）
$r\to \infty$时，称为切比雪夫距离（或$L_{max}$范数）
$$\begin{gathered} d(x,y)=li{m}_{r\to \infty }{({\sum }_{k=1}^n|x_k?y_k{|}^r)}^{1/r} \\ =ma{x}_k(|x_k?y_k|) \end{gathered}$$

杰卡德相似系数(Jaccard)：
$J(A,B)=\frac{|A\cap B|}{|A\cup B|}$

余弦相似度(cosine similarity)：
$cos(\theta )=\frac{a^{T}b}{|a|?|b|}$

Pearson相似系数（是对象之间线性联系的度量）：
$$\begin{gathered} {\rho }_{XY}=\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y} \\ =\frac{E[(X?{\mu }_X)(Y?u_Y)]}{{\sigma }_X{\sigma }_Y} \end{gathered}$$

相对熵（K-L距离）：
$$\begin{gathered} D(p||q)={\sum }_{x}p(x)log\frac{p(x)}{q(x)} \\ =E_{p(x)}log\frac{p(x)}{q(x)} \end{gathered}$$

Hellinger距离：

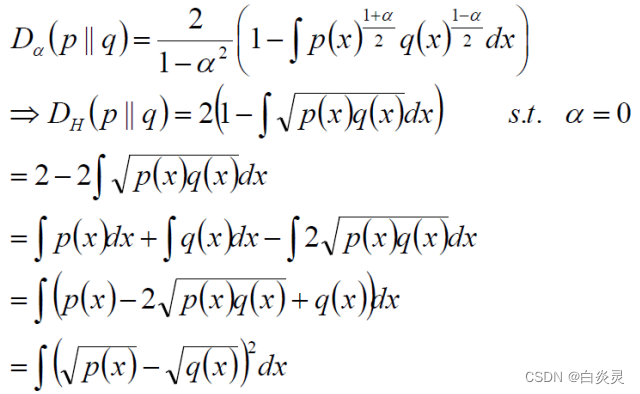
19. 训练集中类别不均衡，哪个评价指标最不准确

在数据不均衡时，准确度accuracy这个评价指标最不标准，参考意义不大。

20. ID3、C4.5和CART三种决策树的区别

ID3算法：信息增益

C4.5算法：信息增益率
特征A对训练数据集D的信息增益比$g_R(D,A)$定义为其信息增益$g(D,A)$与训练数据集D的经验熵$H(A)$之比：
$g_R(D,A)=\frac{g(D,A)}{H(A)}$

CART算法：基尼指数
分类问题中，假设有$K$个类，样本点属于第$K$类的概率为$p_k$，则概率分布的基尼指数定义为：
$Gini(p)={\sum }_{k=1}^K{p}_k(1?p_k)$

对于二类分类问题，若样本点属于第1个类的概率是$p$，则概率分布的基尼指数为：
$Gini(p)=2p(1?p)$

对于给定的样本集合$D$，其基尼指数为：
$Gini(D)=1?{\sum }_{k=1}^K(\frac{|C_k|}{|D|}{)}^2$
其中，$C_k$是$D$中属于第$k$类的样本子集，$K$是类的个数。

如果样本集合$D$根据特征$A$是否取某一可能值$a$被分割为$D_1$和$D_2$两部分，即：
$D_1=(x,y)\in D|A(x)=a$，$D_2=D?D_1$

则在特征$A$的条件下，集合$D$的基尼指数为：
$Gini(D,A)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)$

基尼指数$Gini(D)$表示集合$D$的不确定性，基尼指数$Gini(D,A)$表示经$A=a$分割后集合$D$的不确定性，基尼指数越大，样本集合的不确定性也就越大。

21. 朴素贝叶斯基本原理和预测过程

朴素贝叶斯法分类时，对给定的输入$x$，通过学习到的模型计算后验概率分布$P(Y=c_k|X=x)$，将后验概率最大的类作为$x$的类输出，后验概率计算根据贝叶斯定理进行：
$P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{{\sum }_{k}P(X=x|Y=c_k)P(Y=c_k)}$

由条件独立性假设可得：
$y=f(x)=argma{x}_{c_k}\frac{P(Y=c_k){\prod }_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)}{{\sum }_{k}P(Y=c_k){\prod }_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)}$
上式中的分母对所有$c_k$都是相同的，所以比较的时候只比较分母即可。

22. 朴素贝叶斯（naive Bayes）法的要求

朴素贝叶斯对条件概率分布作了条件独立性的假设。
$$\begin{gathered} P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=c_k) \\ ={\prod }_{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k) \end{gathered}$$

23. 分类算法列一下有多少种？应用场景

没有最好的分类器，只有最合适的分类器。
感知机、决策树、逻辑回归、贝叶斯分类器、支持向量机、K近邻、随机森林

决策树应用场景：因为能够生成清晰的树状图，当希望更好的理解数据时可使用决策树

逻辑回归应用场景：需要具有概率意义的输出，LR的参数代表每个特征对输出的二影响，可解释性强。LR的计算量小，存储占用低，可以在大数据场景中使用。LR虽然效果一般，但模型清晰。

贝叶斯分类器应用场景：需要一个比较容易解释，而且不同维度之间相关性较小时，可以高效处理高维数据，但结果不能保证

支持向量机应用场景：在很多数据上表现优秀，可以尝试。

KNN应用场景：需要一个特别容易解释的模型的时候

随机森林应用场景：一种集成方法，能够解决大规模数据集的问题，还可以给变量重要性进行排序，刚拿到数据集不知道用什么方法的时候，也可尝试随机森林。

24. 生成模型和判别模型基本形式，有哪些？

典型的生成模型有：朴素贝叶斯法和隐马尔可夫模型。
生成模型：
$P(Y|X)=\frac{P(X,Y)}{P(X)}$

典型的判别模型有：k近邻法、感知机、决策树、逻辑斯蒂回归模型、最大熵模型、支持向量机、提升方法和条件随机场。
判别模型表示给定输入的$X$产生输出$Y$的生成关系。

本文参考文献：
机器学习算法的应用场景

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖