任务225: 时序模型
随时间维度变化的
每时每刻有相关性(t时刻数据t+1时刻数据有相关性)
时序数据长度不确定
时序数据:如股票价格、语音、文本、温度


任务226: HMM的介绍
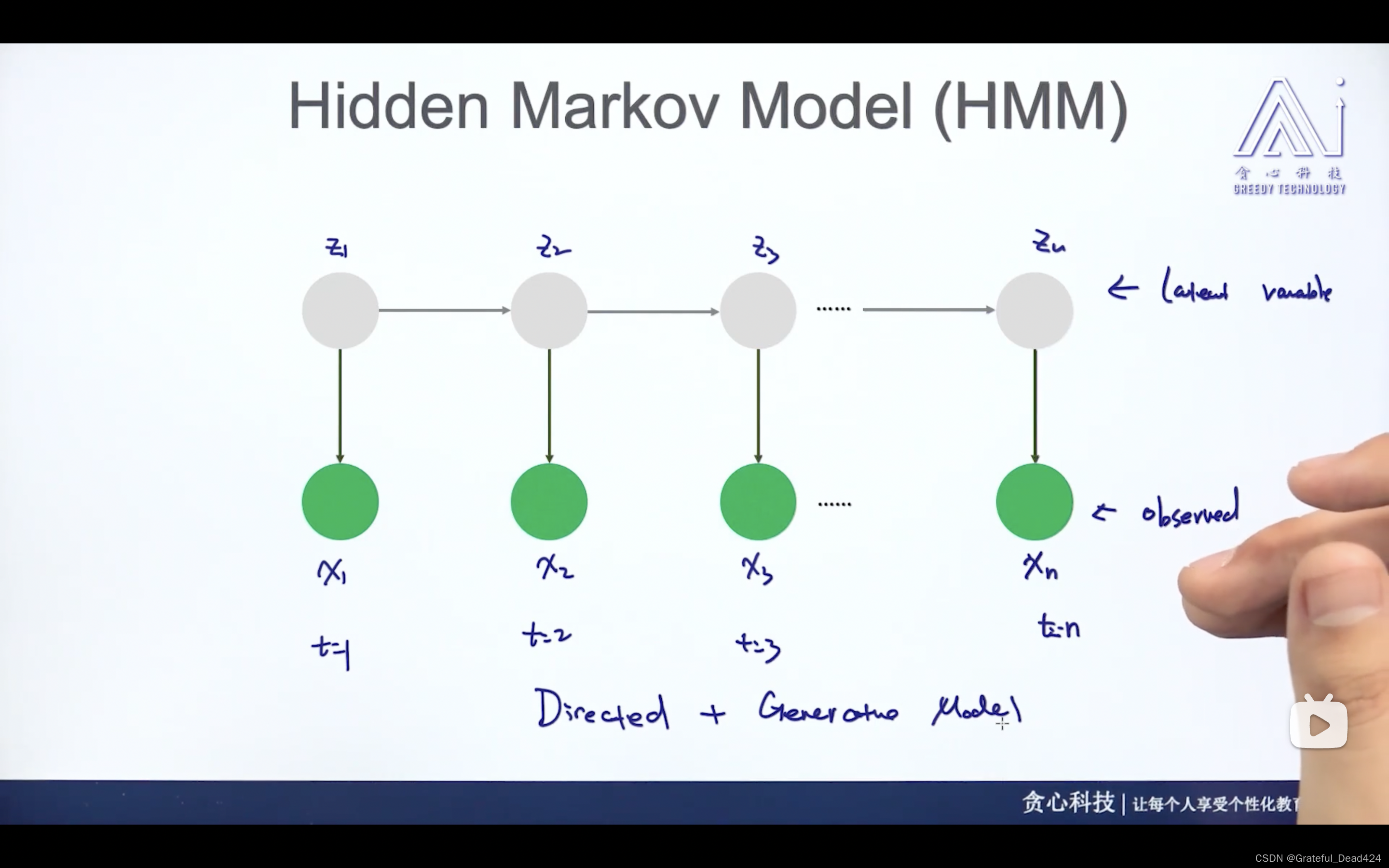
观测值、隐式变量
z是一个隐式的状态
可以是生成模型,从状态生成观测值
也可以是判别模型
任务227: HMM的应用例子
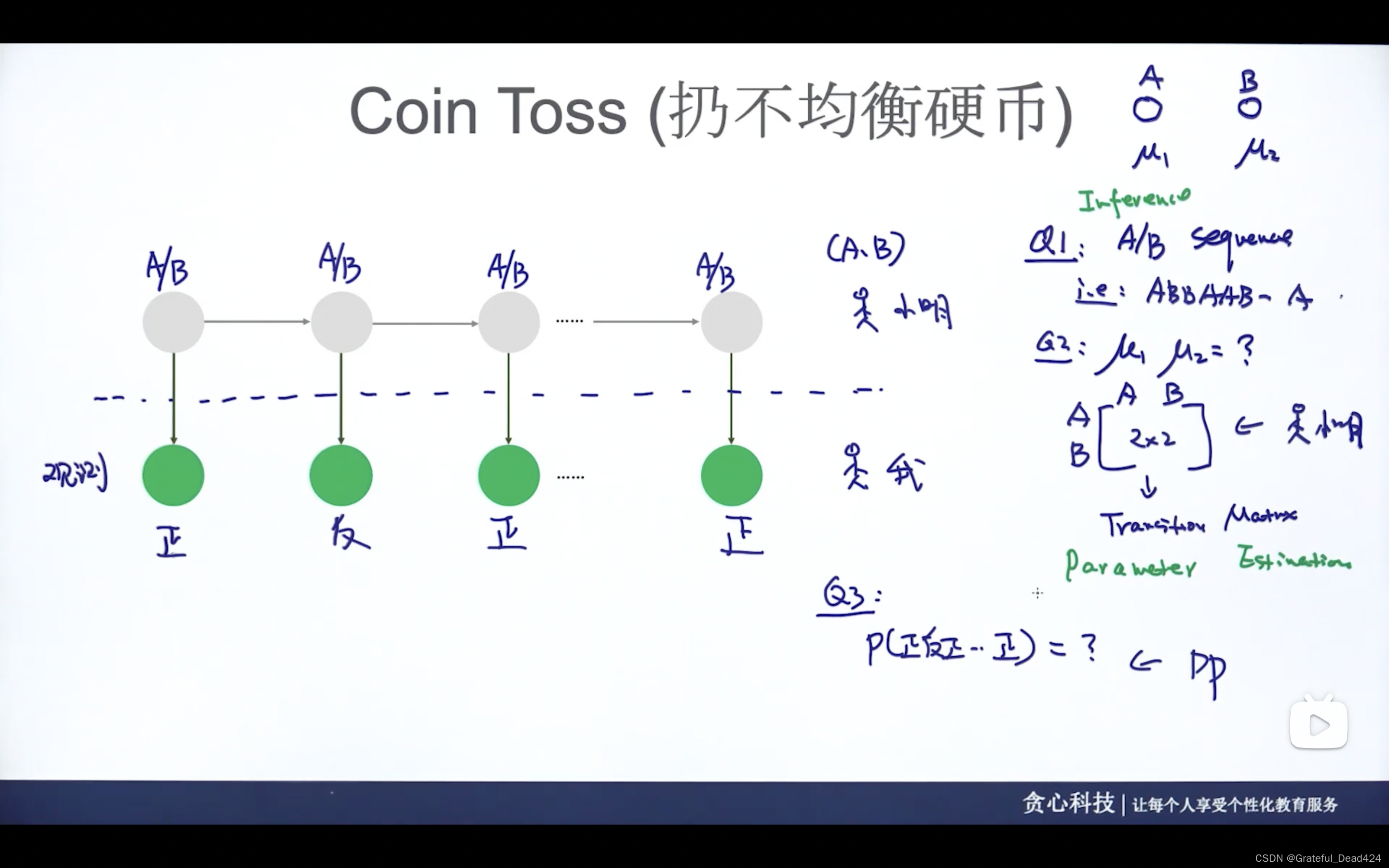
掷硬币案例
A硬币出现正面的概率是
μ
1
\mu_{1}
μ1?
B硬币出现正面的概率是
μ
2
\mu_{2}
μ2?
小明和我隔着一块不透明的布
小明有自己的顺序投A还是投B,我只能看到硬币最后是正面还是反面朝上
由此产生两个问题
(1)inference问题
(2)parameter estimation参数估计问题
(3)P(正反正…),计算边缘概率
能不能通过观测值估算出所有的参数,能不能通过参数知道抛硬币的次序
词性标注案例

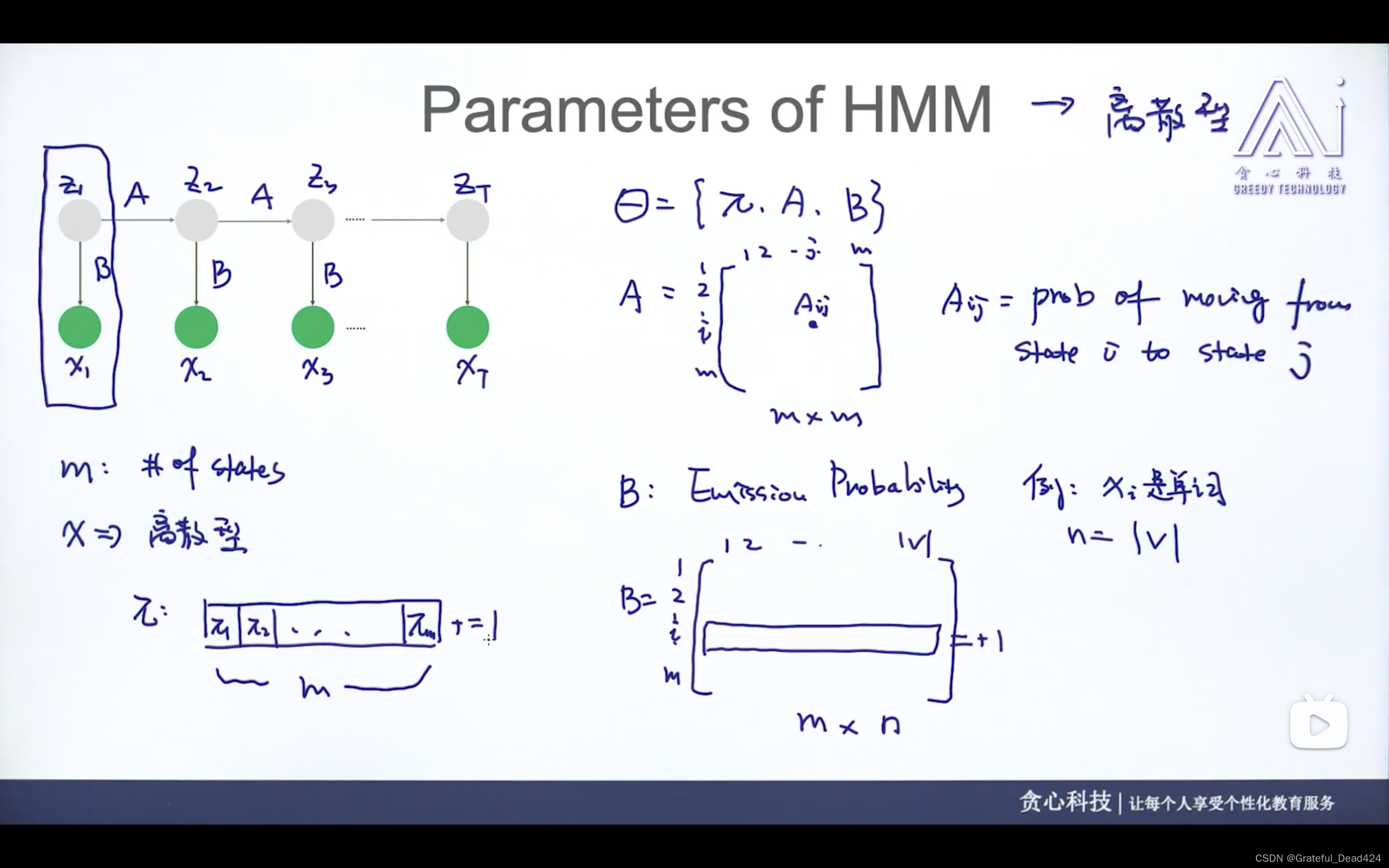
任务228: HMM的参数
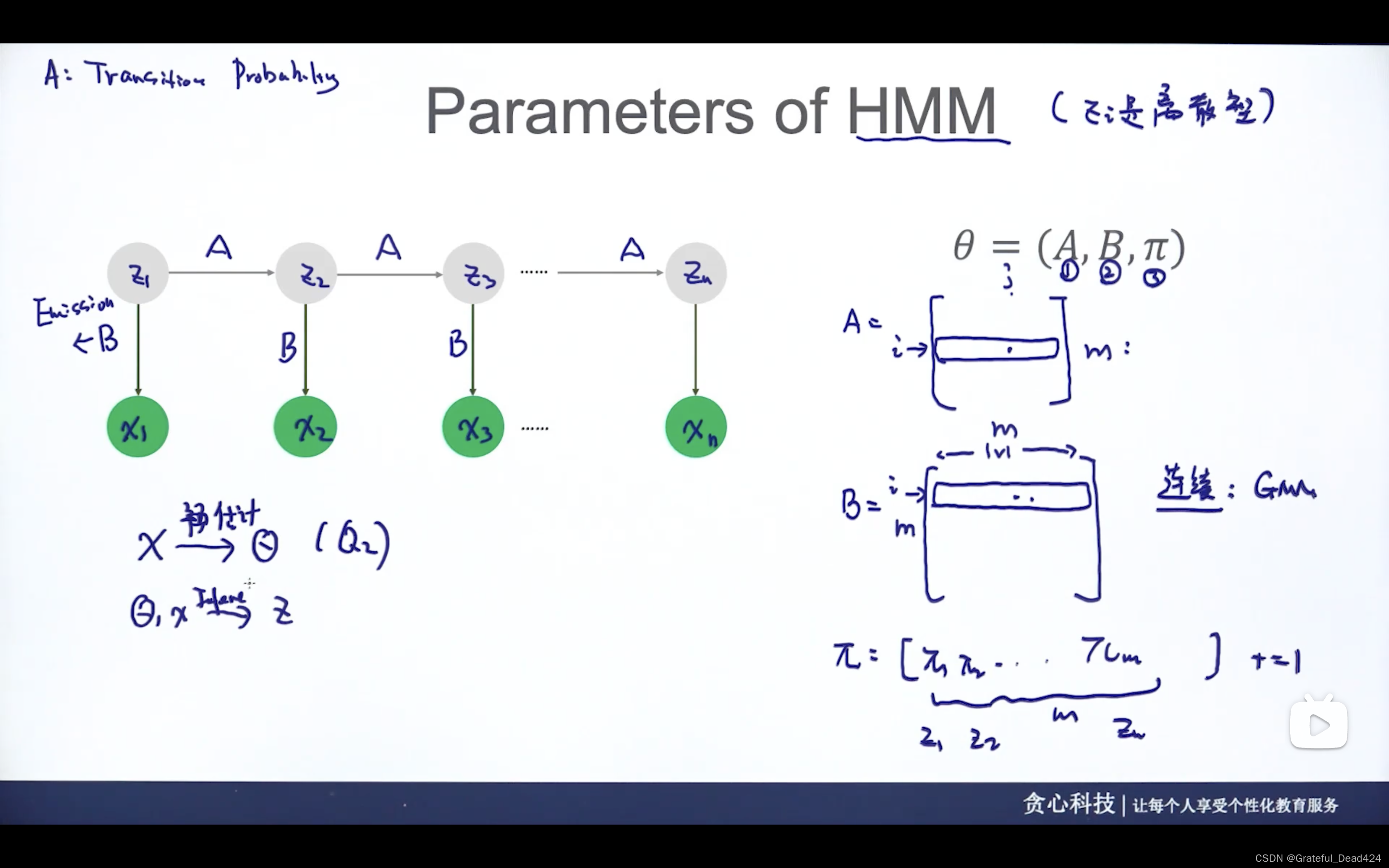
A——状态转移的概率,从一个状态变成另一个状态
B——生成的概率,某一个状态下看到某个观测值的概率
π
\pi
π——某个状态是句首单词状态的概率
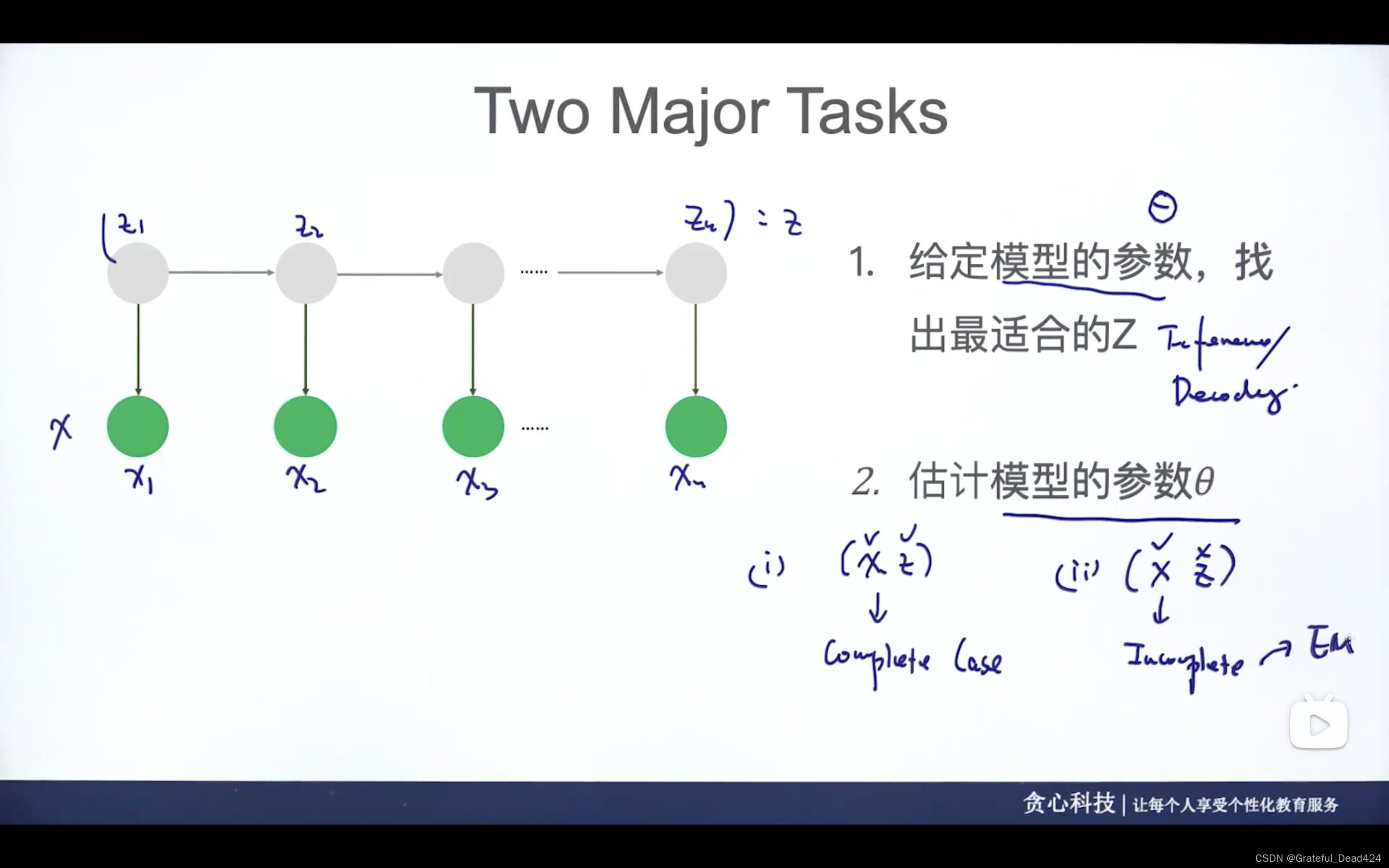
估计参数
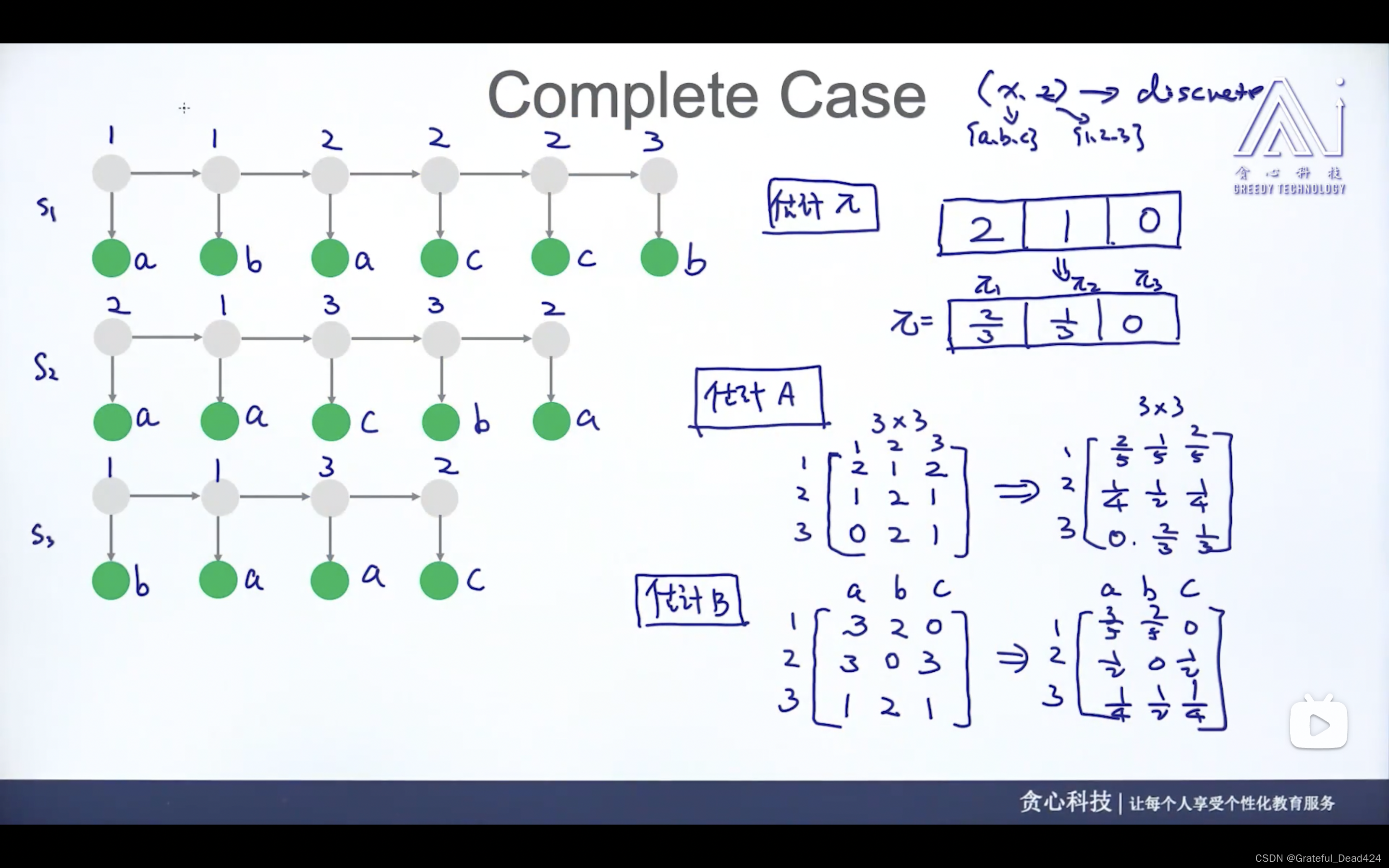
(1)(x已知,z已知)complete case——>mle估计参数
(2)(x已知,z未知)incomplete case——>EM算法
任务229: HMM中的Inference问题
已知观测值、已知参数的情况下讨论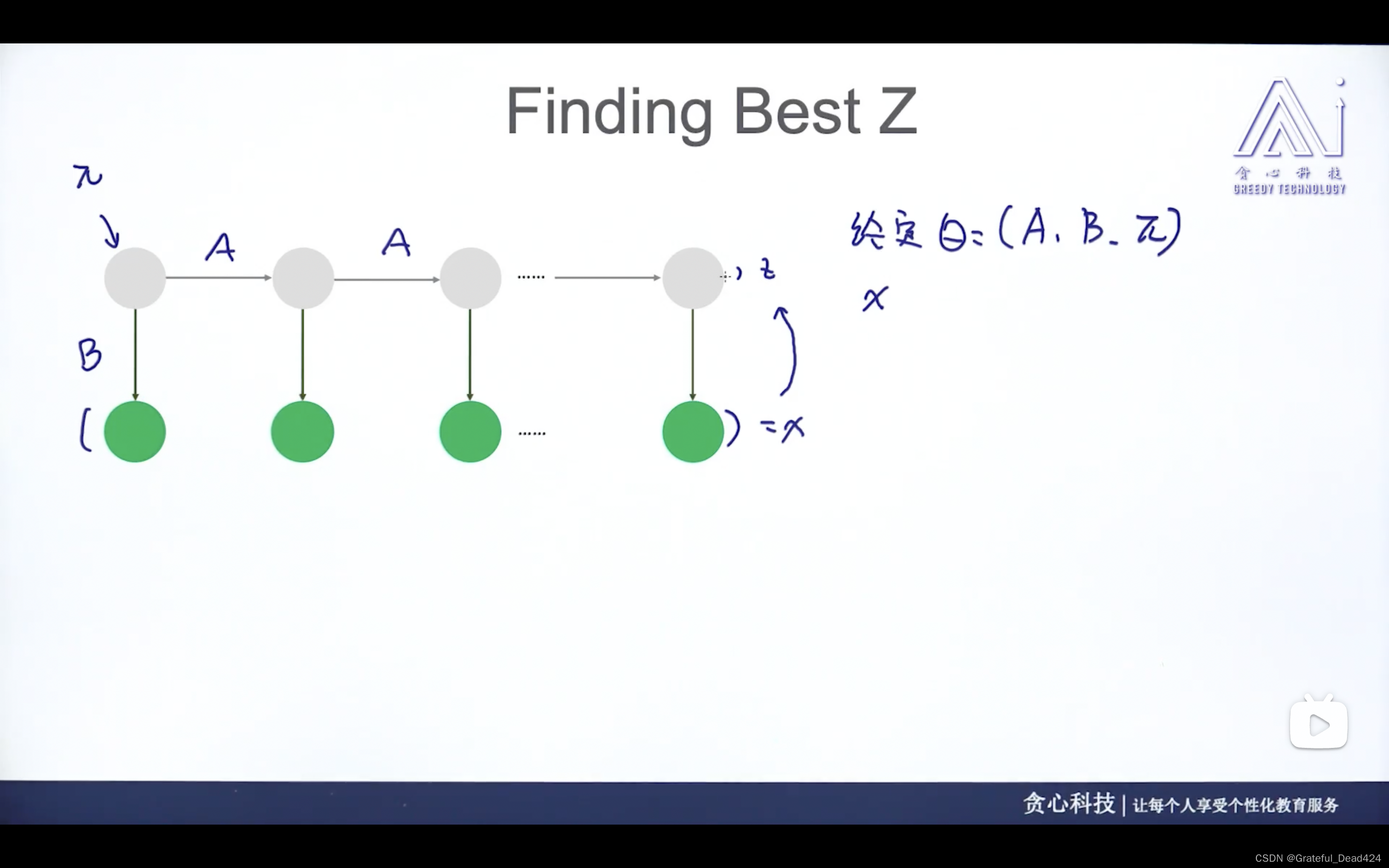
第一种方法:使用枚举法
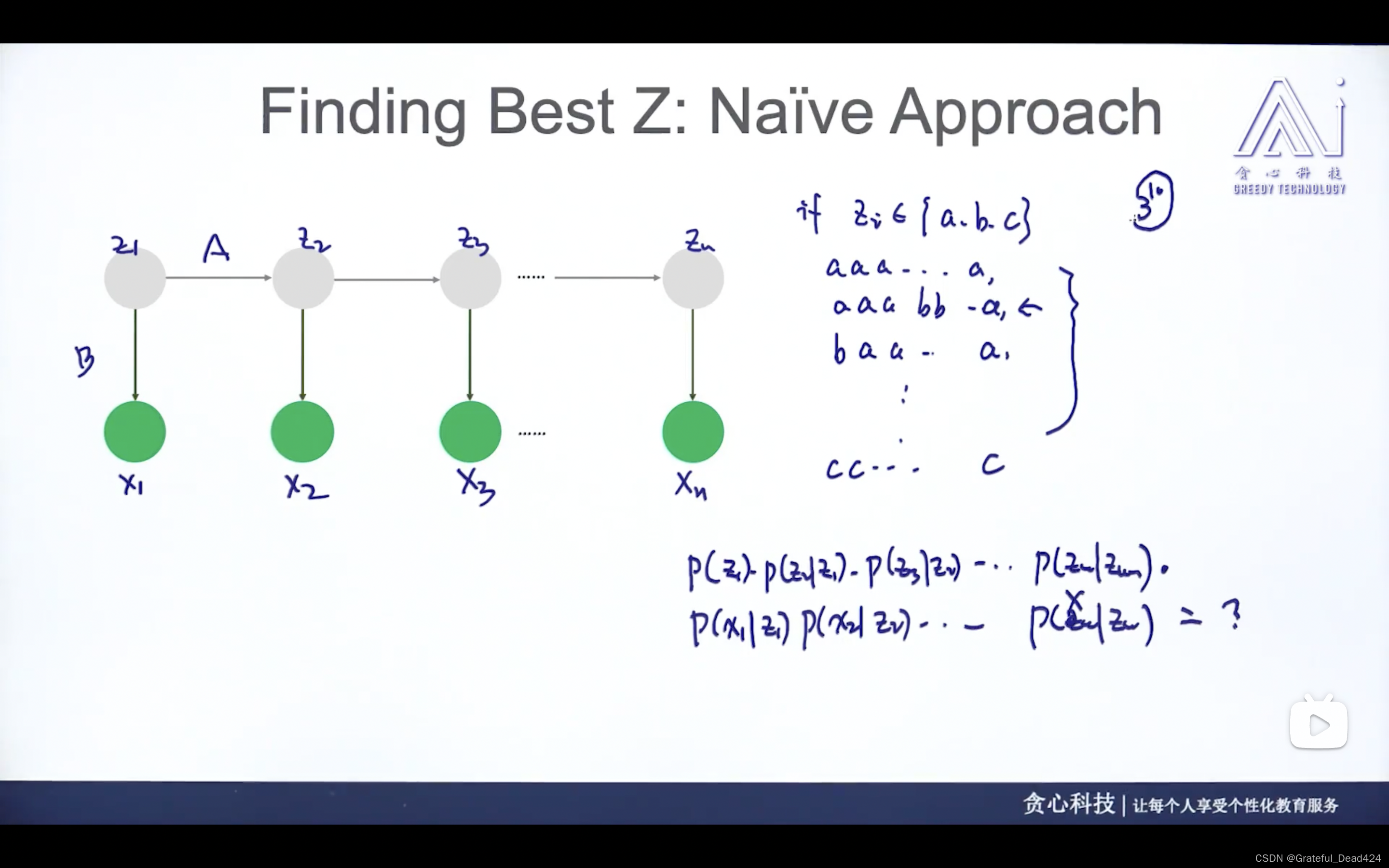
枚举z不同情况的组合
第二种方法:使用维特比算法
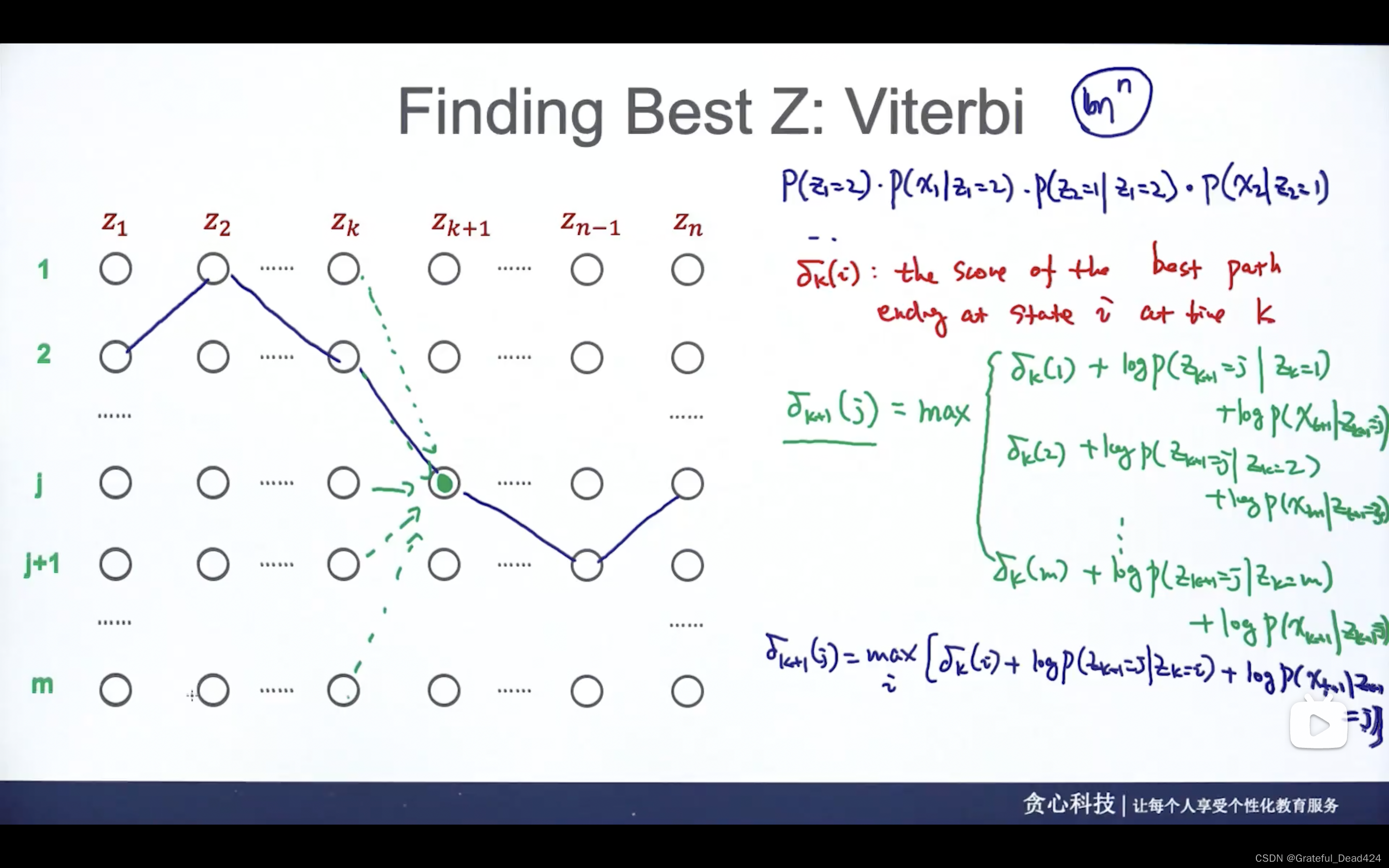
动态规划适合解决指数级别的复杂度,但可以通过存储中间的过程来去减轻计算量
维特比算法为什么适合HMM?
HMM有限制条件——隐式变量
z
i
z_{i}
zi?只会和前后
z
i
z_{i}
zi?有联系

从左到右,每一列填好,找出最后一列哪个结点分数最大,反向把整条路径找出来
任务230-232: HMM中的F B算法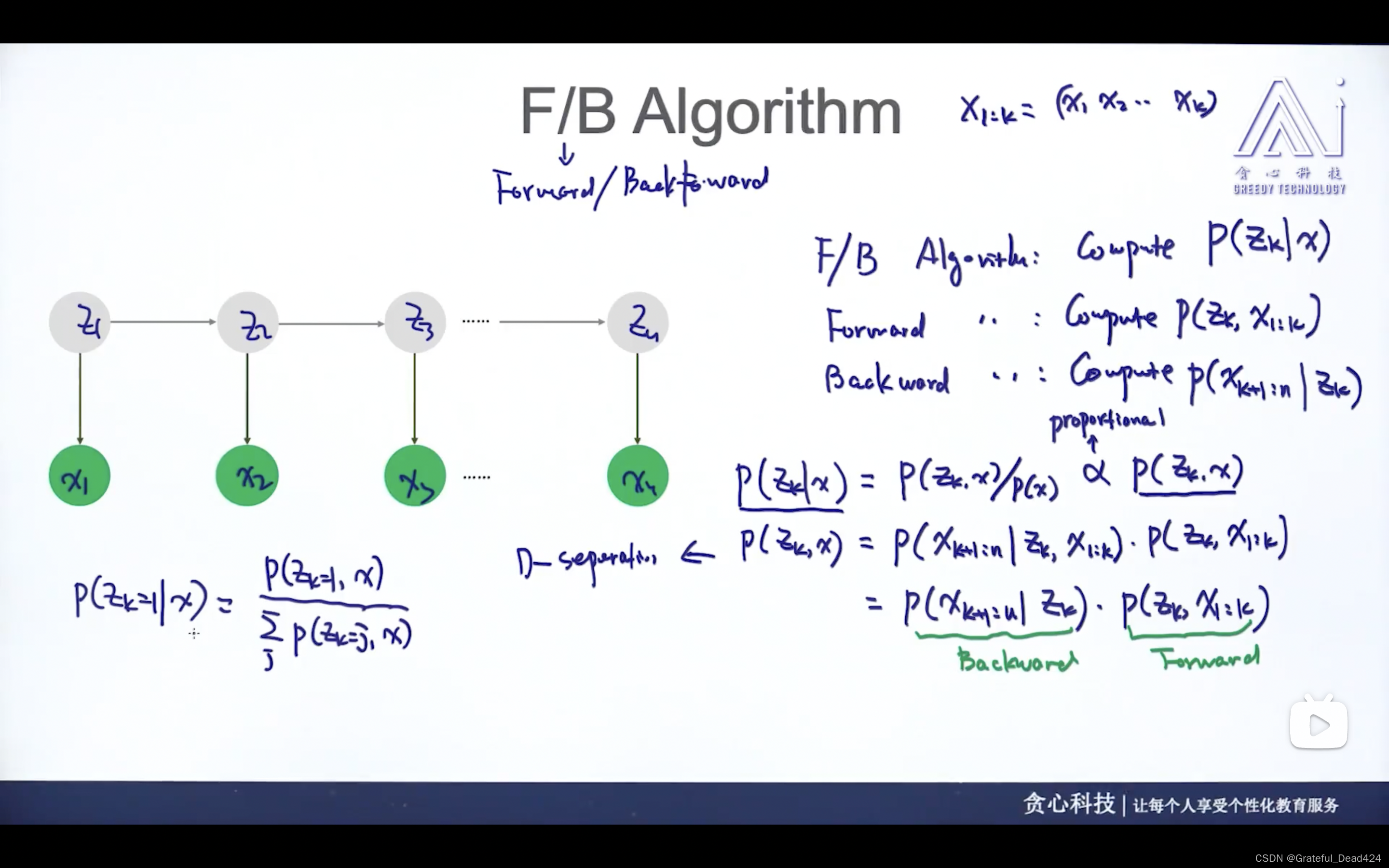
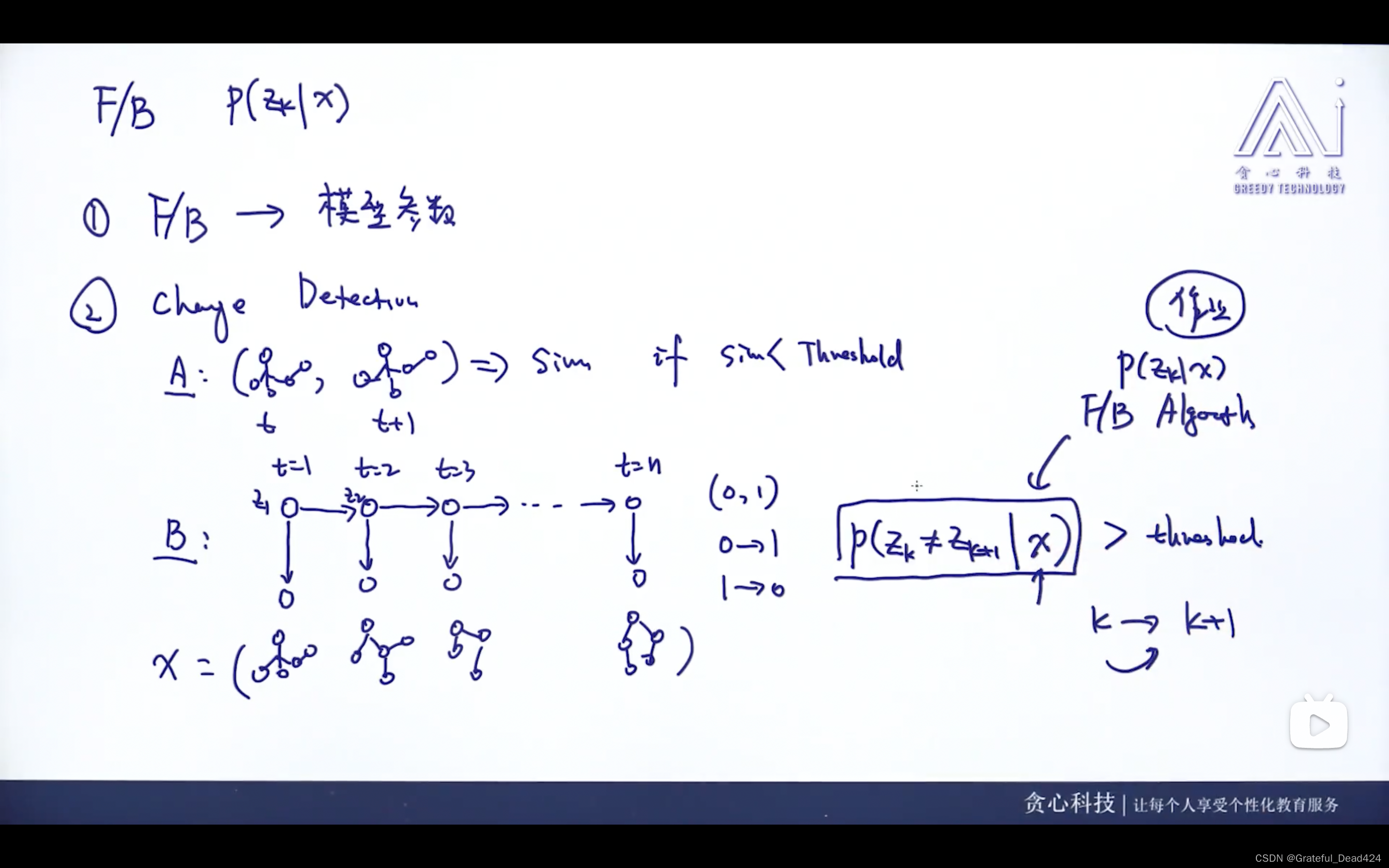
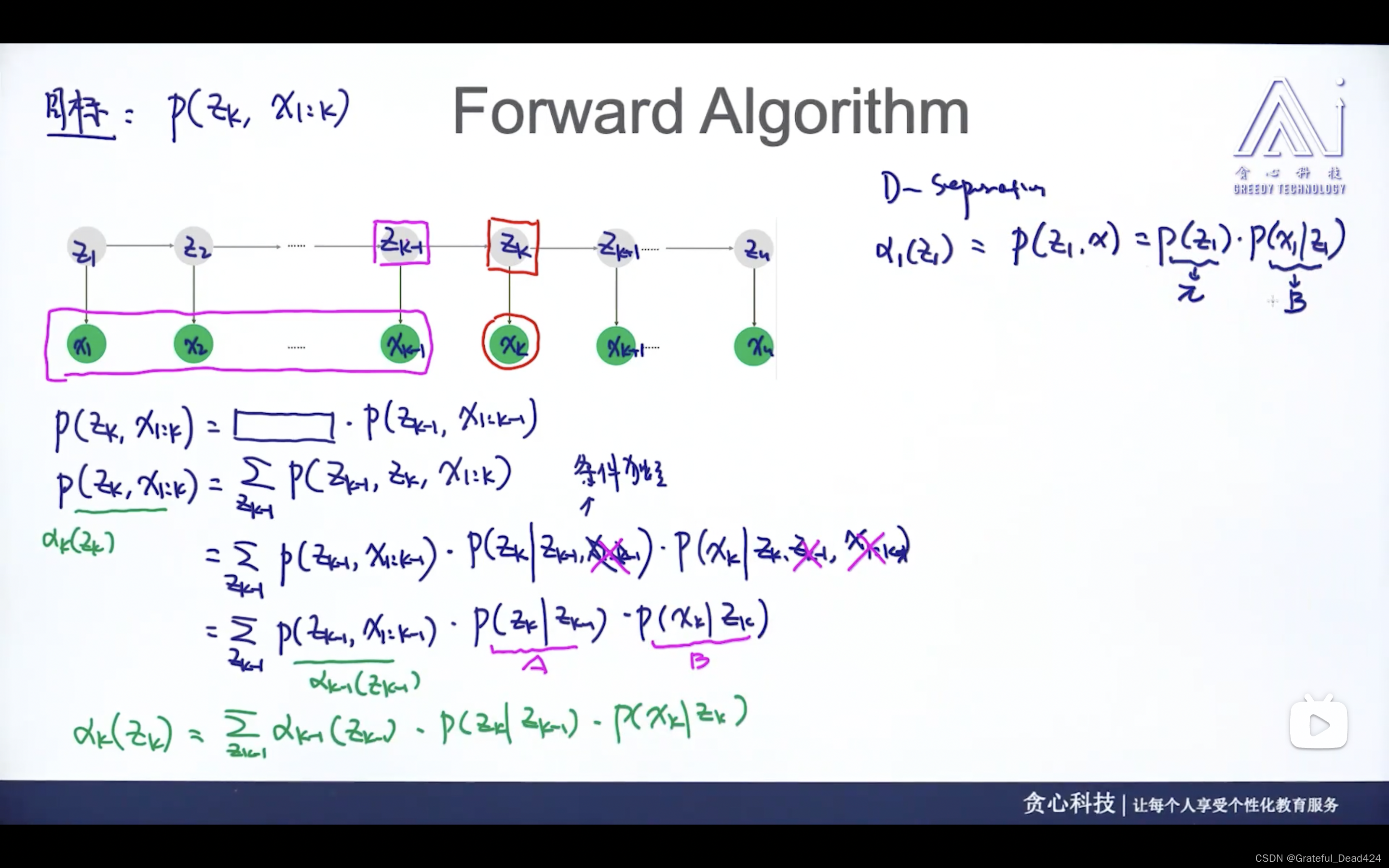
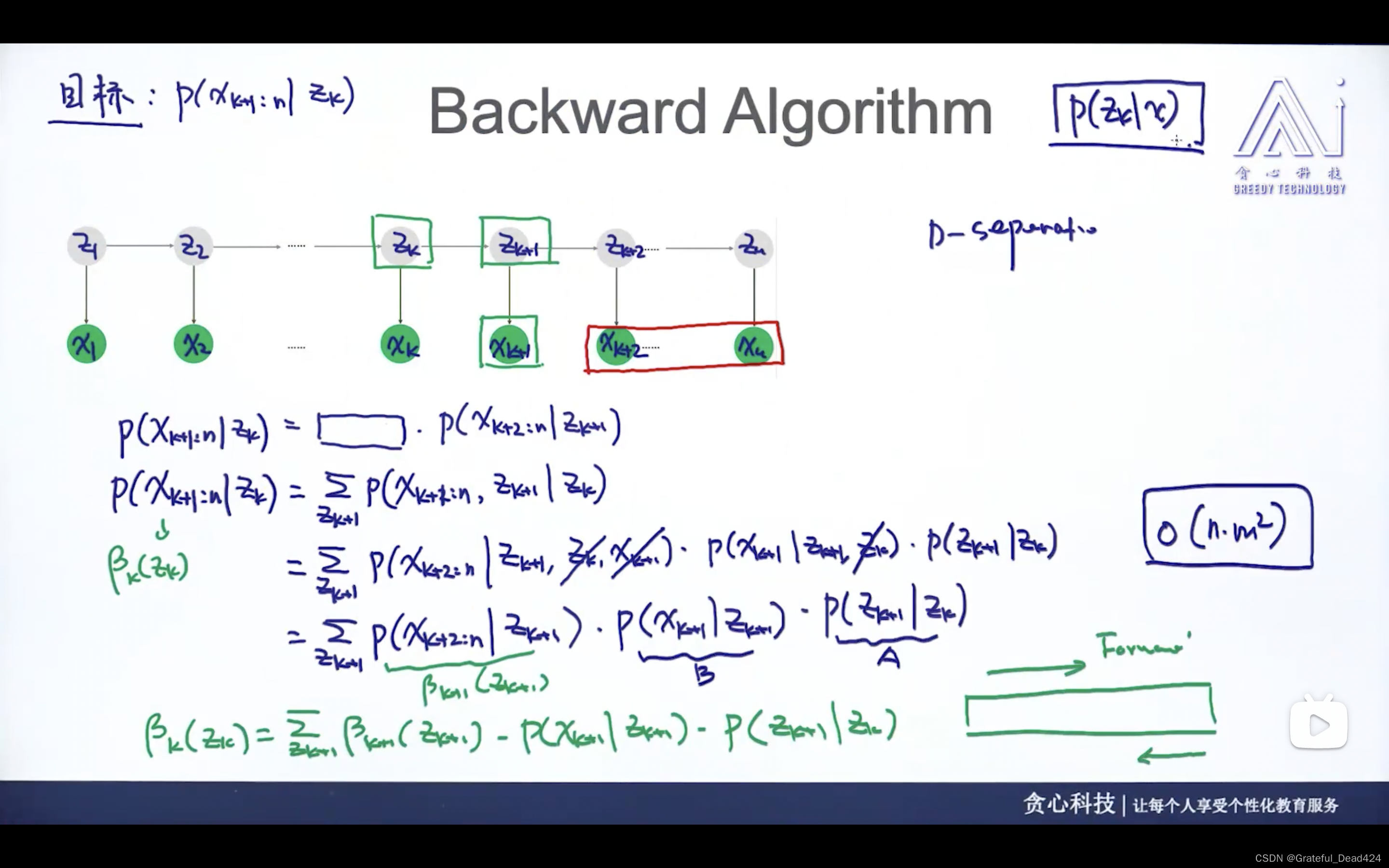
通过forward和backward算法,可以计算P( z k z_{k} zk? ∣ | ∣ x x x)的概率,方便后续的参数估计
任务233: Data Representation

原先的特征存在的问题
(1)冗余
(2)噪音
(3)有些特征不需要
更低维的空间有更好的特征表示方法
任务234: Latent Variable Models(隐变量模型)
隐变量模型——>EM算法解决掉
HMM,GMM(kmeans是其特例)都是经典的隐变量模型
传统逻辑回归(x,y)先在多了一个变量z——隐变量
隐变量gender、eye color、hair color、pose生成图片
x的维度比z的维度更高
现有z后有x
z之间有相关性
x之间没有相关性
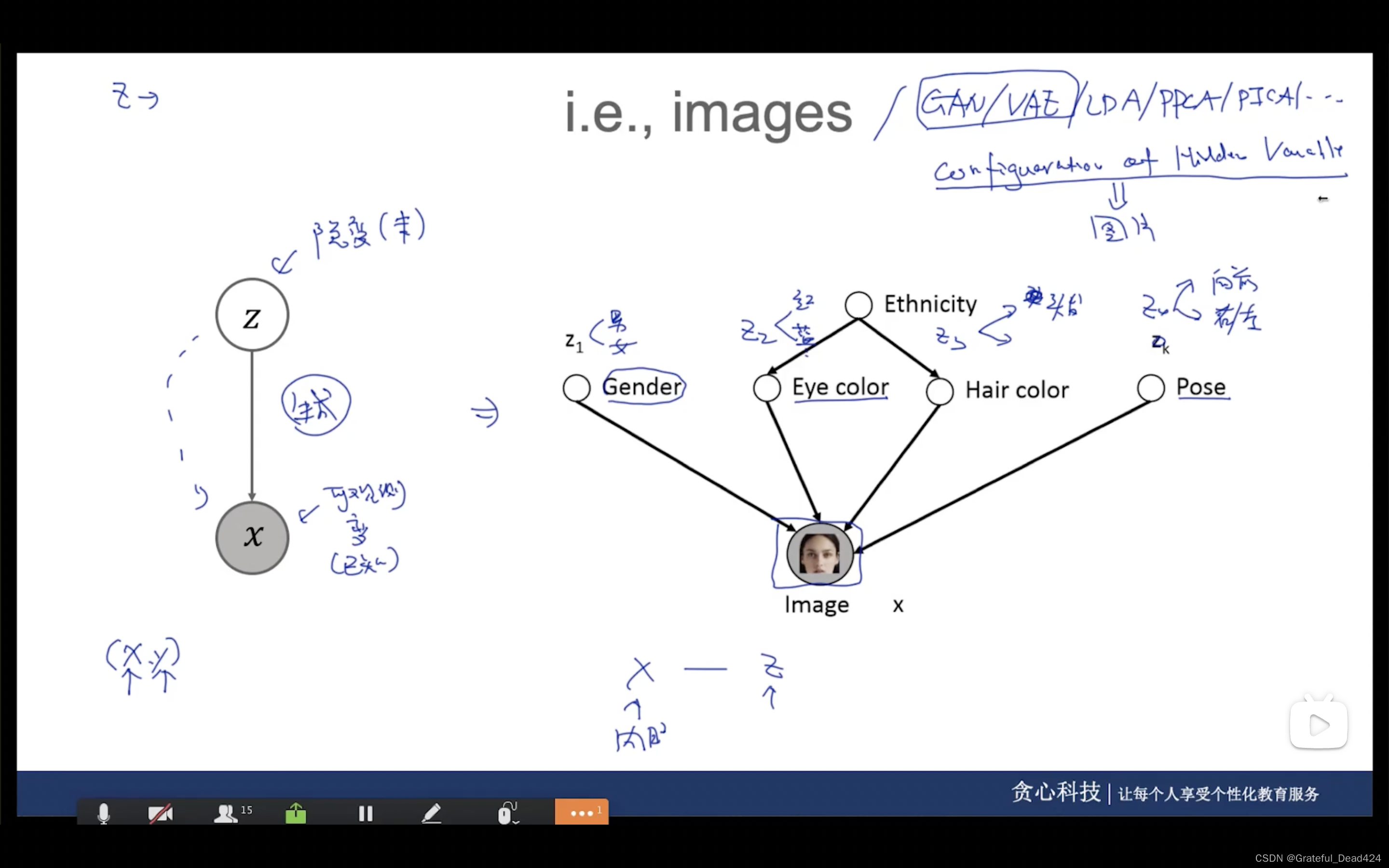
任务235: Complete vs Incomplete Case
参数估计时

任务236: MLE for Complete and Incomplete Case

任务237: EM Derivation



任务238: Remarks on EM
EM算法不能保证全局最优解,只能保证局部最优解
EM算法,严格递增(一定会converge收敛)

任务239: K-means
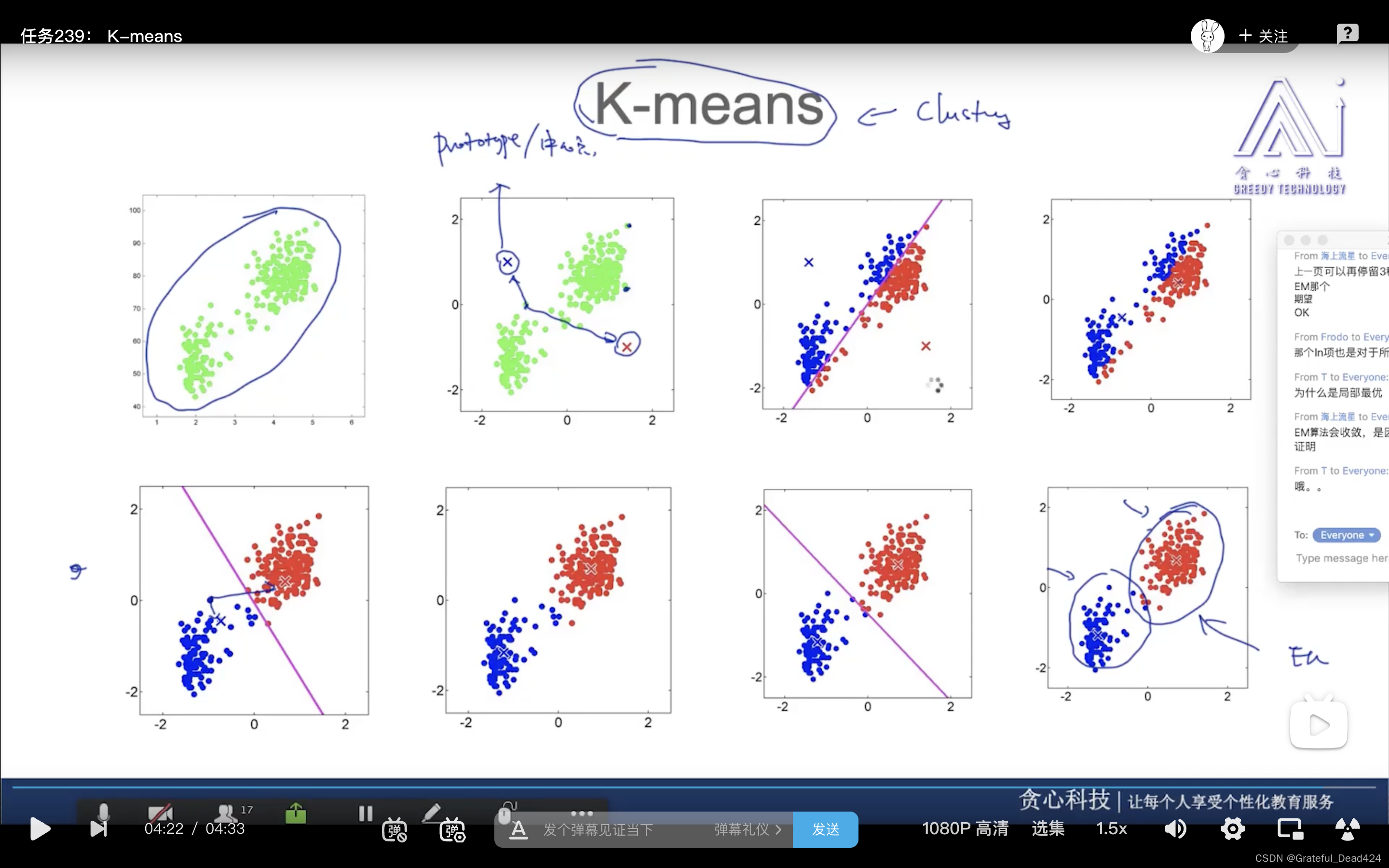
任务240: K-means Cost Function

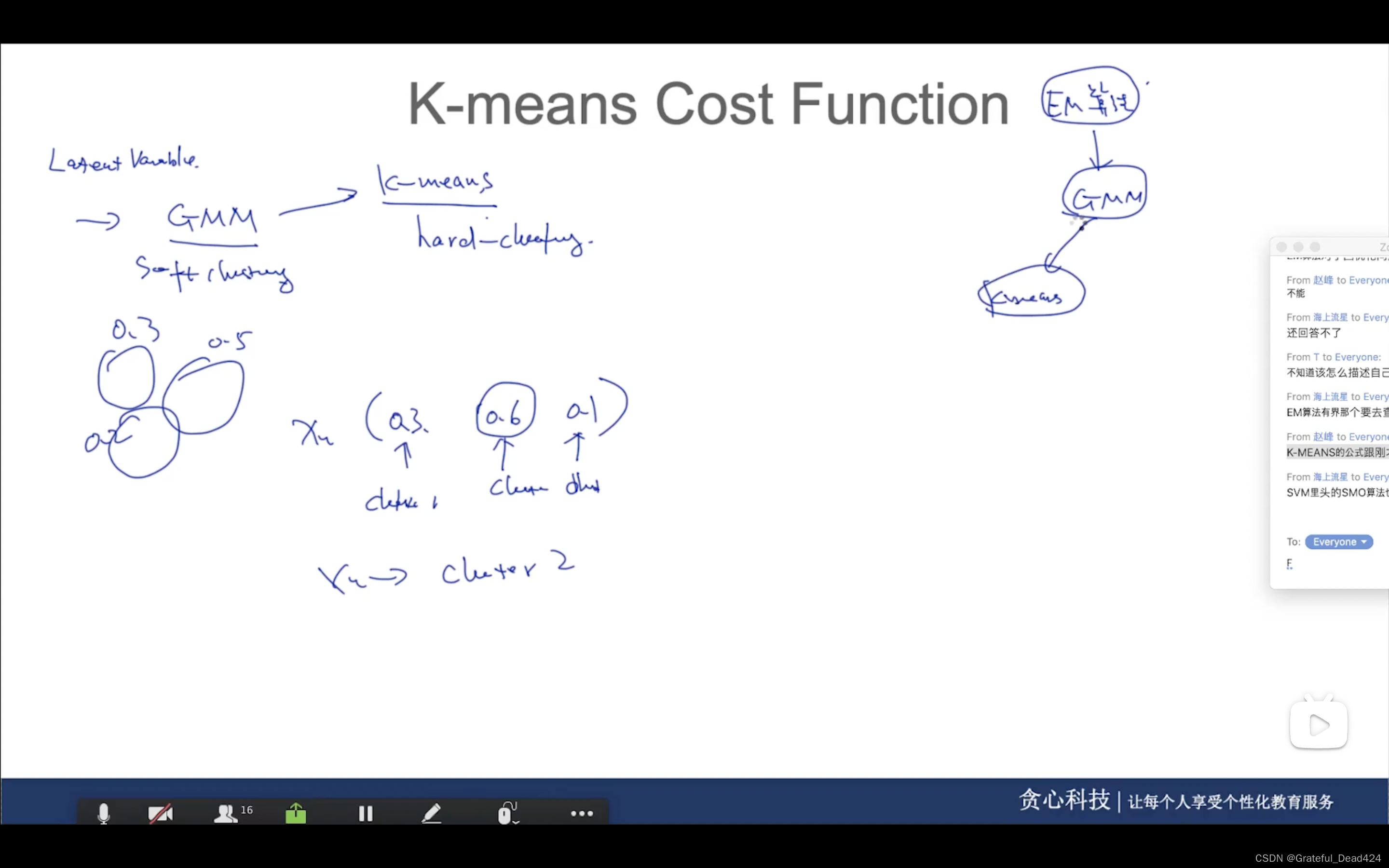
任务241: MLE for GMM
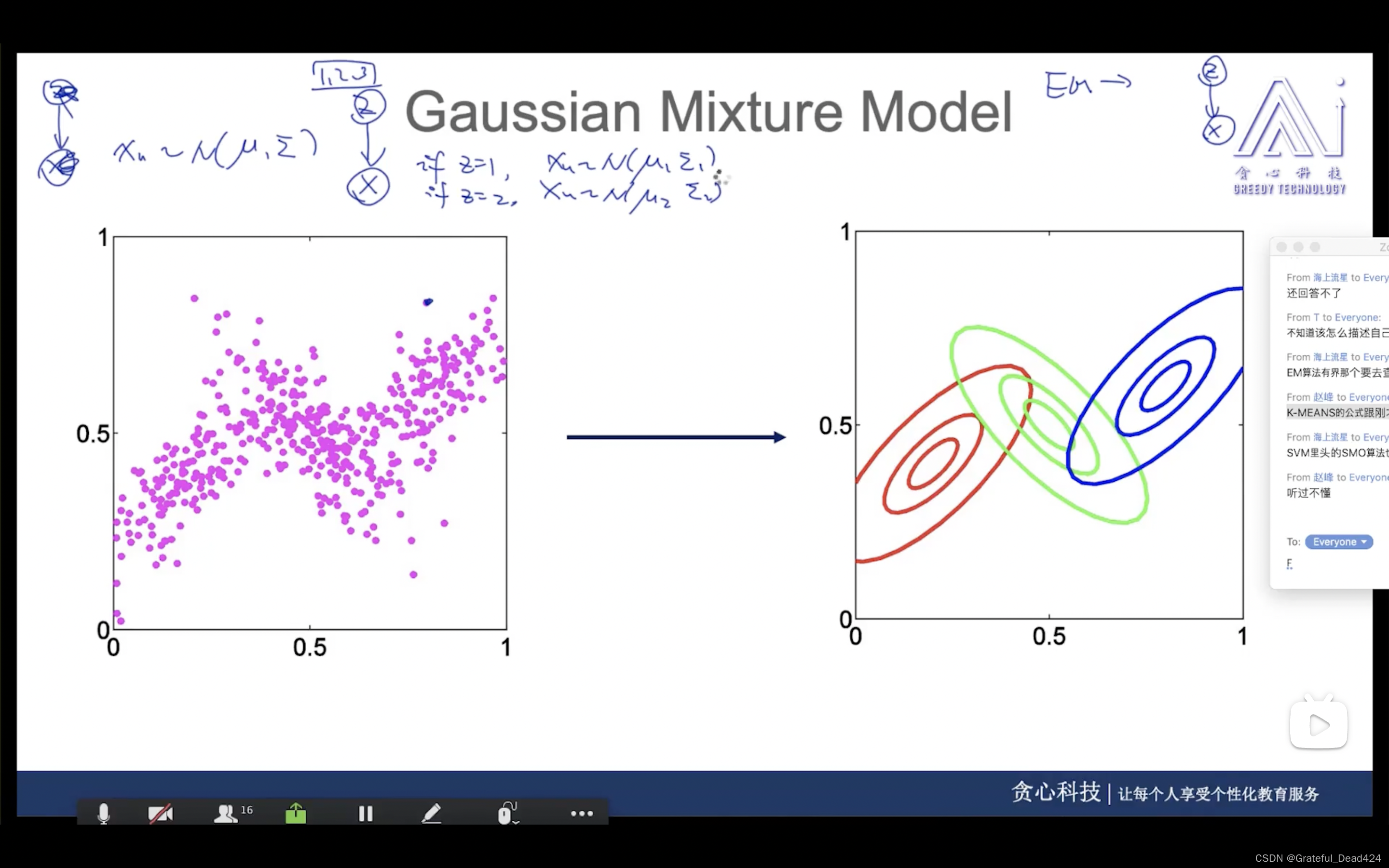

没有
∑
\sum
∑就是kmeans
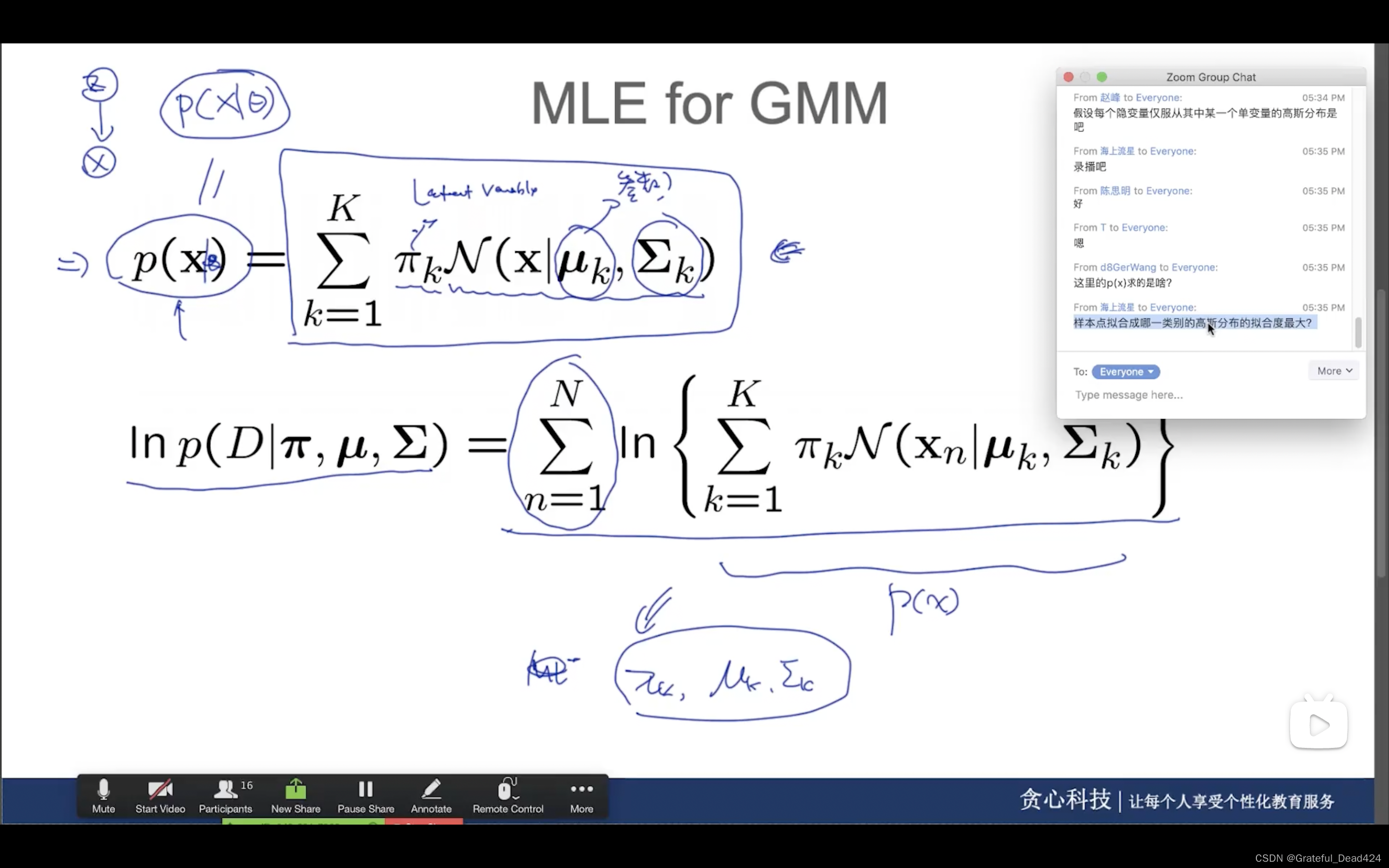
任务244: HMM中的参数
任务245: Complete vs Incomplete Case

任务247: Incomplete Case
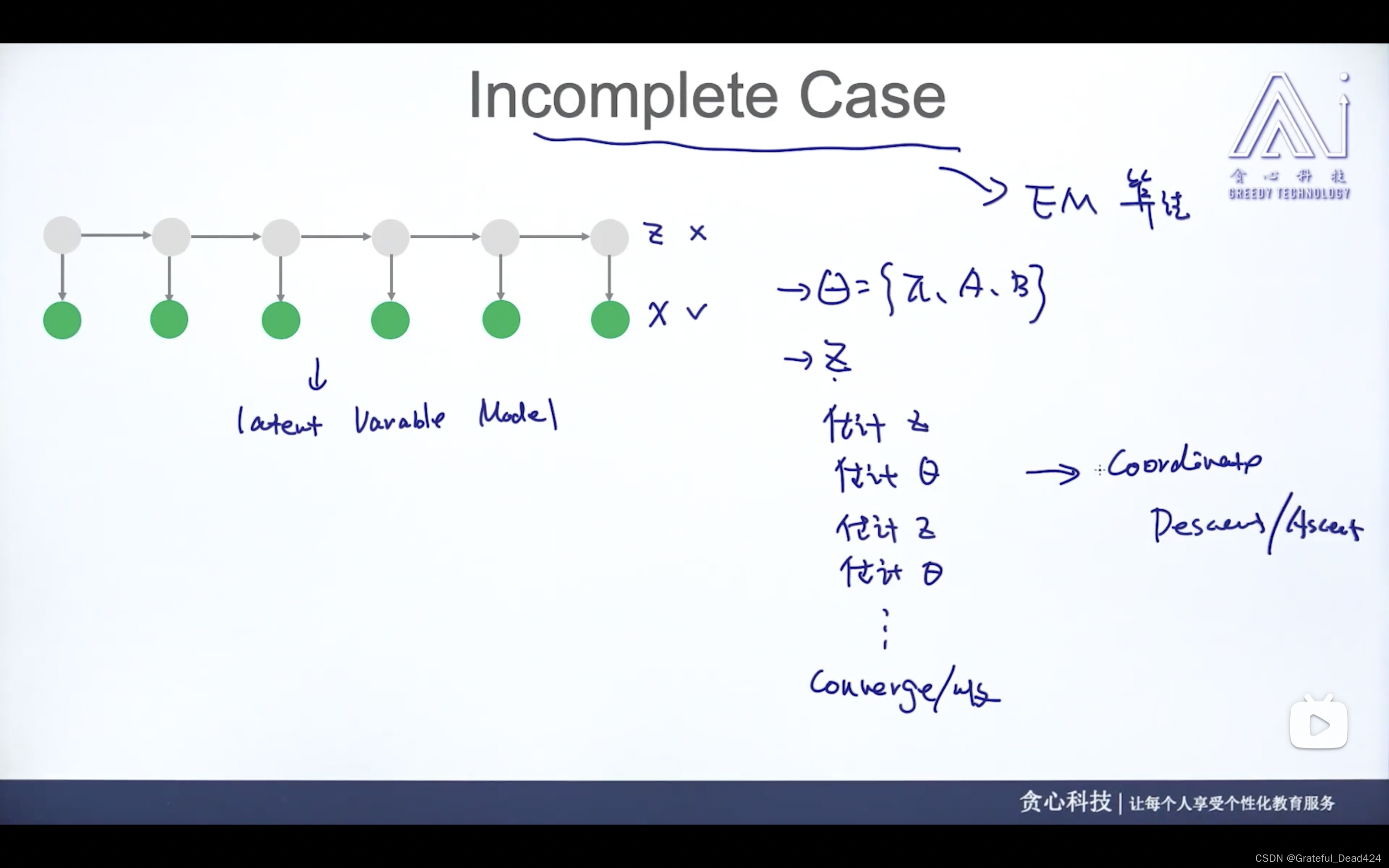
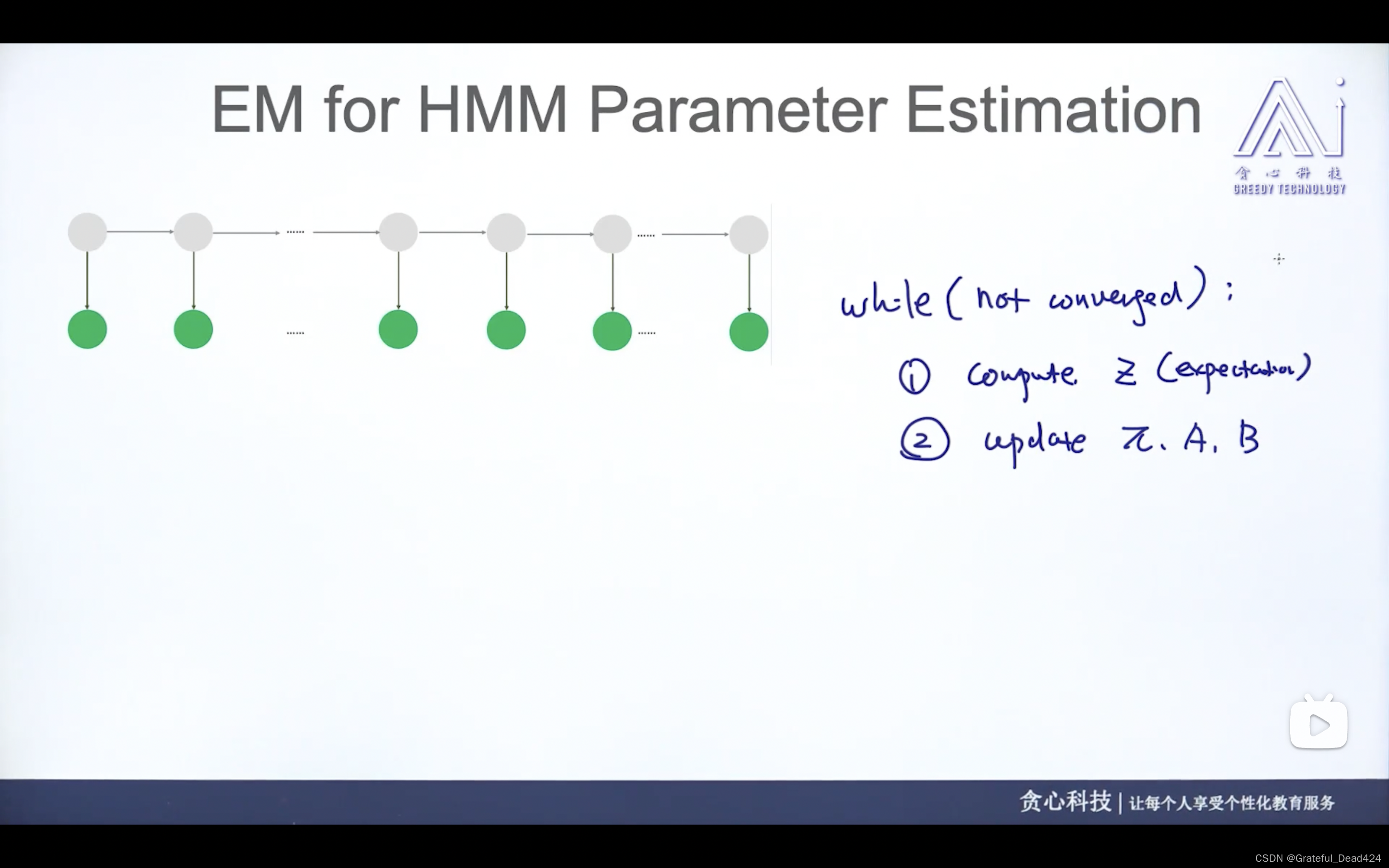
任务248: EM算法回顾
先求z的期望,再求ln这个式子

任务249: F B算法回顾
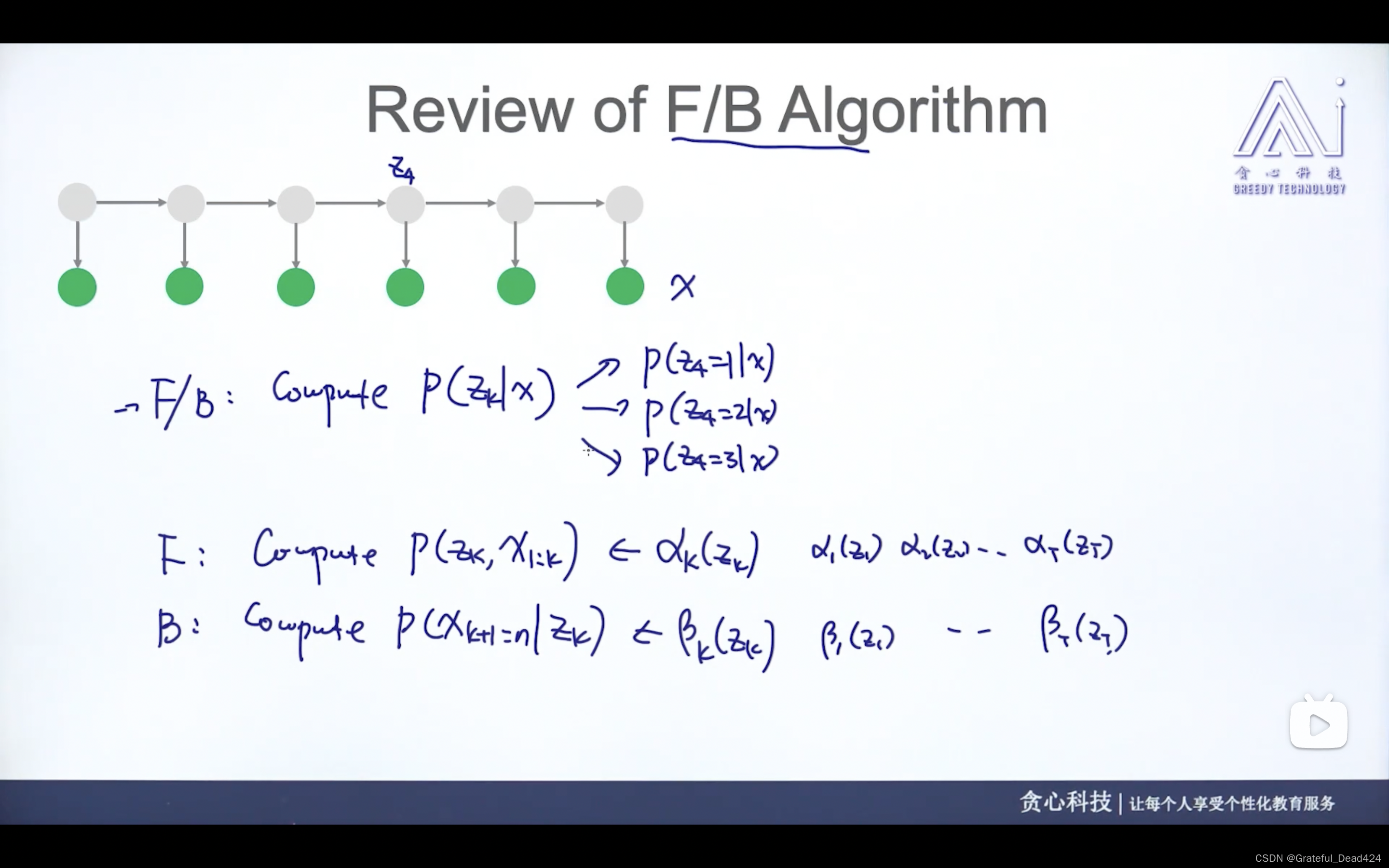
任务250: 估计PI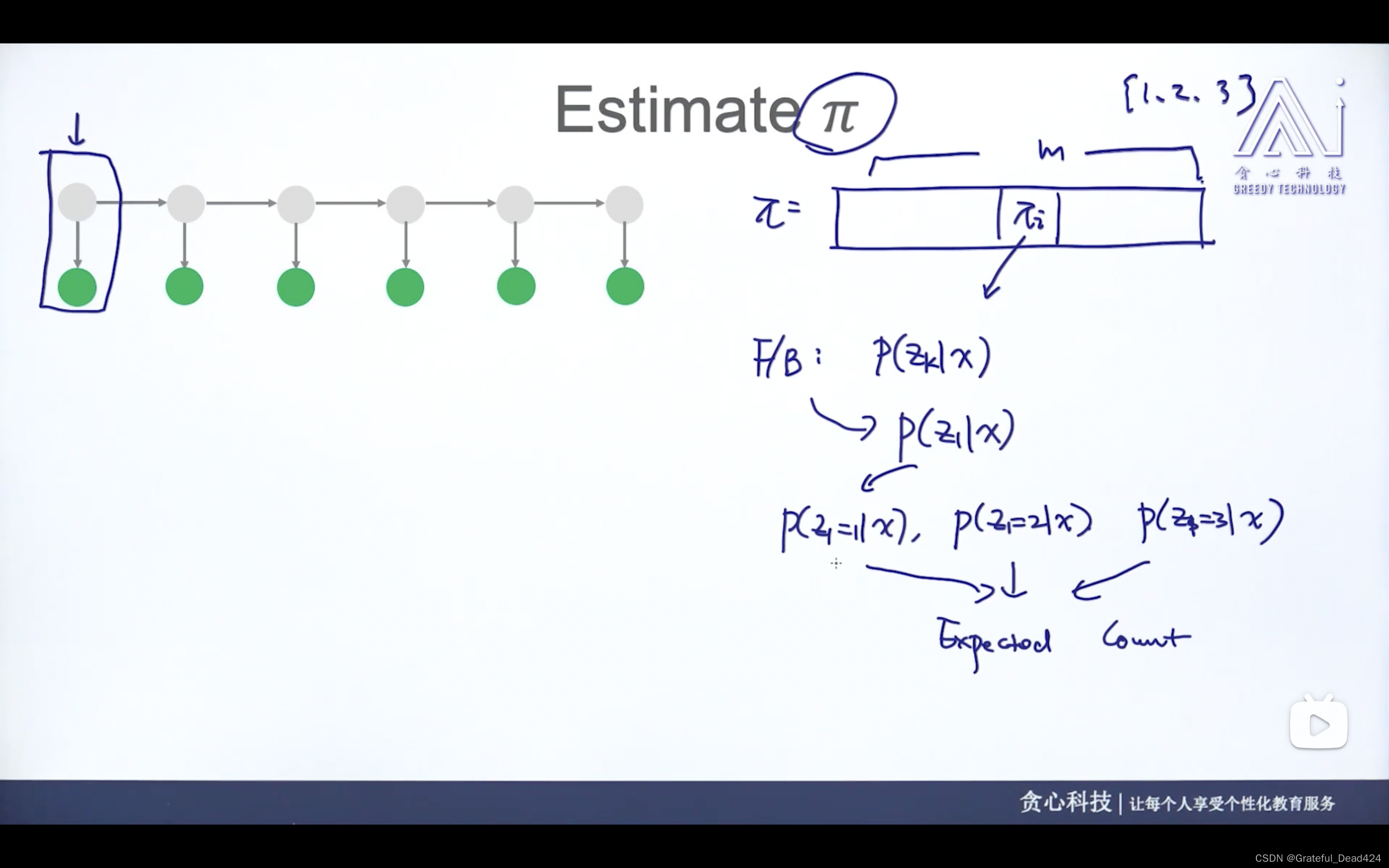
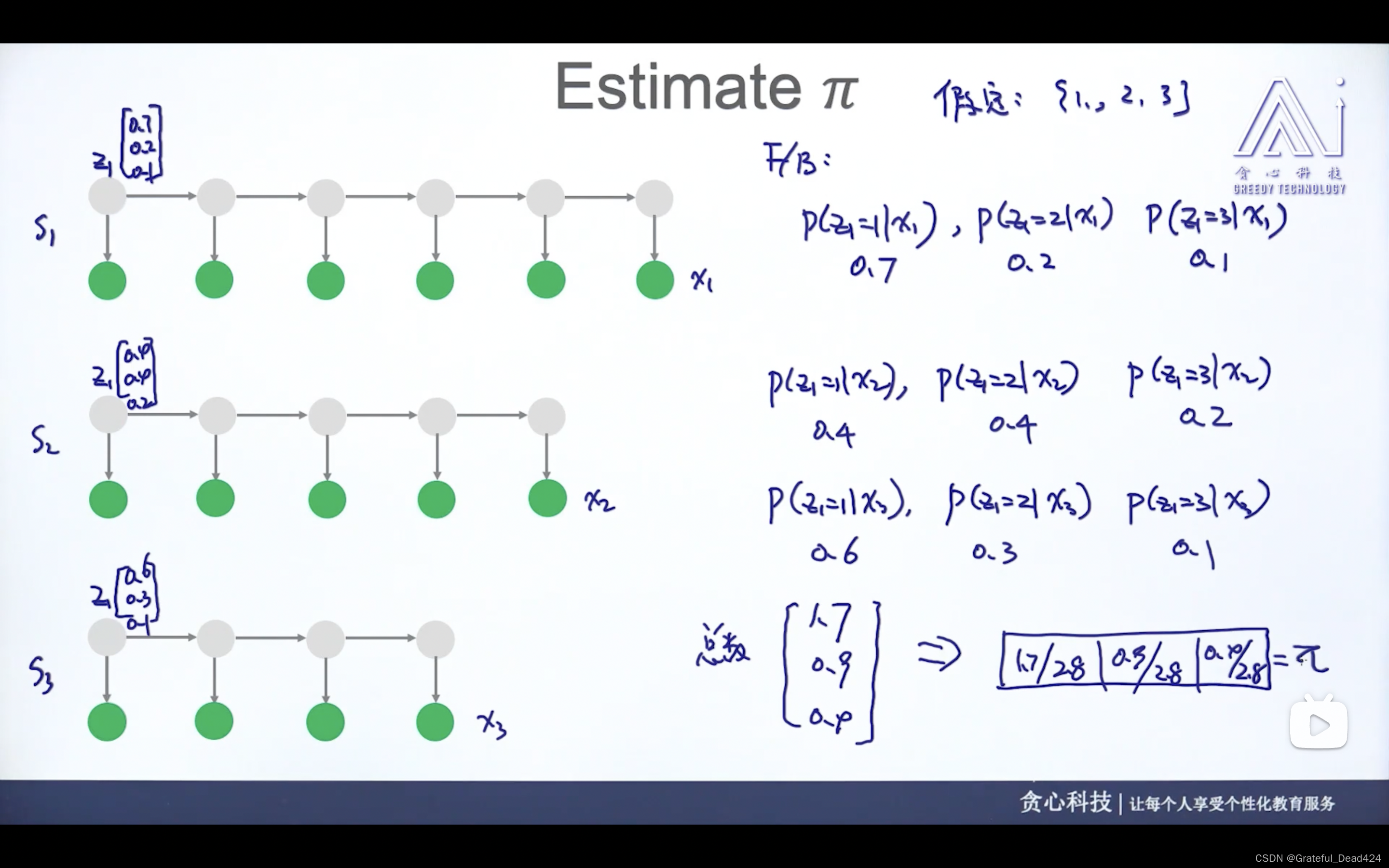
任务251: 估计B

任务252: 估计A

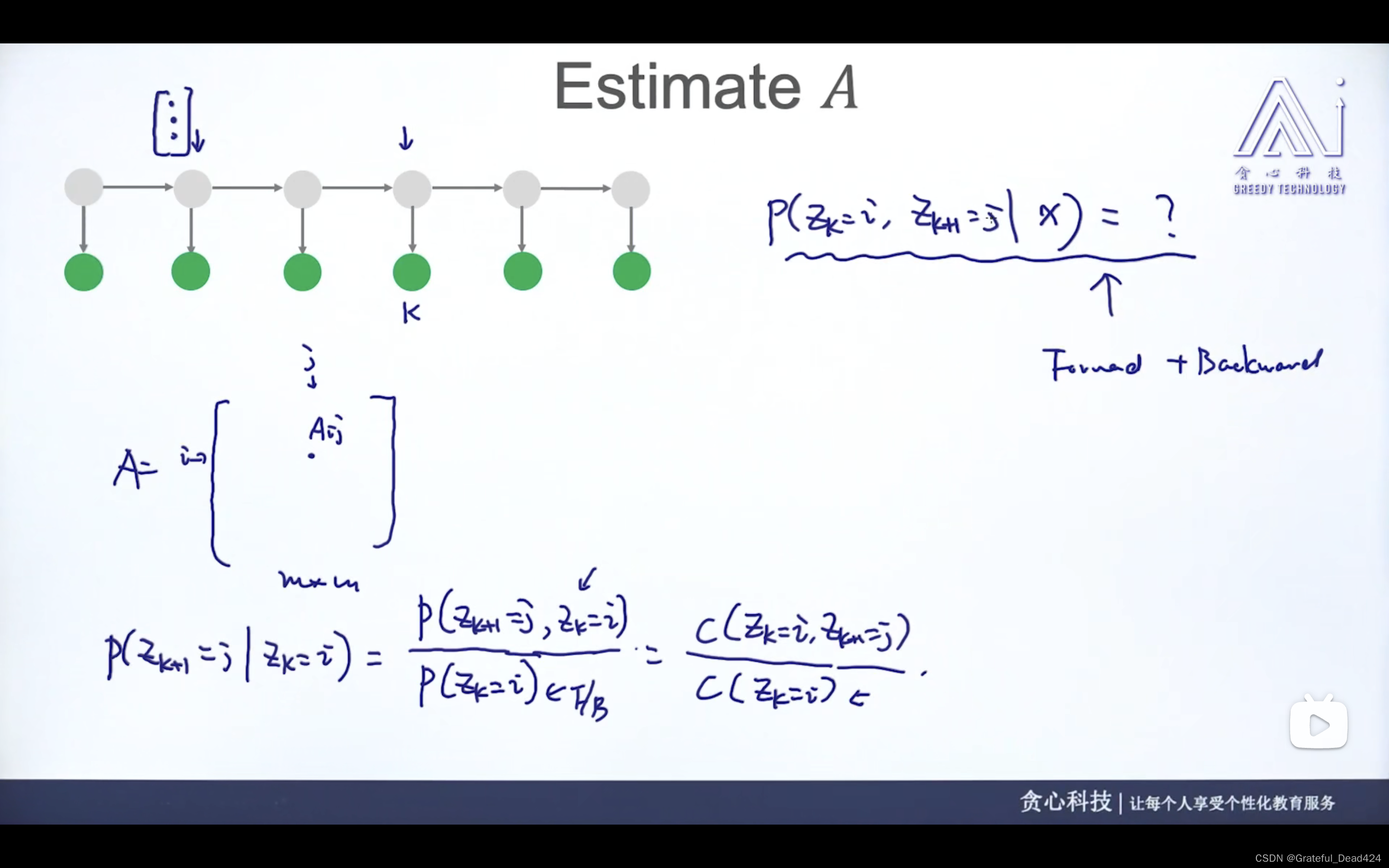
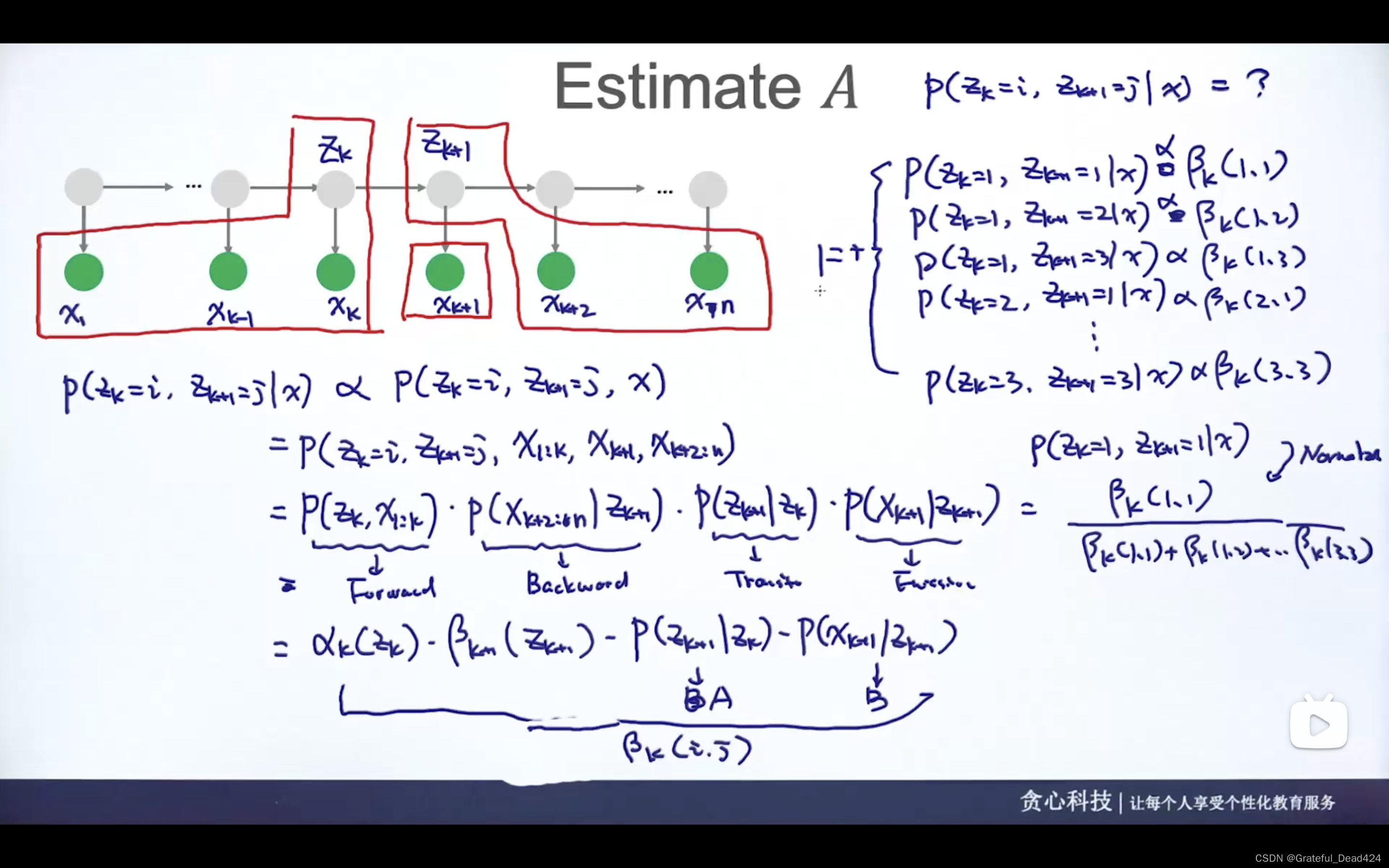


这里讨论观测、状态变量都是离散的HMM的情况
