[人工智能]TransGate: Knowledge Graph Embedding with Shared Gate Structure

题目：TransGate: Knowledge Graph Embedding with Shared Gate Structure

1 问题

目前的模型，当前的模型通过专注于从越来越复杂的特征工程中区分特定于关系的信息来改进嵌入，导致这些模型消耗大量的时间和空间，不能有效应用于现实世界大量的数据。论文中作者采用参数共享，能够学习更多的特征，减少参数避免模型更加复杂。基于Gate模式提出TransGate,利用部分Gate的思想构建模型，并对提出的模型进行重构减少参数，虽然效果比没有简化版的TransGate，要弱一些，但是性能超过了现有baseline模型，均衡参数和准确率。
目前一些模型存在的问题：

1. 参数大，模型的十分庞大，难以训练
2. 增加embedding维度去改善embedding效果
3. 由于参数过大，采用预训练避免过拟合，以减少模型同时训练的时间。

2 模型

2.1 模型图

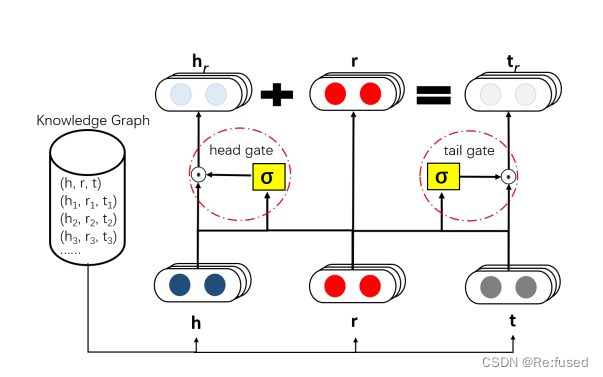
2.2 框架执行流程

1. 嵌入entity和relation到一个连续的维度相同的空间
2. 处理上图中的一个圈, TransGate对于head entity和tail entity分别设置一个Gate.
3. 对于head entity,将head embedding 和relation embedding 乘以一个Gate共享的参数${\mathbb{W}}_h$， 将其结果进行sigmoid，其实也就是相当于产生一个重置门。
4. 将实现的Gate处理之后的结果与输入相应的的head embedding 或者tail embedding相乘，采取Hadamard product的形式。
5. 最后建立类似于TransE的模型，实现打分函数。

2.3 公式

TransGate分为两个版本，其大体上差不多，只不过是在Gate参数设置方便存在差异，一个是正常版本参数量接近与ConvE，另外一个是参数精简版，分别是TransGate(fc)和TransGate(wv)。
对于向量$h,r,t\in {\mathbb{R}}^m$

2.3.1 TransGate(fc)

$h_r=h\odot \sigma (W_h?[h,r]+b_h)$
$t_r=t\odot \sigma (W_t?[t,r]+b_t)$
其中$W_h,W_t\in {\mathbb{R}}^{m\times 2m},b_t,b_h\in {\mathbb{R}}^m,\sigma$为激活函数是数据的取值范围在(0, 1)之间

2.3.2 TransGate(wv)

$h_r=h\odot \sigma (V_h\odot h+V_{rh}\odot r+b_h)$
$t_r=t\odot \sigma (V_t\odot t+V_{rt}\odot r+b_t)$
其中$V_h,V_t,V_{rh},V_{rt}\in {\mathbb{R}}^m$

2.3.3 参数对比

m作为entity embedding 维度，而n作为relation embedding维度，$N_e,N_r$分别是实体个数和关系个数。
参数的复杂度对比：
fc版本参数为$O(4m^2+2m)$
wv版本参数为$O(4m+2n)$
嵌入空间参数二者一致：
$O(N_{e}m+N_{r}n)$

2.3.4 评分函数

评分函数与TransE的评分函数是一致的，对于正确的三元组得分比错误的三元组得分低。
$f_r=||h_r+r?t_r|{|}_{L_1/L_2}$

3 损失函数

损失函数为margin-based ranking criterion,公式如下：

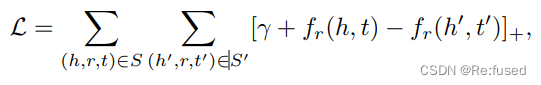
其中$[x{]}_{+}?max(0,x),\gamma >0$是margin的超参数

4 实验结果

4.1 复杂度

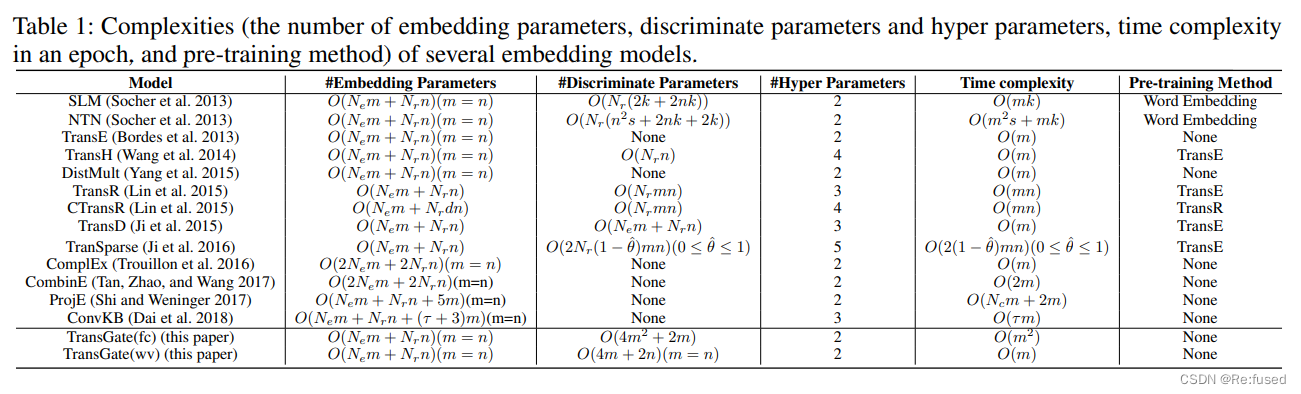
4.2 模型效果对比

对于FB15k和FB15k-237两种模型效果都比较好，但是fc版本的效果明显优于wv版本的效果，但是二者的效果都由于baseline版本的效果，但对于WN18RR数据效果就不尽人意。

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖