[人工智能]《Machine Learning Fundamentals》Class Notes -- Chapter Nine Clustering

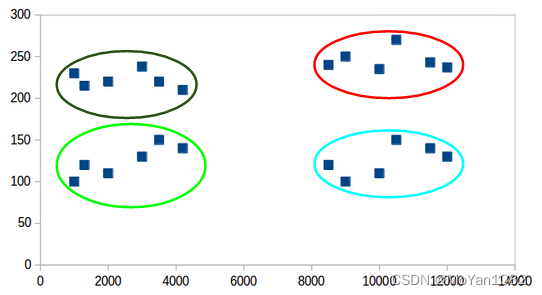
What are clustering algorithms used for?

We want to divide the data into several different types(different clusters) without labels. Data in the same cluster have some similar features for a given dataset.

We might as well define tihs similarities as distance. Therefore, our goal is to find a partition such that the intra-cluster distance is small and the inter-cluster distance is large.

Figure1：intra-cluster and inter-cluster distance

we need to determine the appropriate distance measure based on the samples. Here we will use Euclidean distance as a similarity measure.

$$Euclideandistance:\sqrt{\sum _{u=1}^n\Vert x_{iu}?x_{ju}{\Vert }^2}$$

Figure2：Clustring

The problem we need to optimize

Divide the dataset { x 1 , x 2 , . . . , x M } \{x_1,x_2,...,x_M\} {x1?,x2?,...,xM?} into disjoint sets { S 1 , S 2 , . . . , S K } \{S_1,S_2,...,S_K\} {S1?,S2?,...,SK?}. For each set $S_k$, the representative point is chosen as ${\mu }_k$.

The loss function can be defined as:
$$E(S_1,...,S_K;{\mu }_1,...,{\mu }_K)=\frac{1}{N}\sum _{m=1}^M\sum _{k=1}^K[[x_m\in S_k]]\Vert x_m?{\mu }_k{\Vert }^2$$

Therefore, our goal is to find an optimal partition that minimizes $E$.
$$\underset{S_1,...,S_K;{\mu }_1,...,{\mu }_K}{\min }E(S_1,...,S_K;{\mu }_1,...,{\mu }_K)$$

(Note: Going directly to find the optimal solution of $E$ is an NP-hard problem.)

K-Means

1. Assuming that ${\mu }_1,...,{\mu }_k$ have been determined, then for each sample $x_m$, $x_m$ can be divided into a certain cluster that minimizes ${\sum }_{k=1}^K[[x_m\in S_k]]\Vert x_m?{\mu }_k{\Vert }^2$. (The representative point ${\mu }_k$ closest to $x_m$).
2. Assuming that $S_1,...,S_K$ have been determined, then for each cluster $S_k$, we can find a certain representative point ${\mu }_k$ to minimize $E_k={\sum }_{x\in S_k}\Vert x?{\mu }_k{\Vert }^2$.
   $$\frac{d{E}_k}{d{\mu }_k}=\sum _{n_1}2(x_{n_1}?{\mu }_k)(?1)+\sum _{n_2}2({\mu }_k?x_{n_2})=2(|S_k|{\mu }_k?\sum _{x\in S_k}x)$$
   So, when ${\mu }_k=\frac{1}{|S_k|}{\sum }_{x\in S_k}x$, the derivative of $E_k$ with respect to ${\mu }_k$ is 0. (The ${\mu }_k$ also called the means vector for cluster $S_k$)
3. Steps 1 and 2 are repeated until the representative points $\mu$ no longer change.

When we do the above operations, the value of $E$ is updated to $E^{\prime }$, $E^{\prime }\le E$, and $E$ has a lower bound $E\ge 0$.
Therefore, it has been proved that the loss function must converge.
（Note: the loss function will eventually converge to a local extremum, not necessarily a global minimum.）

This also can be proved by EM(Expectation-Maximization) algorithm.

X-means

In the K-means algorithm, the value of $K$ is fixed. However, it is often difficult to choose the best $K$.

For the X-means algorithm, users can choose a range of $K$, and the X-means first runs the ordinary K-means algorithm according to the lower limit of the range. According to the value of BIC(Bayesian information criterion), the X-means algorithm determines whether to divide each cluster into two.
PDF: X-means: Extending K-means with Efficient Estimation of the Number of Clusters

Figure3: An illustration of X-means algorithm. Source: www.cs.cmu.edu

Hierarchical Clustering

Hierarchical clustering provides another idea to help users interpret the appropriate number of clusters.

Take AGNES(AGglomerative NESting) as an example:

1. Consider each sample as a cluster.
2. Merge the two clusters with the smallest distance. (inter-cluster distance)
3. Steps 1 and 2 are repeated until all clusters are merged into one single cluster including all points.

Figure4: An illustration of hierarchical clustering. Source: 🍉 Book

Users can observe the distance between clusters and choose an optimal $K$ by themselves.

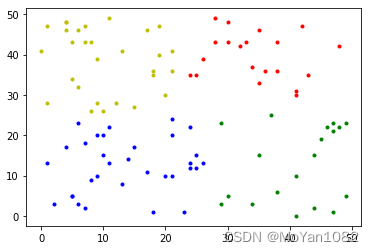
Code(K-means)

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans

data = np.random.randint(0,50,size=[100,2])
K = 4 # fix the value of K
kmeans = KMeans(n_clusters=K, random_state=0).fit(data)
subCenter = list(kmeans.labels_)

# drawing
samples = [[] for i in range(K)]
for i in range(np.shape(data)[0]):
    tmp = [data[i][0], data[i][1]]
    samples[subCenter[i]].append(tmp)
plt.plot(np.array(samples[0])[:, :1], np.array(samples[0])[:, 1:], 'b.')
plt.plot(np.array(samples[1])[:, :1], np.array(samples[1])[:, 1:], 'r.')
plt.plot(np.array(samples[2])[:, :1], np.array(samples[2])[:, 1:], 'y.')
plt.plot(np.array(samples[3])[:, :1], np.array(samples[3])[:, 1:], 'g.')
plt.show()

Figure5: The result of K-means

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖