在过去的几十年里,强大的基于核磁共振成像的方法已经被开发出来,这些方法产生了基于体素的大脑活动图和与不同情况相关的解剖变化。对于功能性或结构性MRI数据,正向推断试图确定哪些区域涉及到心理功能或大脑紊乱。正向推理的一个主要缺点是它缺乏特异性,因为它表明大脑区域的参与对被调查的过程/条件不是特定的。因此,需要一种不同的方法来确定特定的大脑激活或改变模式在多大程度上与心理功能或大脑病理相关。在本研究中,我们提出了一种名为BACON(贝叶斯因子建模)的新工具,用于对功能和结构神经成像数据进行反向推理。BACON实现了贝叶斯因子,并使用激活似然估计衍生图来获得关于特定心理功能或大脑病理特异性证据的后验概率分布。
1.简介
脑区概念是规范和临床人群脑成像研究的核心。来自神经元领域的复杂活动是认知和感觉运动功能的生理基础的形成部分。另一方面,神经元区域可能呈现不同程度的解剖变异,这取决于它们受到的病理影响。
在过去的几十年里,强大的活体核磁共振成像方法已经被开发出来;它们分别给出了不同条件和过程下的大脑结构和功能的地图。例如,功能(fMRI)图,以静止状态或与任务相关的方式生成,提供了大脑某些部分的活动和特定的心理功能之间的联系,而基于体素的形态测量法(VBM),测量脑组织局部浓度的差异,可以建立大脑结构异常和病理状况发生之间的关系。
关于功能或结构数据,前向推断试图决定哪个脑区被纳入了给定的心理功能或脑疾病。换句话说,前向推断的目的是回答这样的问题:哪些大脑区域参与了这种心理过程?或者在特定的病理中哪些是被改变的大脑区域? 在这种情况下,答案是通过频率统计程序来寻求的,例如最大似然法。然而,正向推理的主要缺点是它缺乏特异性,因为它倾向于建议涉及的区域不是特定的调查变量。例如,可以发现一个大脑区域在不同的过程中被激活,导致功能的大量重叠,如Anderson,Kinnison,和Pessoa(2013)和Cauda等人(2012)所示。类似地,神经亚群可能会被广泛的大脑障碍所损害,这大大减少了前向推断和相关图的效用。
因此,需要一种不同的方法来确定与大脑激活或改变模式相关的特定认知功能或病理,特别是回答以下问题:大脑区域(一种模式)的激活在多大程度上是特定于疼痛感知的?或者大脑区域(某种模式)的改变在多大程度上是特定病理的? 这正是基于贝叶斯定理的逆向推理分析的目的。
反向推理已经被大量的神经影像学研究采用,从Poldrack(2006)的开创性工作开始,他将反向推理应用于从BrainMap数据库的功能部分获得的元分析数据。特别是,Poldrack研究了broca’s area对语言功能的激活有多具体。此外,Cauda等人最近的一项研究指出,反向推理可以确定特定脑功能障碍引起的特定形态变化模式。
在Poldrack的工作(2006)之后的几年里,贝叶斯定理在神经成像中的应用受到了激烈的争论,主要集中在先验的选择上,这是该定理应用的一个关键方面。在Lieberman和Eisenberger(2015)发表后,正确进行逆向推理的困难已被广泛讨论,他声称前背扣带的活动对疼痛是有选择性的。这些作者的结果是基于在Neurosynth的帮助下进行的分析,这是一个免费的平台和数据库,用于mri数据的自动合成(http://www.neurosynth.org)。在评估反向推理的可行性时,需要注意的是,它不仅需要与任务或病理相关的MRI数据样本,还需要与该样本的否定相关的数据。这可以通过广泛搜索具有同行评审内容的数据库(如PubMed, PsycInfo, Web of Science, BrainMap等)来实现。
到目前为止,计算特异性估计(即关联检验)的唯一可用方法是Neurosynth。这个平台虽然很有价值,但在结构和操作数据查询的可能性方面存在一些限制。此外,Neurosynth存储了fMRI结果,但缺乏结构数据,这对于研究大脑改变的模式至关重要。进一步的限制涉及方法和统计问题。关联测试可以通过Neurosynth接口直接执行,但正确的反向推理需要对Neurosynth的核心工具进行编程。更重要的是,Neurosynth基于频率论方法,并继承了其局限性。频率主义方法除了需要大量的数据来进行一致的推理外,并没有给出假设有效性的概率,而仅仅是一个拒绝零假设的标准,这可能会导致误解。最后,用于关联测试的核是一个固定半径的球形核,因此结果映射表明每个体素在r毫米(mm)内的峰数。
为了给神经成像领域提供一种合理的逆向推理方法,本研究提出了一种新的计算工具,称为BACON (Bayes fACtor mOdeliNg),它可以对功能和结构神经成像数据进行逆向推理。BACON基于贝叶斯统计,特别是贝叶斯因子(BF),并使用GingerALE软件包生成的激活似然估计(ALE)衍生图。
值得注意的是,提出的贝叶斯方法提出了几个与频率主义方法相比的优势:(a)它不仅提供了一个二分拒绝/不拒绝的决定与零假设,但它计算的证据有利于每一个假设考虑;(b)可用于多个假设的评价;?支持感兴趣假设的数据可以不断更新(即贝叶斯更新);(d)与neurosynth不同的是,ALE使用了一个高斯核,其方差由实验中的受试者数量建模,这允许对峰值分布的变异性建模;最后,(e)该方法提供了考虑到焦点的独立激活(或改变)的最终激活(或改变)概率。
在这里,我们展示了在元分析数据分析中使用BF的基本原理和统计数据,并提出了一种不同的、改进的方法来计算神经成像数据的BF。这种方法是在一个名为BACON(贝叶斯因子建模)的新工具中实现的,该工具旨在从元分析神经成像数据计算BF值。BACON是作为插件软件(ric.uthscsa.edu/mango;多图像分析GUI),即一个具有多种分析工具的医学图像查看器。为了证明这个概念,我们使用从BrainMap中提取的功能和结构数据集来测试BACON。
因此,BACON是对BrainMap的一个重要补充,因为它提供了一种新的方法来执行基于反向推理的分析。这对于大脑疾病的研究尤其有见地,因为BACON允许区分那些被大多数大脑疾病改变的区域和那些被特定疾病特别影响的区域。更重要的是,当从时间进展的角度考虑神经病理学时,BF指数可以确定哪些脑区可能早期受到疾病的影响。
2. 方法简述
逆向推理的基础是贝叶斯定理。为了将其置于神经成像领域,让我们考虑两个假设:H0肯定某一特定状态的发生(例如,一种病理状态,如精神分裂症,或一种心理功能,如对痛苦刺激的处理),和H1肯定该状态的缺失(即否定H0)。让D成为一个大脑区域或体素激活(或结构改变)的测量。给定测量(D),特定状态实际发生的概率是多少?(H0为真?)
根据贝叶斯理论,有:
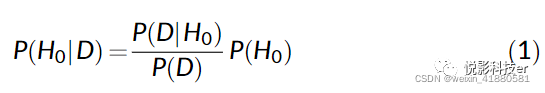
相应的:
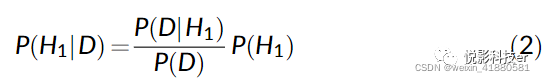
这些概率的商代表贝叶斯定理中相对信度项:
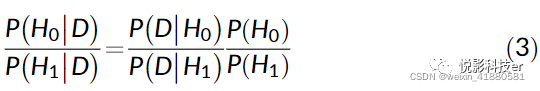
考虑先验P(H0),P(H1).如果不知道这些先验,自然地将它们考虑为相同的:

BF01表示为:

BF01给出了证据的程度:如果BF01大于1,证据支持H0,反之则反。
考虑(3)(4),BF01也可写为:

因为两个后验的和必须为1:
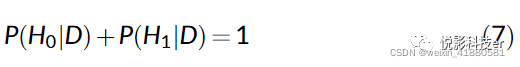
公式6写为:
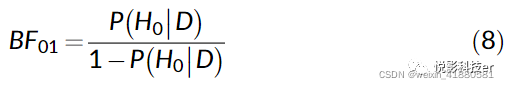
图1 为公式的图形解释:
反演8得到:
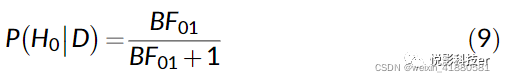
该表达式的优点是可以通过计算BF直接得到后验概率。这使得我们可以根据我们想要验证的假设来选择概率水平。
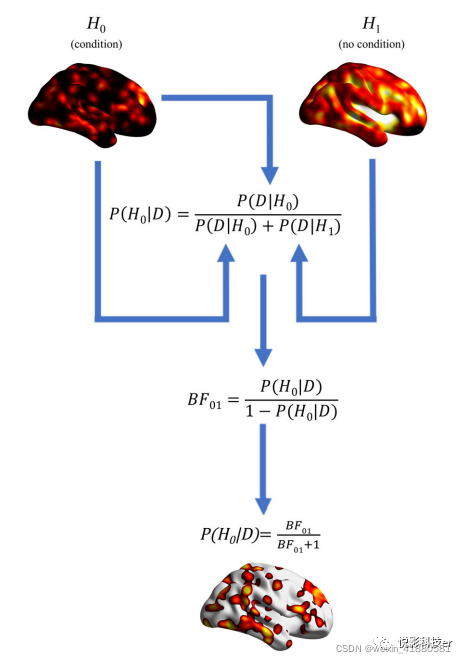
图1 公式的图形解释
BACON要求输入一对ALE派生的映射。最直接的方法是使用Sleuth软件(http://www.brainmap.org/sleuth/)在BrainMap数据库中搜索数据,然后使用Gin-gerALE(www.brainmap.org/ale;参见图2)。
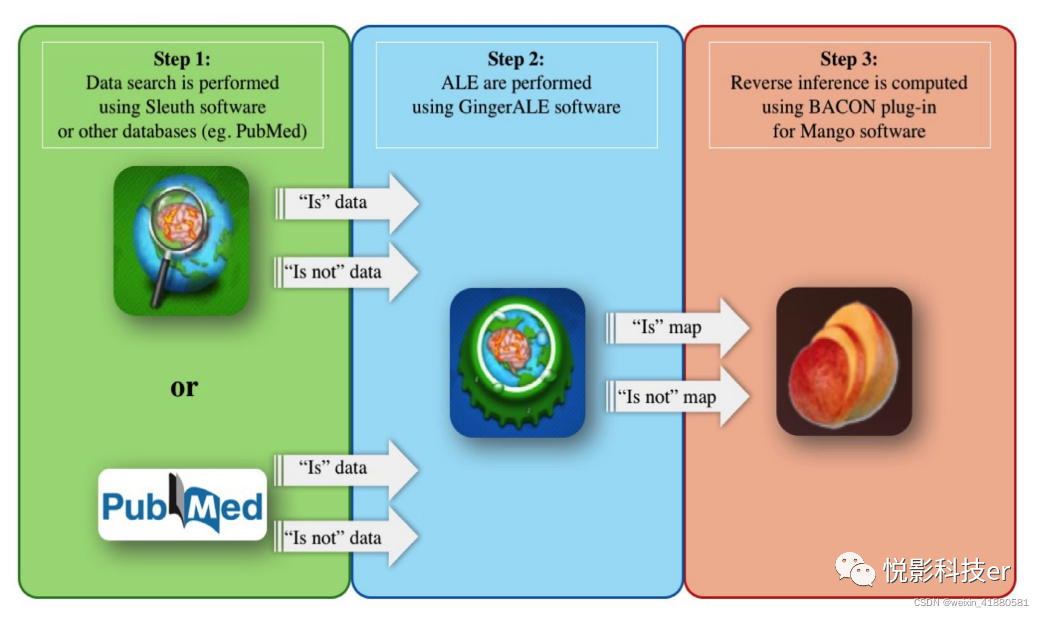
图2 用BACON插件计算特异性的流程
3. 结果
3.1 疼痛域
疼痛域的后向概率图显示:双侧岛叶(ba13)、左侧扣带回(ba24)、右侧额中下回(ba10)、双侧丘脑(右内侧背侧核和双侧腹侧核)、右侧中央后回(ba5)、右侧壳核(扁形核)、左侧颞上回(BA 22)(图3)。
将后验概率图提交到Mango行为分析插件中。不同阈值的结果不同。利用概率图阈值p=0.7,我们发现在51个行为子域中,只有7个超出了统计显著性水平。值得注意的是,躯体感觉(疼痛)子域的z值最高。使用概率图阈值p=0.8,只有躯体感觉(疼痛)和躯体感觉(其他)子域报告了显著的结果。最后,我们将Neurosynth生成的地图(即关联地图)提交给行为插件。总的来说,结果表明特异性较低相比概率地图获得BACON(参见图4)。
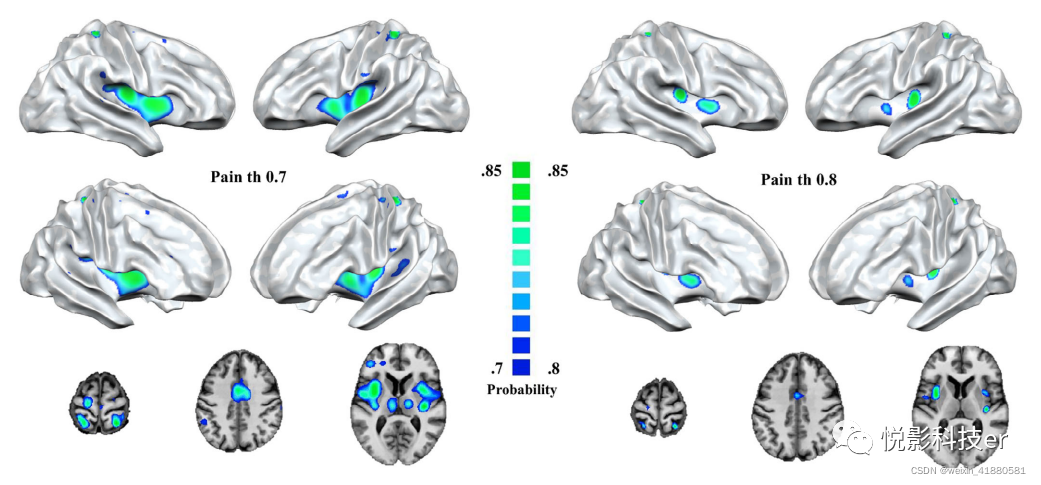
图3 不同疼痛阈值特异性的后验图
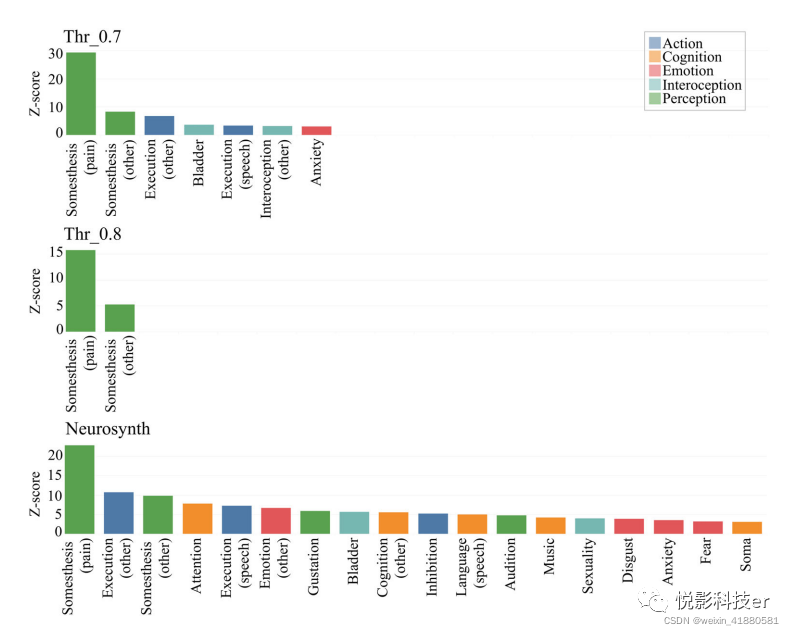
图4 比较与认知域疼痛相关的地图的行为分析结果
3.2 精神分裂症认知
SCZ的后向概率图显示了右侧颞中回(ba21)、双侧中央前回(ba6)、左侧额中回(ba10)、左侧颞上回(ba22和ba42)、双侧楔前叶(ba7)受累率(图5;不同阈值见表S6和S7)。
将sczvbm数据获得的后向概率图提交到Mango疾病分析插件中。对于使用的两个阈值(即0.7和0.8),只有SCZ超过了统计显著性水平。
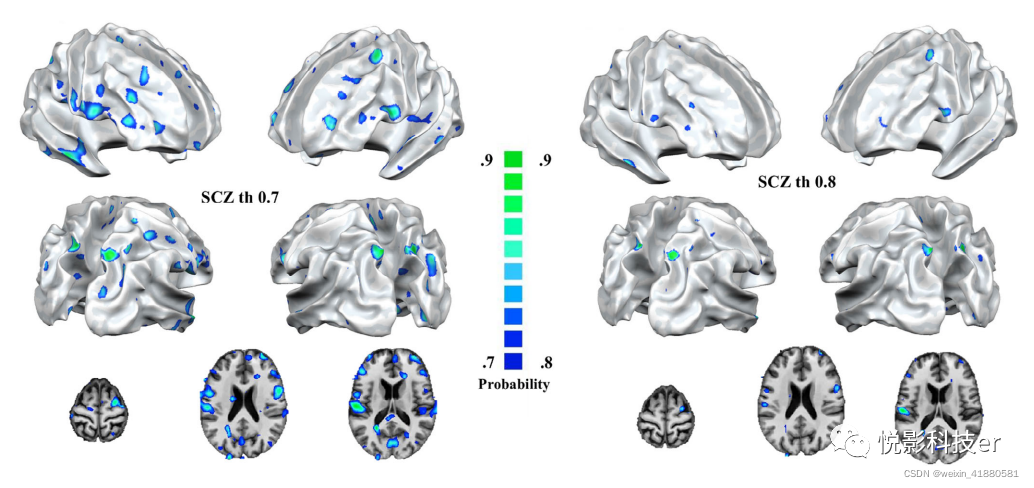
图5 SCZ不同阈值特异性后验图
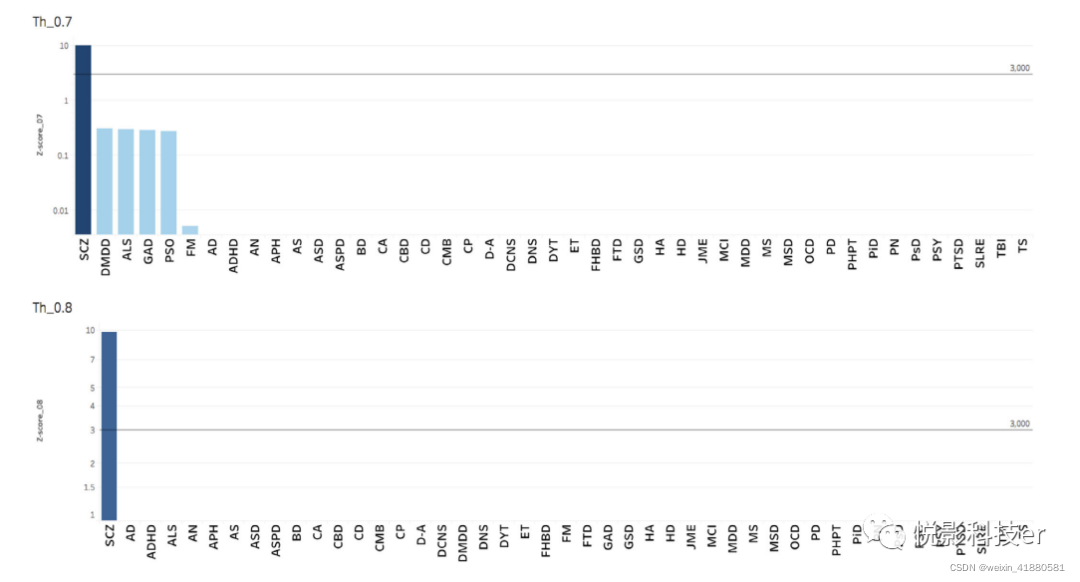
图6 精神分裂症相关图谱的行为分析结果比较
4. 讨论和结论
在本研究中,我们提出了贝叶斯定理的一种新应用,用于神经成像数据的分析,更具体地说,用于计算它们与特定过程或病理条件有关的特异性。BF的计算,在这里是专门为ALE地图进行的,可以用概率来显示结果;这反过来又导致了不同程度的特异性的概念。这种方法是在BACON中实现的,BACON是一个用户友好但功能强大的插件,它不仅可以用于brainmap元数据的管道,也可以用于其他存储同行评审的神经成像结果的数据库。行为分析证实了该工具的可靠性。事实上,输出地图的阈值为0.7(即70%的概率)与51个可能的认知区域中的7个相关,最强的是疼痛。将阈值增加到0.8将关联减少到只有两个域。在SCZ地图上进行的疾病分析也显示了证实的证据。这一结果并不明显,因为与不同精神疾病和神经退行性疾病相关的结构改变模式存在高度重叠。
值得注意的是,通过BACON得到的概率映射比那些按照典型频率主义方法构造的概率映射更不容易被误解。事实上,在贝叶斯框架中,结果直接代表了现象发生的概率。这就可以直接回答以下问题:地图上的大脑区域具体参与特定过程的可能性有多大?此外,BF比较了两个假设(H0vs.H1)是完全由观测数据条件。由于这个原因,我们有可能研究它的特异性和非特异性。相反,在更常用的基于p-value的方法中,如果原假设(H0)被拒绝,就不能对备择假设说什么。最后,用BF得到的结果不受多次比较问题的影响,因为这是频率主义方法的情况。
值得注意的是,到目前为止,基于神经影像学文献中报道的BF的分析是将数据视为二进制进行的(即,在给定的任务中,体素是活跃的还是不活跃的)。相反,这里使用的ALE方法考虑了在一系列实验中激活(或改变)体素的概率;这样就可以对激活峰的分布进行更精确的建模。更重要的是,ALE算法的使用允许正确地考虑多个结果之间的空间不确定性,以及控制由于小样本容量而导致的低功率实验可能引入的偏差。
总之,我们提出了另一种方法来调查元分析数据,其最终结果是一个后验概率图,允许以简单和直接的方式进行反向推理。BACON的使用对增进我们对大脑的理解有重大贡献,包括对大脑健康功能的理解和对大脑在病理状态发展过程中变化的理解。
参考文献:BACON: A tool for reverse inference in brain activation and alteration
