论文地址:https://arxiv.org/pdf/1808.09781.pdf
Self-Attentive Sequential Recommendation
SASRec是较早应用Self-Attention到序列推荐中的模型,目前作为序列SOTA的baseline,应用十分广泛。在工业界也是很早就大规模落地,取得的效果也是非常显著,在SASRec基础上面进行改进的工作很多,包括后面引入对比学习,加入其他side info,以及加入双向Transformer结构等等。
摘要
序列模型一般是由马尔科夫链(Markov Chain)或者循环神经网络(RNN)来处理,Markov Chain假设用户的下一个行为由最近一个或者最近几个行为产生,在稀疏数据集上面表现不错。RNN能处理较长的序列,在稠密的序列上面表现不错。基于Self-Attention的SASRec能综合两者的优点,而且性能上面比基于RNN/CNN的要好。
引言
SASRec在稀疏数据集和稠密数据集上表现都不错。基于Self-Attention机制,SASRec能关注到长距离的序列依赖,而且在稀疏数据集上面,能关注到最近的序列,另外,Self-Attention可以并行,效率较高。
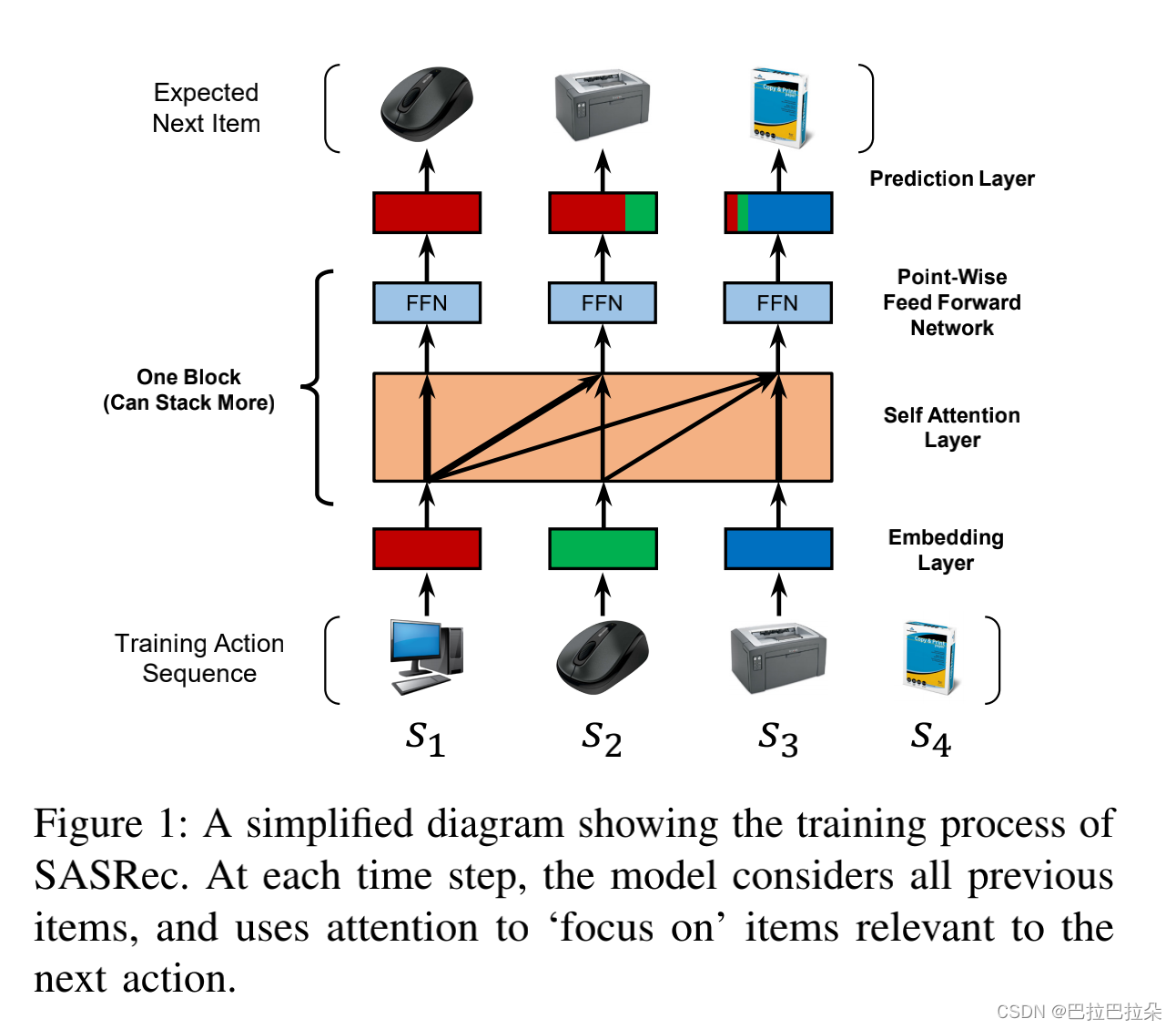
方法
符号表示
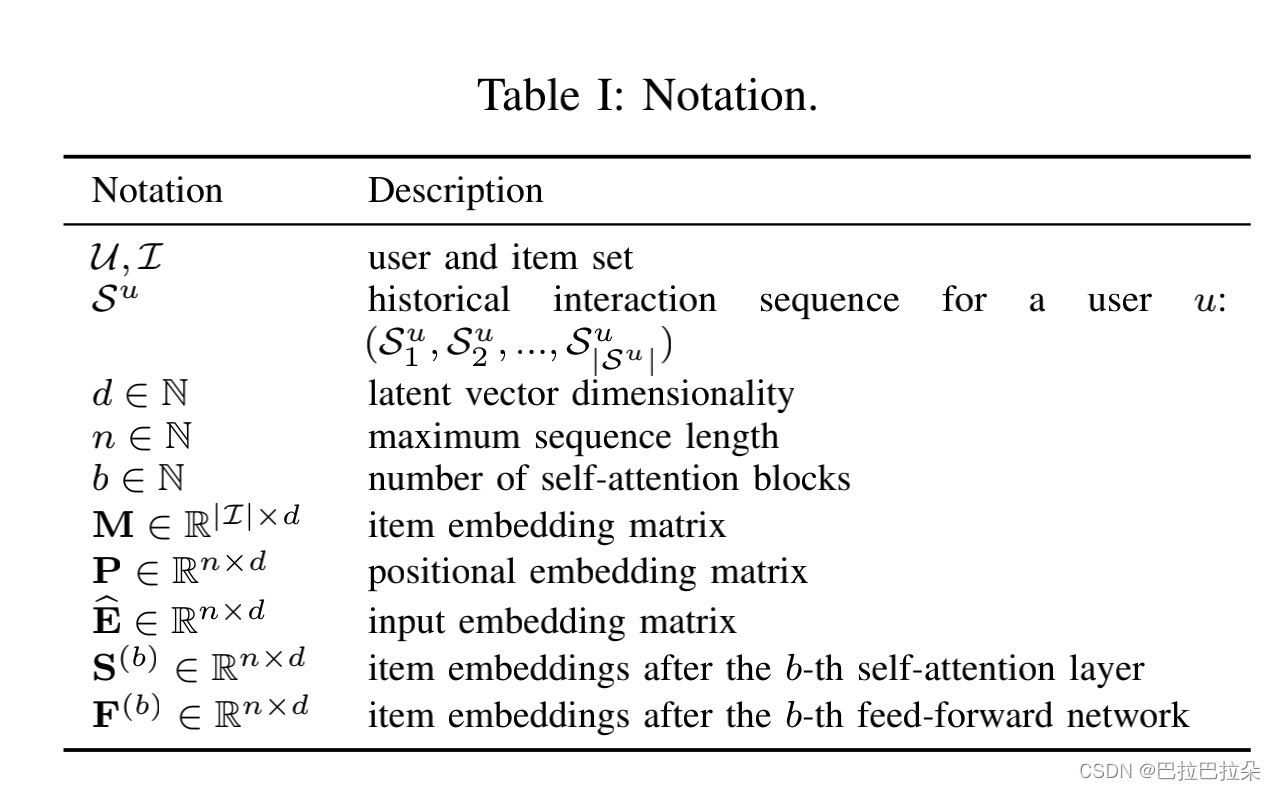
Embedding Layer
取固定长度的n个序列, s = ( s 1 , s 2 , . . . , s n ) s=(s_1,s_2,...,s_n) s=(s1?,s2?,...,sn?),如果用户序列长度不够,用padding填充,不过超过了n,就取最近的n个。item的embedding矩阵 M ∈ R ∣ I ∣ × d \mathbf{M} \in R^{\vert I \vert \times d} M∈R∣I∣×d,输入的embedding矩阵 E ∈ R n × d \mathbf{E} \in R^{n \times d} E∈Rn×d,这里 E i = M s i \mathbf{E_i} = \mathbf {M}_{s_i} Ei?=Msi??
Positional Embedding
self-attention对位置不感知,需要额外加入位置信息,引入一个待学习的位置矩阵
P
\mathbf {P}
P,论文也尝试过固定的位置embedding,效果比较差。
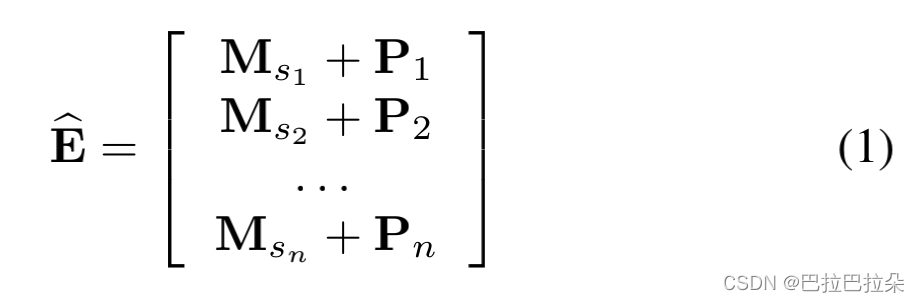
Self-Attention Block
A
t
t
e
n
t
i
o
n
(
Q
,
K
,
V
)
=
s
o
f
t
m
a
x
(
Q
K
T
d
)
V
Attention(\mathbf {Q,K,V}) = softmax(\frac {\mathbf {QK}^T}{\sqrt d}) \mathbf{V}
Attention(Q,K,V)=softmax(d?QKT?)V
Q
\mathbf Q
Q表示queries,
K
\mathbf K
K表示keys,
V
\mathbf V
V表示values(item embedding表示)。整个式子就是item向量表示的加权和。
Self-Attention Layer
S
=
S
A
(
E
^
)
=
A
t
t
e
n
i
o
n
(
E
^
W
Q
,
E
^
W
K
,
E
^
W
V
)
\mathbf S = SA(\hat {\mathbf E}) = Attenion( \hat {\mathbf E} \mathbf W^Q,\hat {\mathbf E} \mathbf W^K,\hat {\mathbf E} \mathbf W^V)
S=SA(E^)=Attenion(E^WQ,E^WK,E^WV)
即通过不同的映射投影作为Attention的输入
Causality
预测第t+1个item时仅考虑前面t个item,不能用到后面的item信息,因此需要修改 Q i \mathbf Q_i Qi?和 K j \mathbf K_j Kj?的连接当 j > i j > i j>i
Point-Wise Feed-Forward Network
F
i
=
F
F
N
(
S
i
)
=
R
e
L
U
(
S
i
W
(
1
)
+
b
(
1
)
)
W
(
2
)
+
b
(
2
)
\mathbf F_i=FFN(\mathbf S_i)=ReLU(\mathbf S_i \mathbf W^{(1)} + \mathbf b^{(1)}) \mathbf W^{(2)} + \mathbf b^{(2)}
Fi?=FFN(Si?)=ReLU(Si?W(1)+b(1))W(2)+b(2)
W
(
1
)
\mathbf W^{(1)}
W(1)和
W
(
2
)
\mathbf W^{(2)}
W(2)是
d
×
d
d \times d
d×d的矩阵
Stacking Self-Attention Blocks
第一个Self block
F
i
\mathbf F_i
Fi?基本聚合了所有item的embedding,堆叠更多的block能学习到更复杂的行为模式。对于第
b
(
b
>
1
)
b(b>1)
b(b>1)个block,定义如下
S
(
b
)
=
S
A
(
F
(
b
?
1
)
)
\mathbf S^{(b)} = SA(\mathbf F^{(b-1)})
S(b)=SA(F(b?1))
F
i
(
b
)
=
F
F
N
(
S
i
(
b
)
)
???????
i
∈
{
1
,
2
,
.
.
.
,
n
}
\mathbf F^{(b)}_i = FFN( \mathbf S^{(b)}_i ) \ \ \ \ \ \ \ i \in \{ 1,2,...,n \}
Fi(b)?=FFN(Si(b)?)???????i∈{1,2,...,n}
当网络层级较深时,容易产生几个问题
(1)模型容量增加,容易过拟合
(2)层级深梯度容易消失或者爆炸,训练过程不稳定
(3)模型参数较多,训练耗时也在增加
直接套用Transformer的解决办法,使用残差连接
Residual Connections
将低层的特征直接输入给高层,高层更容易利用低层的信息。
g
(
x
)
=
x
+
D
r
o
p
o
u
t
(
g
(
L
a
y
e
r
N
o
r
m
(
x
)
)
)
g(x) = x + Dropout(g(LayerNorm(x)))
g(x)=x+Dropout(g(LayerNorm(x)))
g表示自注意力层或者 feedforward network,先对输入x做LayerNorm,然后对g的输出做Dropout,再和原始输入x相加作为最后的输出。
Layer Normalization
Transformer里面用的是Layer Normalization,而不是Batch Normalization,主要原因是序列任务经常长短不一,而输入是固定维度,不够长的会补0,如果使用BN,会导致数据失真的比较严重,但是LN不存在这个问题,每个样本Normalization是独立的,不受其他样本的影响。
L
a
y
e
r
N
o
r
m
(
x
)
=
α
⊙
x
?
μ
σ
2
+
?
+
β
LayerNorm(x)=\alpha \odot \frac {x - \mu} { \sqrt {\sigma^2 + \epsilon}} + \beta
LayerNorm(x)=α⊙σ2+??x?μ?+β
α
\alpha
α 和
β
\beta
β是待学习的参数
Prediction Layer
堆叠了b个self-attention blocks之后,再加一个MF Layer来预测,
r
i
,
t
=
F
t
(
b
)
N
i
T
r_{i,t} = F_t^{(b)}N_i^T
ri,t?=Ft(b)?NiT?
r
i
,
t
r_{i,t}
ri,t?表示序列
(
s
1
,
s
2
,
.
.
.
,
s
t
)
(s_1,s_2,...,s_t)
(s1?,s2?,...,st?)的下一个行为item是item
i
i
i的相关性分数
N
∈
R
∣
I
∣
×
d
N \in R^{\vert I \vert \times d}
N∈R∣I∣×d 是item embedding矩阵
Shared Item Embedding
出于减少模型大小及避免过拟合的原因,使用单个item embedding矩阵
M
M
M
r
i
,
t
=
F
t
(
b
)
M
i
T
r_{i,t} = F_t^{(b)}M_i^T
ri,t?=Ft(b)?MiT?
Network Training
将每个用户的序列(
S
1
u
,
S
2
u
,
.
.
.
,
S
∣
S
u
∣
?
1
u
S_1^u,S^u_2,...,S^u_{\vert S_u \vert -1}
S1u?,S2u?,...,S∣Su?∣?1u?)从处理成一个固定长度的序列
s
=
{
s
1
,
s
2
,
.
.
.
,
s
n
}
s=\{s_1,s_2,...,s_n\}
s={s1?,s2?,...,sn?},定于
o
t
o_t
ot?表示t时刻希望的输出
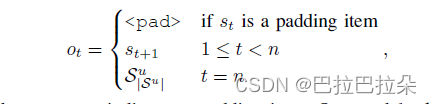
定义交叉熵损失函数如下
?
∑
S
u
∈
S
∑
t
∈
[
1
,
2
,
.
.
.
,
n
]
[
l
o
g
(
σ
(
r
o
t
,
t
)
)
+
∑
j
?
S
u
l
o
g
(
1
?
σ
(
r
j
,
t
)
)
]
-\sum_{S_u \in S} \sum_{t \in [1,2,...,n]} [ log(\sigma(r_{o_t,t})) + \sum_{j \notin S_u} log(1 - \sigma(r_{j,t})) ]
?Su?∈S∑?t∈[1,2,...,n]∑?[log(σ(rot?,t?))+j∈/?Su?∑?log(1?σ(rj,t?))]
Complexity Analysis
Space Complexity:
O
(
∣
I
∣
d
+
n
d
+
d
2
)
O(\vert I \vert d + nd + d2)
O(∣I∣d+nd+d2)
Time Complexity:主要是self-attention和the feed forward network的计算
O
(
n
2
d
+
n
d
2
)
O(n^2d + nd^2)
O(n2d+nd2)
但是attention是能够并行计算的,实际这里耗时可以接受
实验
实验回答4个问题:
RQ1:SASRec是不是比包括CNN/RNN的方法好?
RQ2:SASRec不同组件的影响如何?
RQ3:SASRec训练性能如何?
RQ4:attention的权重是否能学到item属性或者位置的有意义的模式?
数据集
3个应用的4个数据集,数据的平台、领域、稀疏性差异显著
Amazon:从Amazon.com.产生的数据集,分成2个数据集‘’Beauty,’ and ‘Games’
Steam:大型在线视频游戏分发平台
MovieLens:很多推荐系统的基线
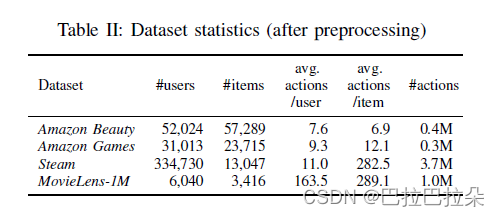
对数据进行处理,对行为序列按照时间排序,去掉序列长度不超过5的用户。按照最近的时间顺序将用户序列分成3部分,一部分测试,一部分验证,其他的训练。
对比方法
PopRec:流行度推荐,就是热门推荐
Bayesian Personalized Ranking (BPR):
基于一阶马尔科夫链的模型
Factorized Markov Chains (FMC):将item矩阵分解为2个embedding,依靠最近访问的item来推荐
Factorized Personalized Markov Chains (FPMC):结合矩阵分解和一阶马尔科夫链
Translation-based Recommendation (TransRec):每个用户转换成embedding
基于深度学习的模型
GRU4Rec:使用RNN的序列推荐模型
GRU4Rec
+
^+
+:GRU4Rec,的增强版,使用了不同的loss函数和采用策略
Convolutional Sequence Embeddings (Caser):基于CNN的高阶马尔科夫链
为公平起见, 向量维度 d d d考虑 { 10 , 20 , 30 , 40 , 50 } \{10,20,30,40,50 \} {10,20,30,40,50} ,正则参数 l 2 l_2 l2?考虑 { 0.0001 , 0.001 , 0.01 , 0.1 , 1 } \{ 0.0001,0.001,0.01,0.1,1 \} {0.0001,0.001,0.01,0.1,1}在验证集中找到表现最好的参数
实现细节
使用的self-attention block数目为2( b = 2 b=2 b=2),使用可学习的位置embedding,优化器是Adam,学习率为0.001,batch_size为128,dropout比例对于MovieLens-1M是0.2,其他是0.5,序列长度MovieLens-1M设置的是200,其他的设置的是50
评估指标
Hit Rate@10和NDCG@10
Hit Rate@10 下一个item在最相似的top10的比例
推荐结果
结果如下表,回答RQ1
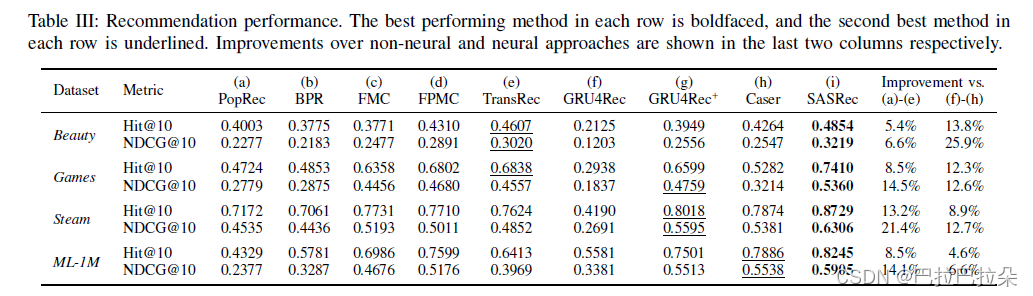
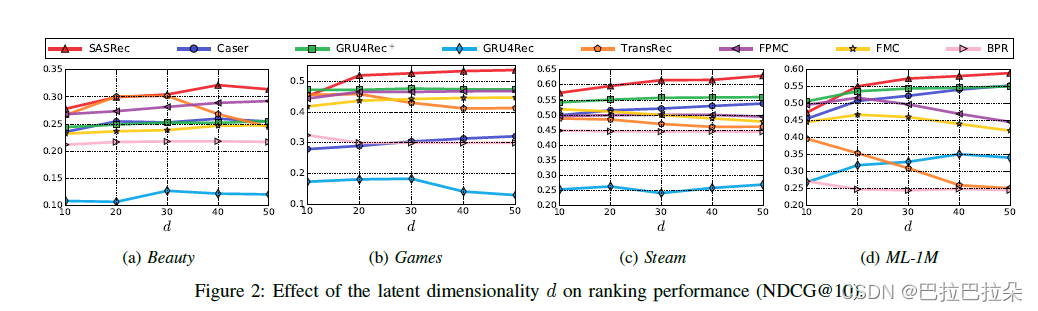
实验了超参数,embedding维度
d
d
d在
d
>
=
40
d >= 40
d>=40在所有数据集上都表现最好
拆解分析
回答RQ2:,SASRec不同的组件如何影响
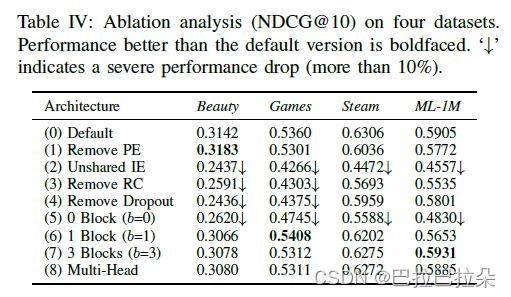
(1)Remove PE (Positional Embedding):即去掉了序列的属性特性,对于稀疏数据集可能合适,稠密的数据集就比较糟糕了
(2)Unshared IE (Item Embedding):不共享item embedding效果较差
(3)Remove RC (Residual Connections):效果显著下降,可能是低层的信息比较难进入到最后一层
(4)Remove Dropout:去掉dropout效果变差,过拟合导致
(5)-(7)0个self-attention block非常差,仅依靠最后一个item
(8)Multi-head:Transformer里面使用了多头注意力有效,但是SASRec场景效果较差,可能是因为embedding维度较小(Transformer的纬度是512)
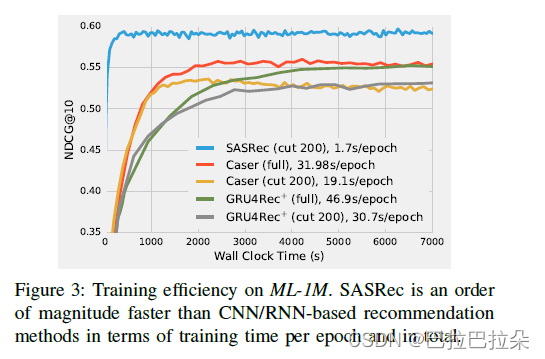
训练性能
从2个 维度评估,一个是训练速度(训练一个epoch需要的时间),另一个是训练收敛需要的时间,所有实验使用了单个GTX-1080 Ti GPU
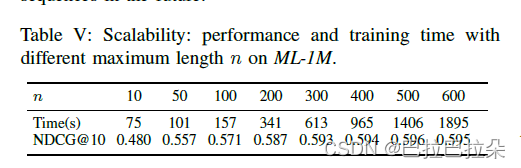
序列长度n的耗时
Visualizing Attention Weights
回答RQ4:attention 权重是否学到了有意义的模式
Attention on Positions:
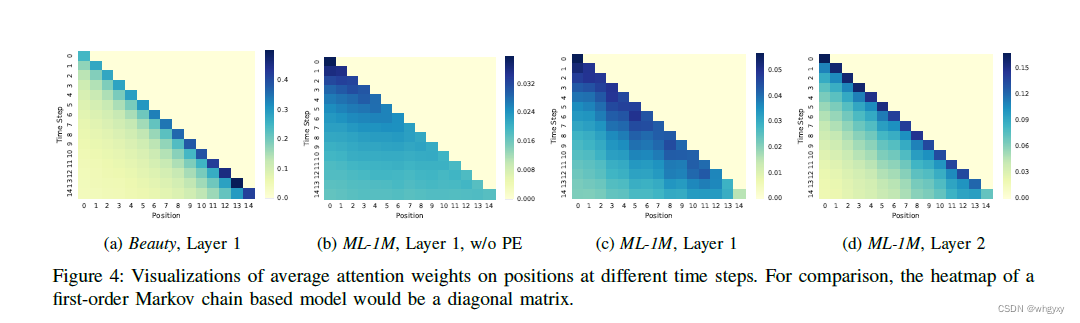
(a)vs (c):稀疏数据集Beauty上面attention权重显示更关注最近的item,稠密数据集ML-1M上面则对最近的item关注的表较少。也就是说模型能自适应的去处理不同的数据集。
(b)vs(c):显示是否使用position embedding的影响,没有位置embedding,attention权重对于每个item几乎是均匀分布的,有位置embedding的模型对于位置比较敏感,对相应位置的item关注度(权重)更高。
(c)vs(d)不同层的self attention block里面的区别,更高层的更关注相应位置的item,可能是第一层考虑了所有的item,后面的层只需要更关注相应位置的item。
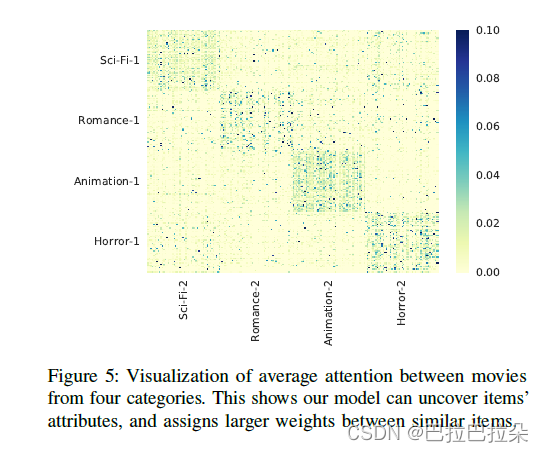
Attention Between Items:
从数据集中随机抽取2个集合,item的类目分属4种,从热力图上看到相同类目的item聚集在一起,说明模型能够根据item的属性找到相似的item。