A. Epipolar geometry and triangulation
The epipolar geometry mainly adopts the feature point method, such as SIFT, SURF and ORB, etc. to obtain the feature points corresponding to two frames of images. As shown in Figure 1, let the first image be 
? and the second image be?
? 。?
?
Fig.1 Schematic diagram of epipolar geometry and triangulation
The projections of a point?
? n three-dimensional space under two images from different perspectives are ?
?，
? . The camera coordinate system when the first frame of image is captured when the camera is turned on is pre-defined as the world coordinate system, then the projection equations of the two images are:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??(1)
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(2)
Because the scene in the three-dimensional space loses the dimension of depth in the process of projecting it to the image plane, the depth information cannot be obtained by only one image, so the normalized plane is used for calculation. The normalization plane is the plane that normalizes all the depths. It can be regarded as a plane with a depth of 1 in front of the camera imaging plane. The coordinates of the normalization plane of the two images are?
?,?
? . The transformation relationship between the normalized plane and the pixel coordinates is:
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (3)
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (4)
Integrating formula (1) to formula (3), can get:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(5)
On the basis of the above formula, the antisymmetric matrix of the translation matrix?
? can be left-multiplied on both sides at the same time, we can get:
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(6)
On the basis of the above formula, left-multiplying both sides by
? , can get:
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(7)
Let
? (E?is called the essential matrix), then there are:
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(8)
where?
?，
? . Its expanded form is:
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(9)
It can be seen that?
? can be calculated through 8 pairs of feature points. Through matrix decomposition, the rotation and translation matrices can be obtained.
After having the rotation and translation matrix, the depth of the three-dimensional space point?
? under different image viewing angles can be obtained by using equations (1) and (2), and this process is called triangulation.
B. Direct method
As shown in FIG. 2 , there are any point?
? in the three-dimensional space and two related cameras at different times and different viewing angles. The coordinates of?
? in the world coordinate system are?
? 。The pixel coordinates of the point????????
? projected to the cameras at two different times are????????
,?
? ，where????????
?,?
? is in the form of non-homogeneous coordinates, the purpose is to solve the relative transformation of the two cameras at different times, that is, rotation and translation. Taking the camera coordinate system of the first camera as a reference, suppose the transformation matrix of the cameras at two different times is??
? ，and its Lie algebra is in the form of ??
? . Two cameras at different times are the same camera and have the same internal parameter?
?.
?
Figure 2 Schematic diagram of the direct method
The complete projection equation is:
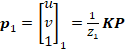? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(10)
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(11)
Where????????
? is the depth of the 3D point?
? ，
? is the depth of the 3D point????????
? in the second camera coordinate system, which is the third coordinate value of?
? . Since????????
? can only be multiplied by homogeneous coordinates, the first three elements must be taken out.
Since there is no feature matching in the direct method, it is impossible to know which 
and?
correspond to the same point. The idea of the direct method is to find the position of?
according to the estimated value of the current camera pose. But if the camera pose is not good enough, the appearance of 
?will be significantly different from ?
. Therefore, in order to reduce this difference, the pose of the camera is optimized to find?
that is more similar to?
. It is calculated by solving the optimization problem of photometric error in the form:
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(12)
where?
? is a scalar, and the optimization objective is the two-norm of the error:
?
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(13)
The direct method assumes that the grayscale of a spatial point is unchanged under various viewing angles. If there are N spatial points?
, then the whole camera pose estimation problem becomes:
? ，
?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(14)
The variable to be optimized is the camera pose 
, and this optimization problem needs to be solved by analyzing their derivative relationship. Therefore, a perturbation model on Lie algebras is used. Multiply ?
by a small perturbation?
??to the left, we get:
?? ? (15)
Abbreviated as?
? or?
? 。
Here?
is the coordinate of 
?in the second camera coordinate system after perturbation, and?
is its pixel coordinate. Using the first-order Taylor expansion, we have:
? ? ??(16)
It can be seen from equation (16) that the first derivative is divided into three terms due to the chain rule, and these three terms can be calculated separately.?
In the above derivation, 
is a point in space with a known location. With an RGB-D camera, any pixel can be back-projected into 3D space and then projected into the next image. If in a monocular camera, the uncertainty caused by the depth of needs to be considered. According to the source of ?, direct methods can be divided into three categories: 1.? comes from sparse key points called sparse direct methods. Usually hundreds to thousands of keypoints are used, assuming that the surrounding pixels are also unchanged. This sparse direct method does not have to compute descriptors and uses only hundreds of pixels, so it is the fastest, but only computes sparse reconstructions. 2.? comes from some pixels. You can consider only using pixels with gradients, and discarding the places where the pixel gradients are not obvious. This is called a semi-dense direct method, and a semi-dense structure can be reconstructed. 3.? is all pixels, which is called dense direct method. Dense reconstruction needs to calculate all pixels (generally hundreds of thousands to millions), so most of them cannot be calculated in real time on existing CPUs and require GPU acceleration. Reconstruction from sparse to dense can be computed using the direct method. Their computational load is gradually increasing. The sparse method can solve the camera pose quickly, while the dense method can build a complete map.
C. PnP
The projection process of an image is a process in which a three-dimensional point in space corresponds to a two-dimensional point in the image. If these two points are known and they are known to be corresponding, PnP can be used to calculate the camera pose.
According to the camera and image model, the world coordinate system to the pixel coordinate system needs to go through the camera's external parameters and internal parameters. The external parameter of the camera is the transformation matrix 
, which can be specifically expressed as 
? , where 
? is the rotation matrix and ? 
is the displacement vector. Positioning is to solve the problem of how much the camera rotates and translates in the world coordinate system, that is, solve 
. The world coordinate system is represented by? 
, and the camera coordinate system is represented by 
, then the transformation relationship between the world coordinate system and the camera coordinate is 
. The coordinates on the camera normalization plane are represented by 
, and the camera coordinate system to the normalization plane needs the camera's internal parameters 
?. Then there is the corresponding mathematical relationship:
???????? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(17)
According to formula (17), the coordinates?
on the normalized plane are known, and the initial value of?
is obtained by solving the linear equation system, and then the optimal transformation matrix?
is obtained by iterative nonlinear least squares method. The specific form is, consider a three-dimensional space point ?
, whose homogeneous coordinates are?
? . Point ?
corresponds to the point 
?of the homogeneous coordinates of the normalized plane. The pose of the camera is unknown. Define the augmented matrix? XXX
as a 3×4 matrix that contains rotation and translation information. Its expanded form is listed as follows:
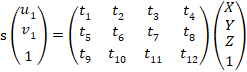?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (18)
The scale information?
of the marked point can be obtained by using the depth map from the lidar or RGB-D camera, the world coordinate of the marked point ?
is known, and the corresponding point 
on the normalized plane is known. 
is a 3×4 matrix with a total of 12 dimensions. Therefore, the linear solution of the transformation matrix is realized through six pairs of matching points. When there are more than six pairs of matching points, the method of singular value decomposition is used to obtain the least squares solution to the overdetermined equation.
D. 3D Mapping
After the pose of the image and the depth of the image are known, the pixels in the image can be restored to the spatial coordinate system. If there is a series of images, 3D reconstruction can be done by back-projecting the pixels in each image into 3D space. Since the depth information of the image plays a decisive role in the projected model, the resolution of the 3D reconstruction depends on the resolution of the image depth. Therefore, according to the density of the image depth, it can be divided into sparse 3D reconstruction, semi-dense 3D reconstruction and dense 3D reconstruction. As shown in Figure 3, sparse 3D reconstruction can only reconstruct some key points in the image, semi-dense reconstruction can reconstruct most of the information, and dense reconstruction can restore dense 3D scenes.
?
Figure 3 Reconstruction result intent [19]
Epipolar geometry and triangulation can only get sparse points in the image and therefore can only be used for sparse 3D reconstruction. PnP is mainly a localization method for RGB-D cameras, so dense 3D reconstruction can be performed through the dense depth values collected by RGB-D cameras. The direct method can usually obtain semi-dense image depth, so it is mostly used for semi-dense 3D reconstruction. There are many forms of representation of 3D reconstruction, among which the reconstruction is mostly in the form of point cloud, mesh and surface element, and its form is shown in Figure 4.
?
Figure 4 Different forms of 3D reconstruction
