学习资料参考:
张平.《OpenCV算法精解:基于Python与C++》.[Z].北京.电子工业出版社.2017.
Sobel边缘检测
sobel算子及其分离性
该算子由两部分组成:
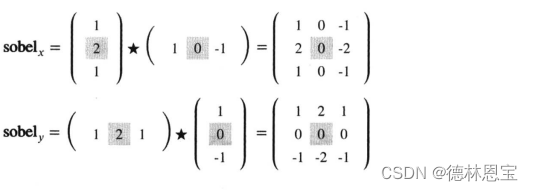
sobel算子是在一个坐标轴上进行非归一化的高斯平滑,在另一个坐标轴方向上进行差分处理。n*n的sobel算子由平滑算子和差分算子full卷积而成,其中n为奇数。
如5阶的非归一化的高斯平滑算子为

该平滑算子的中的数值从左到右其实为 4 = n - 1 = 5 - 1的二项式指数的展开系数。
而与该算子对应的差分算子为
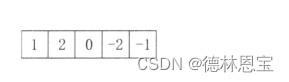
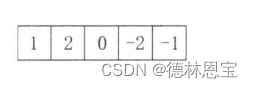
该差分算子的数值从左到右其实为,令3 = n - 2 = 5 - 2 的二项式展开系数,即
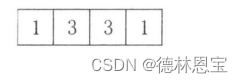
然后两侧补0,
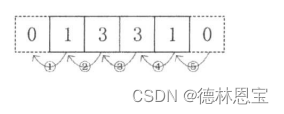
接着进行后向差分即可。
而构建sobel算子满足的普遍性的规律满足以下总结:
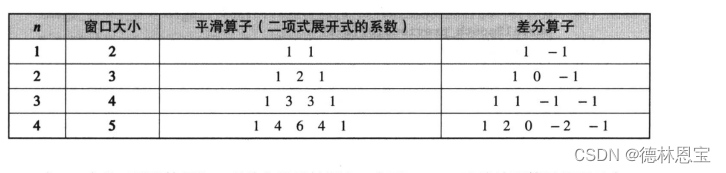
python实现
import math
from scipy import signal
import numpy as np
import cv2
# 计算平滑算子
def pascalSmooth(n):
pascalSmooth = np.zeros((1, n), np.float32)
for i in range(n):
pascalSmooth[0][i] = math.factorial(n - 1) / (math.factorial(i) * math.factorial(n - 1 - i))
return pascalSmooth
# 计算差分算子
def pascalDiff(n):
pascalDiff = np.zeros((1, n), np.float32)
pascalSmooth_previous = pascalSmooth(n - 1)
for i in range(n):
if i == 0:
pascalDiff[0][i] = pascalSmooth_previous[0][i]
elif i == n - 1:
pascalDiff[0][i] = -pascalSmooth_previous[0][i - 1]
else:
pascalDiff[0][i] = pascalSmooth_previous[0][i] - pascalSmooth_previous[0][i - 1]
return pascalDiff
# 基于前两个函数构建x轴与y轴的算子
def getSobelKernel(n):
pascalSmoothKernel = pascalSmooth(n)
pascalDiffKernel = pascalDiff(n)
# 水平方向的卷积核
sobel_kernel_x = signal.convolve2d(pascalSmoothKernel.transpose(), pascalDiffKernel, mode='full')
# 垂直方向的卷积核
sobel_kernel_y = signal.convolve2d(pascalSmoothKernel, pascalDiffKernel.transpose(), mode='full')
return sobel_kernel_x, sobel_kernel_y
# 图像与算子进行卷积
def sobel(image, n):
rows, cols = image.shape
# 得到平滑算子和差分算子
pascalSmoothKernel = pascalSmooth(n)
pascalDiffKernel = pascalDiff(n)
# 水平方向上的卷积
imgae_sobel_x = signal.convolve2d(image, pascalSmoothKernel.transpose(), mode='same')
imgae_sobel_x = signal.convolve2d(imgae_sobel_x, pascalDiffKernel, mode='same')
# 垂直方向的卷积
image_sobel_y = signal.convolve2d(image, pascalSmoothKernel, mode='same')
image_sobel_y = signal.convolve2d(image_sobel_y, pascalDiffKernel.transpose(), mode='same')
return imgae_sobel_x, image_sobel_y
if __name__ == '__main__':
image = cv2.imread(r"C:\Users\1\Pictures\test1.jpg", 0)
image_sobel_x, image_sobel_y = sobel(image, 7)
edge = np.sqrt(np.power(image_sobel_x, 2.0) + np.power(image_sobel_y, 2.0))
edge = edge / np.max(edge)
edge = np.power(edge, 1)
edge *= 255
edge = edge.astype(np.uint8)
cv2.imshow("image", image)
cv2.imshow("edge", edge)
cv2.waitKey(0)
cv2.destroyAllWindows()
运行结果

scharr边缘检测
scharr算子
该算子与Prewitt边缘检测算子和3阶的sobel边缘检测算子类似,由两个卷积核(不可分离)组成:
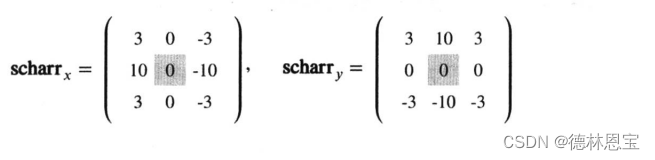
python实现
def scharr(I, _boundary='symm'):
# I与scharr_x的same卷积
scharr_x = np.array([[3, 0, -3], [10, 0, -10], [3, 0, -3]], np.float32)
I_x = signal.convolve2d(I, scharr_x, mode='same', boundary='symm')
# I与scharr_y的same卷积
scharr_y = np.array([[3, 10, 3], [0, 0, 0], [-3, -10, -3]], np.float32)
I_y = signal.convolve2d(I, scharr_y, mode='same', boundary='symm')
return I_x, I_y
kirsch、Robinson边缘检测
kirsch算子由8个卷积核组成:
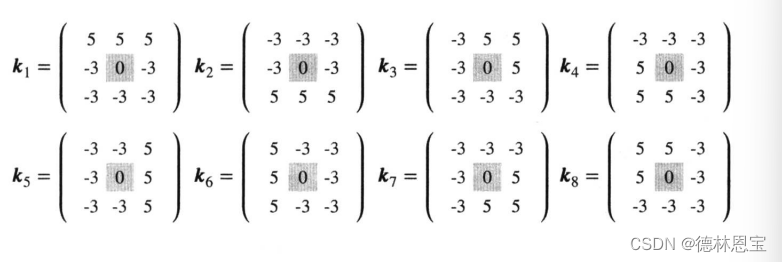
图像与每一个核进行卷积,然后取绝对值作为对应方向上的边缘强度的量化。对8个卷积的结果取绝对值,然后再对应值位置取最大值作为最后输出的边缘强度。
Robinson算子也是由8个卷积核组成:
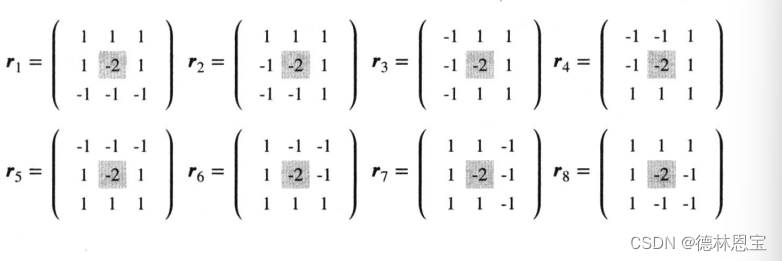
原理与kirsch算子类似。
