A New Bio-Inspired Optimization Algorithm for Solving Optimization Algorithm
参考文献:
M. Dehghani, ?. Hubálovsky and P. Trojovsky, “Tasmanian Devil Optimization: A New Bio-Inspired Optimization Algorithm for Solving Optimization Algorithm,” in IEEE Access, vol. 10, pp. 19599-19620, 2022, doi: 10.1109/ACCESS.2022.3151641.
如有侵权,联系删除
简介
???????????
??袋獾是一种食肉有袋类野生动物属于Dasyuridae科的动物,袋獾是机会主义者动物,虽然它们能捕猎,但它们也吃东西如果存在腐肉[41]。袋獾有两种策略喂养。在第一种策略中,如果袋獾找到一个它以腐肉为食。在第二种策略中,它捕食通过攻击猎物。TDO算法设计来源
原理
初始化
X
=
[
X
1
?
X
i
?
X
N
]
N
×
m
=
[
x
1
,
1
?
x
1
,
j
?
x
1
,
m
?
?
?
?
x
i
,
1
?
x
i
,
j
?
x
i
,
m
?
?
?
?
x
N
,
1
?
x
N
,
j
?
x
N
,
m
]
N
×
m
X=\left[\begin{array}{c} X_{1} \\ \vdots \\ X_{i} \\ \vdots \\ X_{N} \end{array}\right]_{N \times m}=\left[\begin{array}{ccccc} x_{1,1} & \cdots & x_{1, j} & \cdots & x_{1, m} \\ \vdots & \ddots & \vdots & & \vdots \\ x_{i, 1} & \cdots & x_{i, j} & \cdots & x_{i, m} \\ \vdots & & \vdots & \ddots & \vdots \\ x_{N, 1} & \cdots & x_{N, j} & \cdots & x_{N, m} \end{array}\right]_{N \times m}
X=?????????X1??Xi??XN???????????N×m?=?????????x1,1??xi,1??xN,1???????x1,j??xi,j??xN,j???????x1,m??xi,m??xN,m???????????N×m?
F
=
[
F
1
?
F
i
?
F
N
]
N
×
1
=
[
F
(
X
1
)
?
F
(
X
i
)
?
F
(
X
N
)
]
N
×
1
F=\left[\begin{array}{c} F_{1} \\ \vdots \\ F_{i} \\ \vdots \\ F_{N} \end{array}\right]_{N \times 1}=\left[\begin{array}{c} F\left(X_{1}\right) \\ \vdots \\ F\left(X_{i}\right) \\ \vdots \\ F\left(X_{N}\right) \end{array}\right]_{N \times 1}
F=?????????F1??Fi??FN???????????N×1?=?????????F(X1?)?F(Xi?)?F(XN?)??????????N×1?
位置更新方式
在TDO每次迭代过程中,更新方式假定选择这两种策略的概率等于百分之50
策略一:通过吃腐肉进食
C
i
=
X
k
,
i
=
1
,
2
,
…
,
N
,
k
∈
{
1
,
2
,
…
,
N
∣
k
≠
i
}
C_{i}=X_{k}, \quad i=1,2, \ldots, N, k \in\{1,2, \ldots, N \mid k \neq i\}
Ci?=Xk?,i=1,2,…,N,k∈{1,2,…,N∣k?=i}
x
i
,
j
n
e
w
,
S
1
=
{
x
i
,
j
+
r
?
(
c
i
,
j
?
I
?
x
i
,
j
)
,
F
C
i
<
F
i
;
x
i
,
j
+
r
?
(
x
i
,
j
?
c
i
,
j
)
,
?otherwise?
,
X
i
=
{
X
i
n
e
w
,
S
1
,
F
i
n
e
w
,
S
1
<
F
i
X
i
,
?otherwise?
,
\begin{aligned} x_{i, j}^{n e w, S 1} &= \begin{cases}x_{i, j}+r \cdot\left(c_{i, j}-I \cdot x_{i, j}\right), & F_{C_{i}}<F_{i} ; \\ x_{i, j}+r \cdot\left(x_{i, j}-c_{i, j}\right), & \text { otherwise },\end{cases} \\ X_{i} &= \begin{cases}X_{i}^{n e w, S 1}, & F_{i}^{n e w, S 1}<F_{i} \\ X_{i}, & \text { otherwise },\end{cases} \end{aligned}
xi,jnew,S1?Xi??={xi,j?+r?(ci,j??I?xi,j?),xi,j?+r?(xi,j??ci,j?),?FCi??<Fi?;?otherwise?,?={Xinew,S1?,Xi?,?Finew,S1?<Fi??otherwise?,??
具体参数设置请参照原文
策略二:通过吃猎物进食
P
i
=
X
k
,
i
=
1
,
2
,
…
,
N
,
k
∈
{
1
,
2
,
…
,
N
∣
k
∣
=
i
}
P_{i}=X_{k}, \quad i=1,2, \ldots, N, k \in\{1,2, \ldots, N|k|=i\}
Pi?=Xk?,i=1,2,…,N,k∈{1,2,…,N∣k∣=i}
x
i
,
j
n
e
w
,
S
2
=
{
x
i
,
j
+
r
?
(
p
i
,
j
?
I
?
x
i
,
j
)
,
F
P
i
<
F
i
,
x
i
,
j
+
r
?
(
x
i
,
j
?
p
i
,
j
)
,
?otherwise?
,
X
i
=
{
X
i
n
e
w
,
S
2
,
F
i
new?
,
S
2
<
F
i
;
X
i
,
?otherwise?
,
\begin{aligned} x_{i, j}^{n e w, S 2} &= \begin{cases}x_{i, j}+r \cdot\left(p_{i, j}-I \cdot x_{i, j}\right), & F_{P_{i}}<F_{i}, \\ x_{i, j}+r \cdot\left(x_{i, j}-p_{i, j}\right), & \text { otherwise },\end{cases} \\ X_{i} &= \begin{cases}X_{i}^{n e w, S 2}, & F_{i}^{\text {new }, S 2}<F_{i} ; \\ X_{i}, & \text { otherwise },\end{cases} \end{aligned}
xi,jnew,S2?Xi??={xi,j?+r?(pi,j??I?xi,j?),xi,j?+r?(xi,j??pi,j?),?FPi??<Fi?,?otherwise?,?={Xinew,S2?,Xi?,?Finew?,S2?<Fi?;?otherwise?,??
R
=
0.01
(
1
?
t
T
)
,
x
i
,
j
new?
=
x
i
,
j
+
(
2
r
?
1
)
?
R
?
x
i
,
j
,
X
i
=
{
X
i
new?
,
F
i
new?
<
F
i
X
i
,
?otherwise?
,
\begin{aligned} R &=0.01\left(1-\frac{t}{T}\right), \\ x_{i, j}^{\text {new }} &=x_{i, j}+(2 r-1) \cdot R \cdot x_{i, j}, \\ X_{i} &= \begin{cases}X_{i}^{\text {new }}, & F_{i}^{\text {new }}<F_{i} \\ X_{i}, & \text { otherwise },\end{cases} \end{aligned}
Rxi,jnew??Xi??=0.01(1?Tt?),=xi,j?+(2r?1)?R?xi,j?,={Xinew??,Xi?,?Finew??<Fi??otherwise?,??
具体参数设置请参照原文
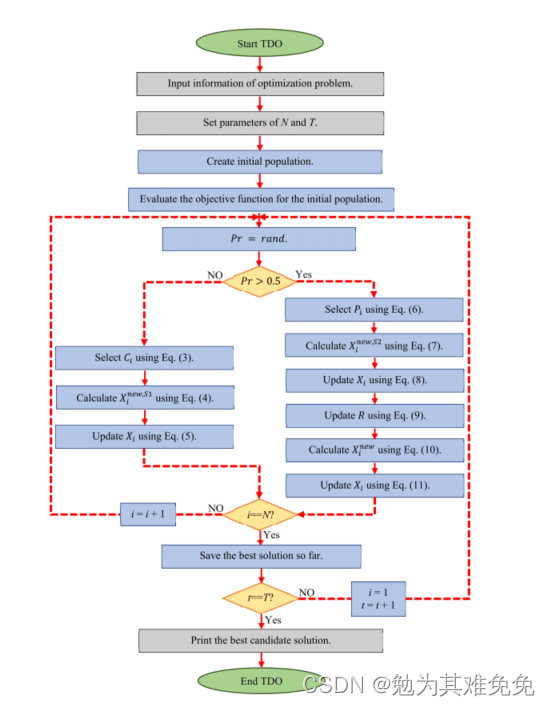
流程图
???????????
伪代码
?????????????
测试及结果分析
单峰、多峰、固定维数各一个。
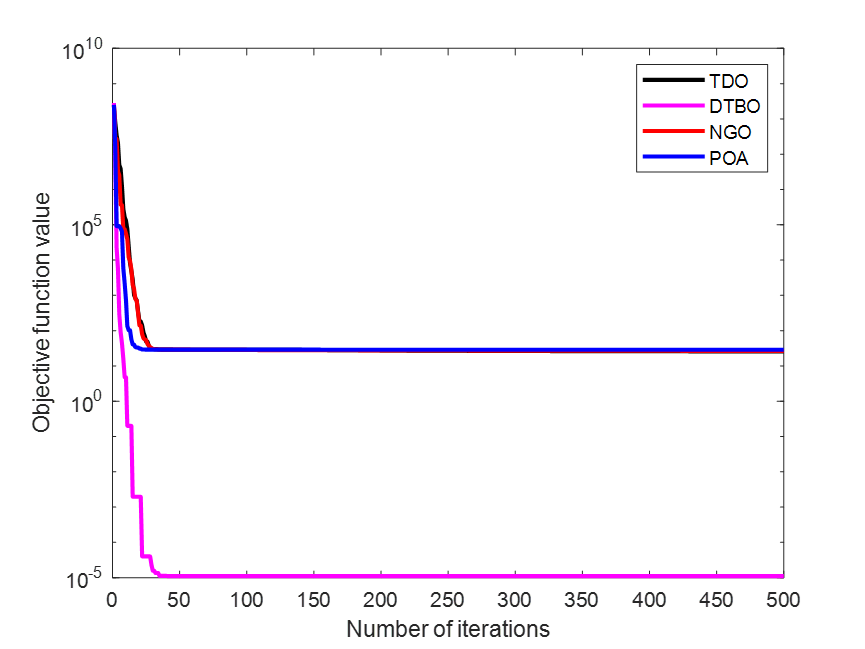
F5
??????
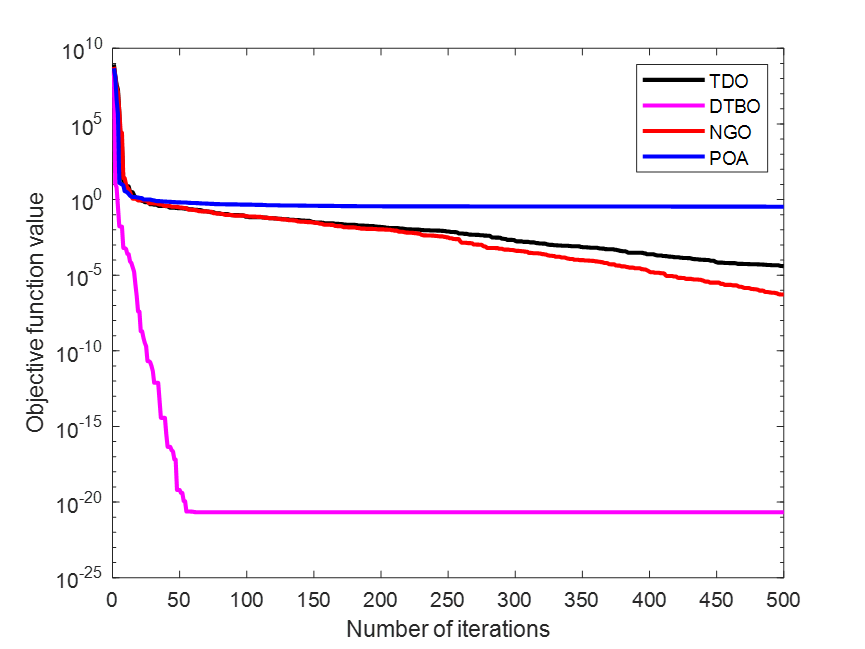
F12
??????
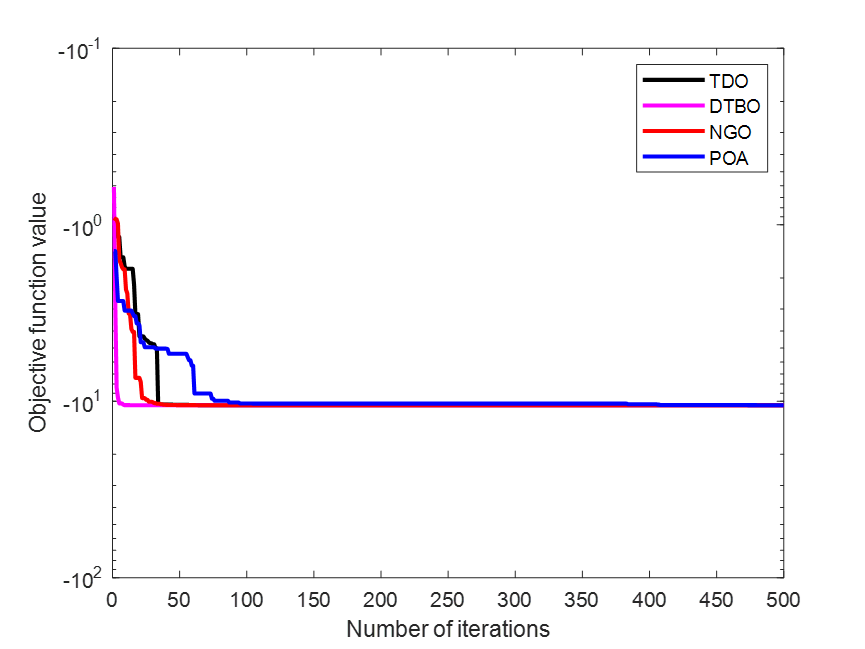
F23
??????
结果分析选择测试函数是F12
???????????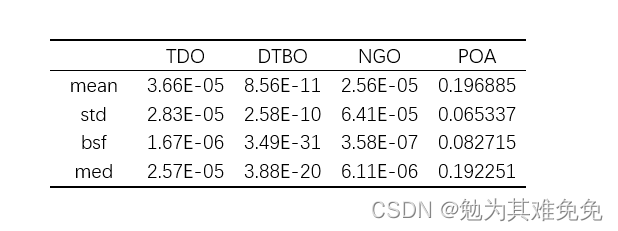
独立运行20次源码
%%
clc
clear
close all
%%
Fun_name='F12'; % number of test functions: 'F1' to 'F23'
SearchAgents=30; % number of Tasmanian Devil (population members)
Max_iterations=500; % maximum number of iteration
for i=1:20
[lowerbound,upperbound,dimension,fitness]=fun_info(Fun_name); % Object function information
[Best_score_TDO,Best_pos_TDO,TDO_curve]=TDO(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness);
[Best_score_DTBO,Best_pos_DTBO,DTBO_curve]=DTBO(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness);
[Best_score_NGO,Best_pos_NGO,NGO_curve]=NGO(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness);
[Best_score_POA,Best_pos_POA,POA_curve]=POA(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness);
result{i,:}=[Best_score_TDO,Best_score_DTBO,Best_score_NGO,Best_score_POA];
end
%% Result Analysis
format shortEng
fr=cell2mat(result);
fmean=mean(fr);
fstd=std(fr);
fbsf=min(fr);
fmedian=median(fr);
final=[fmean;fstd;fbsf;fmedian];
单独测试一个函数的源码
%%
clc
clear
close all
%%
Fun_name='F1'; % number of test functions: 'F1' to 'F23'
SearchAgents=30; % number of Tasmanian Devil (population members)
Max_iterations=500; % maximum number of iteration
[lowerbound,upperbound,dimension,fitness]=fun_info(Fun_name); % Object function information
for i=1:20
[Best_score_TDO,Best_pos_TDO,TDO_curve]=TDO(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness);
result(i)=Best_score_TDO;
end
display(['The mean obtained by TDO is : ', num2str( mean(result))]);%平均值
display(['The std obtained by TDO is : ', num2str( std(result))]); %标准差
display(['The var obtained by TDO is : ', num2str( var(result))]); %方差
学习交流,无偿分享已有源码
