【C++】高斯金字塔和拉普拉斯金字塔原理和实现
图像中各个像素与其相邻像素之间的有很强的相关性,包含的信息也十分丰富,目标的尺寸有大有小,对比度有强有弱,此时就需要一个“显微镜”或者“望远镜”-----多尺度图像技术。它可以在不同分辨率下观察目标的特征进而进行处理。
多尺度图像技术也叫做多分辨率技术(MRA),指对图像采用多尺度的表达,并且在不同尺度下分别进行处理。这样做的理由是很多情况下在一种尺度中不容易看清的或者获取的特性在另外的某种尺度下就很容易发现或者是提取。所以多尺度技术在提取图像特征时更加的常用。要在多尺度情况下对图像进行处理首先要在多尺度情况下对图像进行表达,并且找到各尺度之间的相互联系。而金字塔结构就是一种图像的多尺度表达形式。为了获得多尺度表达所采用的多尺度变换技术基本上可以分为三大类,尺度空间技术,时间尺度技术,时间频率技术。
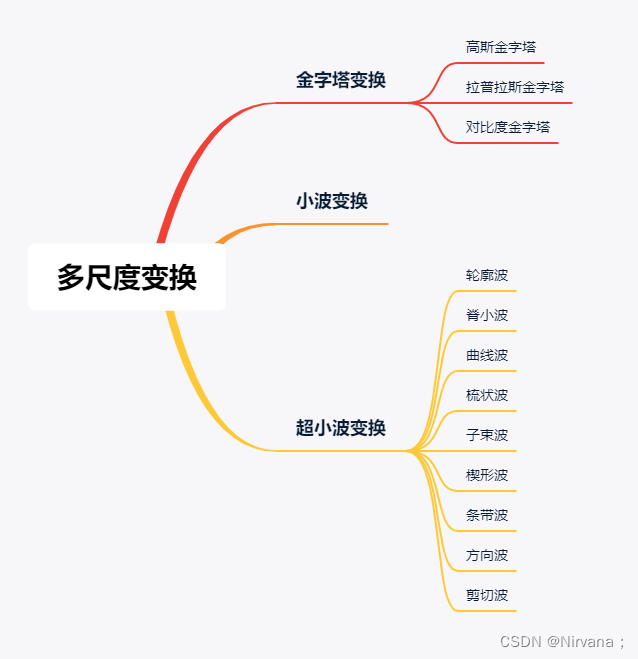
1. 图像金字塔
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。把具有最高级别分辨率的图像放在底部,以金字塔形状排列,往上是一系列像素(尺寸)逐渐降低的图像,一直到金字塔的顶部只包含一个像素点的图像,这就构成了传统意义上的图像金字塔。
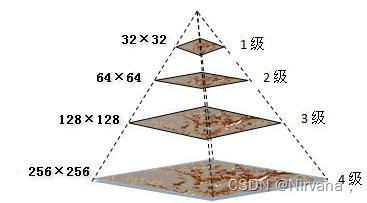
通过上采样和下采样实现图像金字塔,即对源图像的尺寸进行放大或者缩小变换。在opencv里面可以用resize函数,将源图像精准地转化为指定尺寸的目标图像。要缩小图像,一般推荐使用CV_INETR_AREA(区域插值)来插值;若要放大图像,推荐使用CV_INTER_LINEAR(线性插值)。这个函数可以用来做简单的图像尺度变换。
void resize(src,dst,size,int interpolation)
//src:源图像;dst:目标图像,
//size目标图像大小,可以是指定的尺寸或者放大缩小的比例
//指定插值方式,一般有四种插值方式可供选择,默认为线性插值法
图像金字塔效果如下:



2. 高斯金字塔
高斯金字塔(Gaussian pyramid): 通过高斯滤波和下采样获得一系列图像。相比于上面简单的下采样图像金字塔,高斯金字塔每一层都需要进行一次高斯滤波。通过使用不同的δ来调节高斯滤波器的频带宽度,得到经过不同高斯滤波器相同尺寸的同一组高斯金字塔。
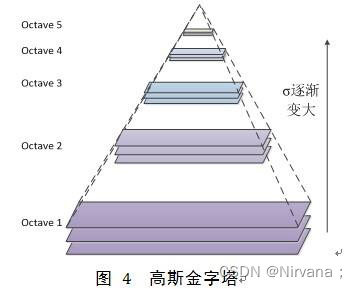
当图像向金字塔的上层移动时,尺寸和分辨率就降低。OpenCV中,从金字塔中上一级图像生成下一级图像的可以用PryDown。而通过PryUp将现有的图像在每个维度都放大两倍。
上采样:pyrUp()函数
void pyrUp(InputArray src, OutputArray dst, const Size& dstsize=Size());
上采样效果图如下:



下采样:pyrDown()函数
void pyrDown(InputArray src, OutputArray dst, const Size& dstsize=Size());
高斯金字塔效果图如下:



3. 拉普拉斯金字塔
拉普拉斯金字塔(Laplacian pyramid): 用来从金字塔低层图像重建上层未采样图像,在数字图像处理中也即是预测残差,可以对图像进行最大程度的还原,配合高斯金字塔一起使用。我们可以将拉普拉斯金字塔理解为高斯金字塔的逆过程形式。
拉普拉斯金字塔的计算过程是通过源图像减去先缩小后再放大的图像,可以直接用OpenCV进行拉普拉斯运算:
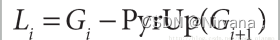
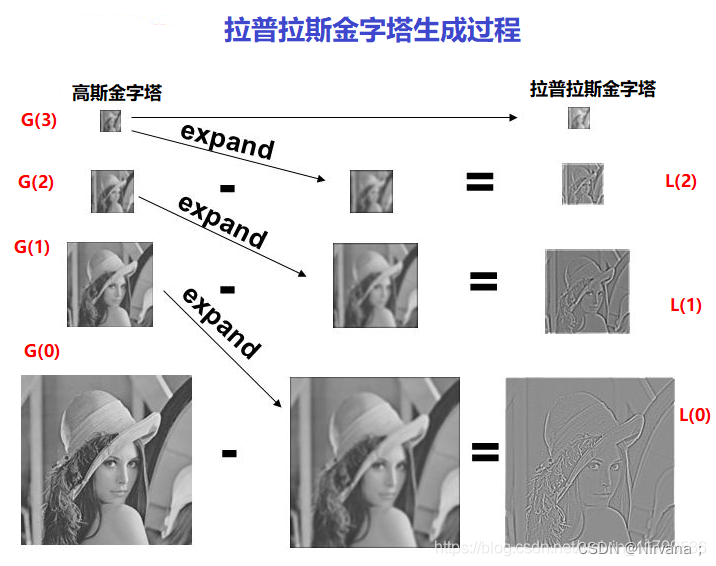
拉普拉斯效果图如下:



将拉普拉斯金字塔逐层上采样累加重构后的效果图如下:

C++和opencv代码实现:
#include "iostream"
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
void Gaussian_Pyramid(Mat &image, vector<Mat> &pyramid_images, int level);
void Laplaian_Pyramid(vector<Mat> &pyramid_images, Mat &image);
void reconstuction(int level);
int main(int argc, char** argv)
{
Mat src = imread("Curry.jpg");
/*copyMakeBorder(src, src, 0, 3, 0, 3, BORDER_REPLICATE);*/
imshow("01", src);
/*resize(src, src, Size(src.cols *4, src.rows *4));*/
/*cvtColor(src, src, COLOR_BGR2GRAY);*/
vector<Mat> p_images;
const int layer = 3; //金字塔层数
Gaussian_Pyramid(src, p_images, layer - 1);
Laplaian_Pyramid(p_images, src);
reconstuction(layer - 1);//从拉普拉斯金字塔恢复原图
waitKey();
return 0;
}
void Gaussian_Pyramid(Mat &image, vector<Mat> &pyramid_images, int level) {
Mat temp = image.clone();
Mat dst;
char buf[64];
for (int i = 0; i < level; i++) {
pyrDown(temp, dst);
imshow(format("pyramid_up_%d", i), dst);
sprintf_s(buf, "./result/gaussian_%d.jpg", i);
imwrite(buf, dst);
temp = dst.clone();
pyramid_images.push_back(temp);
}
}
void Laplaian_Pyramid(vector<Mat> &pyramid_images, Mat &image) {
int num = pyramid_images.size() - 1;
imwrite("./result/laplacian_0.jpg", pyramid_images[num]);
imshow("laplacian_0.jpg", pyramid_images[num]);
for (int t = num; t > -1; t--) {
Mat dst;
char buf[64];
if (t - 1 < 0) {
pyrUp(pyramid_images[t], dst, image.size());
subtract(image, dst, dst);
// dst = dst + Scalar(127, 127, 127);
sprintf_s(buf, "./result/laplacian_%d.jpg", num - t + 1);
imshow(buf, dst);
imwrite(buf, dst);
}
else {
pyrUp(pyramid_images[t], dst, pyramid_images[t - 1].size());
subtract(pyramid_images[t - 1], dst, dst);
// dst = dst + Scalar(127, 127, 127);
sprintf_s(buf, "./result/laplacian_%d.jpg", num - t + 1);
imshow(buf, dst);
imwrite(buf, dst);
}
}
}
void reconstuction(int level) {
char buf[64];
Mat dst = imread("./result/laplacian_0.jpg");
Mat dst2 = imread("./result/laplacian_1.jpg");
Mat dst3 = imread("./result/laplacian_2.jpg");
pyrUp(dst, dst);
Mat dst4 = dst + dst2;
pyrUp(dst4, dst4);
Mat dst5 = dst4 + dst3;
imshow("dst", dst5);
}
