一、粒子群算法优化极限学习机ELM简介
PSO-ELM优化算法预测模型
ELM模型在训练之前可以随机产生ω和b, 只需要确定隐含层神经元个数及隐含层神经元激活函数, 即可实现ELM预测模型的构建。在ELM模型的构建中, 只需确定初始ω和b, 而无需复杂的参数设置, 具有学习速度快、泛化性能好等优点。然而在发动机参数预测过程中, 不同的参数设置, 对预测模型的准确度起着一定程度的影响。此时, 如果通过简单的随机选取初始化参数方法来构建极限学习机模型, 在一定程度上存在着模型构建中隐含层节点冗余等缺点, 这在一定程度上阻碍了ELM模型的精确性。因此, 在构建EGTM数据预测模型的过程中, 可通过PSO算法寻优确定模型的最佳参数, 以保证ELM模型的准确性。
PSO优化算法于1995年由美国学者Eberhart和Kennedy提出。在优化过程中, 通过跟踪个体最优粒子pmbest与群体最优粒子gmbest, 从而更新粒子的速度与位置:

式中:d表示粒子搜索的空间维数, i为搜索过程中种群规模大小, m为当前种群代数。r∈(0,1), 表示随机数, c∈(0,2), 表示学习因子, 取值由经验设定。ω为惯性权重系数, 用x与v分别表示粒子的当前位置与当前速度, pmbest表示当前个体最优粒子位置, gmbest表示当前群体最优粒子位置。
利用PSO算法的收敛性强、鲁棒性好等优点, 可以在较短的运行时间内, 在保证精确度的情况下有效地寻找全局最优解。PSO-ELM算法的流程如图1所示。
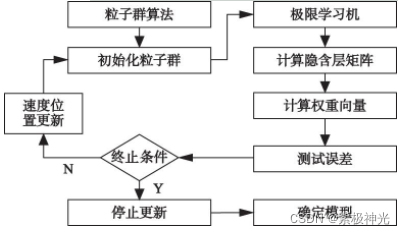
图1 PSO-ELM算法流程图
如图1所示, 在构建ELM预测模型的过程中, 利用PSO算法的参数优化能力, 通过建立适应值函数计算适应值, 以验证PSO算法中粒子的优劣。通过不断更新粒子, 以确保粒子不断趋向于全局最优。在预测过程中, 以预测结果与真实值之间的误差作为适应值函数, 通过寻找使得适应值函数最小的全局最优解, 从而确定更加精确的ELM预测模型, 为构建合理的ELM预测模型提供了理论基础。
二、部分源代码
clc
clear all
三、运行结果


四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]周品.MATLAB 神经网络设计与应用[M].清华大学出版社,2013.
[4]陈明.MATLAB神经网络原理与实例精解[M].清华大学出版社,2013.
[5]方清城.MATLAB R2016a神经网络设计与应用28个案例分析[M].清华大学出版社,2018.
[6]戴邵武,陈强强,刘志豪,戴洪德.基于粒子群极限学习机的排气温度裕度预测[J].仪表技术. 2019,(06)
