[人工智能] SFR算法与OpenCV联合开发----评价图像清晰度(解析力)

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> SFR算法与OpenCV联合开发----评价图像清晰度(解析力) -> 正文阅读

[人工智能]SFR算法与OpenCV联合开发----评价图像清晰度(解析力)

免责声明：仅供研究讨论，未经确认，相关内容严禁商用，若有错误，欢迎指正。
本文会给出如何开发的方法以及源代码。
关于MTF与SFR的介绍：

MTF

成像画面的清晰度，表示分辨细节的能力
MTF（Modulation Transfer Function）曲线的定义：
MTF曲线图显示的是镜头对对比度的还原情况，纵轴表示优劣，横轴表示空间频率（单位：Lp/mm-线对/mm））。Ps：也有横轴表示与成像中心的距离，不主要讲述。
空间频率：在1个mm中能分辨以下的多少线对，一黑一白为一个线对。

MTF----百度百科，看懂这一篇就够了

以下为百科文章的关于MTF 曲线的论述，后面紧跟MTF曲线的个人注解：
MTF曲线图的意义
镜头的成像品质是影友们最为关心，也是争论最多的话题，虽然各种针对镜头成像素质的测试方法层出不穷，但由于测试条件千差万别，因此这些方法都不能非常准确地反应镜头的真实品质。与媒体拍摄分辨率标板的测试方法相比，MTF 成像曲线图是由镜头的生产厂家在极为客观严谨的测试环境下测得并对外公布的，是镜头成像品质最权威、最客观的技术参考依据。下面就来介绍MTF 曲线的技术原理和解读方法.
测量反差与分辨率
众所周知，对数码照片成像素质影响最大的是镜头的分辨率和反差。分辨率的单位是线对/ 毫米（lp/mm），相邻的黑白两条线可以称为一个线对，每毫米能够分辨出的线对数就是分辨率。如何测试镜头的分辨率和反差呢？厂商利用拍摄正弦光栅（测试标板中的黑白相间的栅格）的方法进行测试，亮度按正弦变化的周期图形叫做“正弦光栅”。而正弦光栅的疏密程度被称为“空间频率”（Spatial Frequency），空间频率的单位用lp/mm 表示。lp/mm 标识单位长度( 每毫米) 的亮度按照正弦变化的图形的周期数。
反差与正弦光栅分辨率
我们再回过头来看反差。
反差 =（照度的最大值-照度的最小值） /（照度的最大值 + 照度的最小值）。
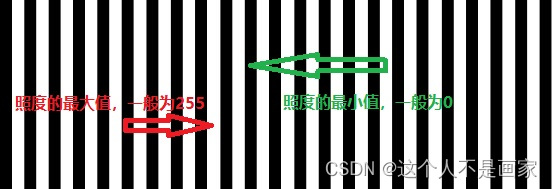
在这里插入图片描述

所以，反差的数值总是小于等于1 的。这里我们引入调制度M 的概念：
M=（Imax － Imin）/（Imax + Imin）
调制度M 总是介于0 和1 之间，调制度越大，反差越大。在对镜头的反差和分辨率进行测试时，我们将正弦光栅置于镜头前方，测量镜头成像处的调制度。这时由于镜头像差的影响，会出现以下情况。当空间频率很低时，测量出的调制度M 几乎等于正弦光栅的调制度；当所拍摄的正弦光栅空间频率提高时，镜头成像的调制度逐渐下降。镜头成像的调制度随空间频率变化的函数称为调制度传递函数MTF（Modulation Transfer Function）。对于原来调制度为M 的正弦光栅，如果经过镜头到达像平面的像的调制度为M ’ ，则MTF函数值为：
MTF 值= M ’ / M
在这里我们假设M是固定的，为1
如果原图经过镜头与sensor采集后，出现的黑白线对模糊，那么照度最小值就会大于0，同时照度最大值就会小于255了。也就是会出现灰色模糊。
所以计算得到的MTF 值= M ’ / M一般情况下总会小于等于1
这就是为什么MTF值在空间频率比较低的时候总是接近于1，在空间频率增高的时候会变小的原因
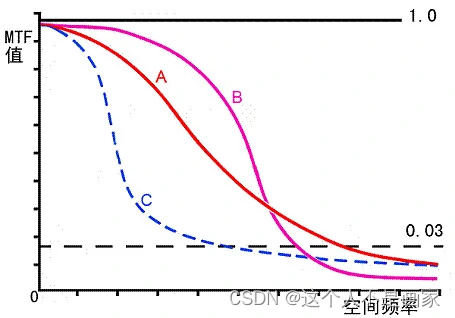
在这里插入图片描述

由此可见，MTF 值必定大于0，小于1。MTF 值越接近1，说明镜头的性能越优异。
MTF 值不但可以反映镜头的反差，也可以反映镜头的分辨率。由于MTF 值是厂商在严谨的测试环境下测得的，排除了成像介质（胶片或感光元件）的影响，因此较为客观。当空间频率很低时，MTF 趋于1，这时的MTF 值可以反映镜头的反差。当空间频率提高，也就是正弦光栅的密度提高时，MTF 值逐渐下降，这时的MTF 曲线可以反映镜头的分辨率。由于人眼的分辨能力有限，我们一般取MTF 值为0.03时的空间频率作为镜头的目视分辨率极限。空间频率高于这个值时，镜头成像素质的变化人眼难以察觉，也就不存在测量的意义了。

SFR

图像解析力算法—SFR（Spatial Frequency Response）概念理解

图像解析力算法—SFR（Spatial Frequency Response）原理分析(一)

图像解析力算法—SFR（Spatial Frequency Response）原理分析(二)

关于SFR源码解析：
图像解析力算法—SFR（Spatial Frequency Response）源码分析(一）
图像解析力算法—SFR（Spatial Frequency Response）源码分析(二)–完
 汉明窗1
汉明窗2
SFR算法详解（一）——基础理论
 SFR算法详解（二）——斜棱法

以下为个人注解版SFR算法与OPENCV 的联合开发源代码：

int main() {
	cout<<"blockTest_ori.jpg"<<endl;
	cout<<CalSFR(imread("blockTest_ori.jpg",0))<<endl;
	cout<<"**********************************"<<endl;
	cout<<"blockTest300.jpg.jpg"<<endl;
	cout<<CalSFR(imread("blockTest300.jpg",0))<<endl;
	cout<<"**********************************"<<endl;
	cout<<"blockTest200.jpg.jpg"<<endl;
	cout<<CalSFR(imread("blockTest200.jpg",0))<<endl;
	cout<<"**********************************"<<endl;
	cout<<"blockTest100.jpg"<<endl;
	cout<<CalSFR(imread("blockTest100.jpg",0))<<endl;
	cout<<"**********************************"<<endl;
	cout<<"blockTest50.jpg"<<endl;
	cout<<CalSFR(imread("blockTest50.jpg",0))<<endl;
	cout<<"**********************************"<<endl;
	cout<<"blockTest25.jpg"<<endl;
	cout<<CalSFR(imread("blockTest25.jpg",0))<<endl;
	cout<<"**********************************"<<endl;
	system("pause");
	return 0;
}