第五章主要讲的是编程语言的介绍,因为我们现在用python的比较多,所以就没有再看那一章。但是5.6值得看一下
5.6 矢量
现在的变成语言包含了各种各样的矩阵库,所以通常进行矩阵计算的时候我们直接用命令即可,如果使用了合适的向量化方法,代码会简单很多。
下面进行一些例子的讲解。
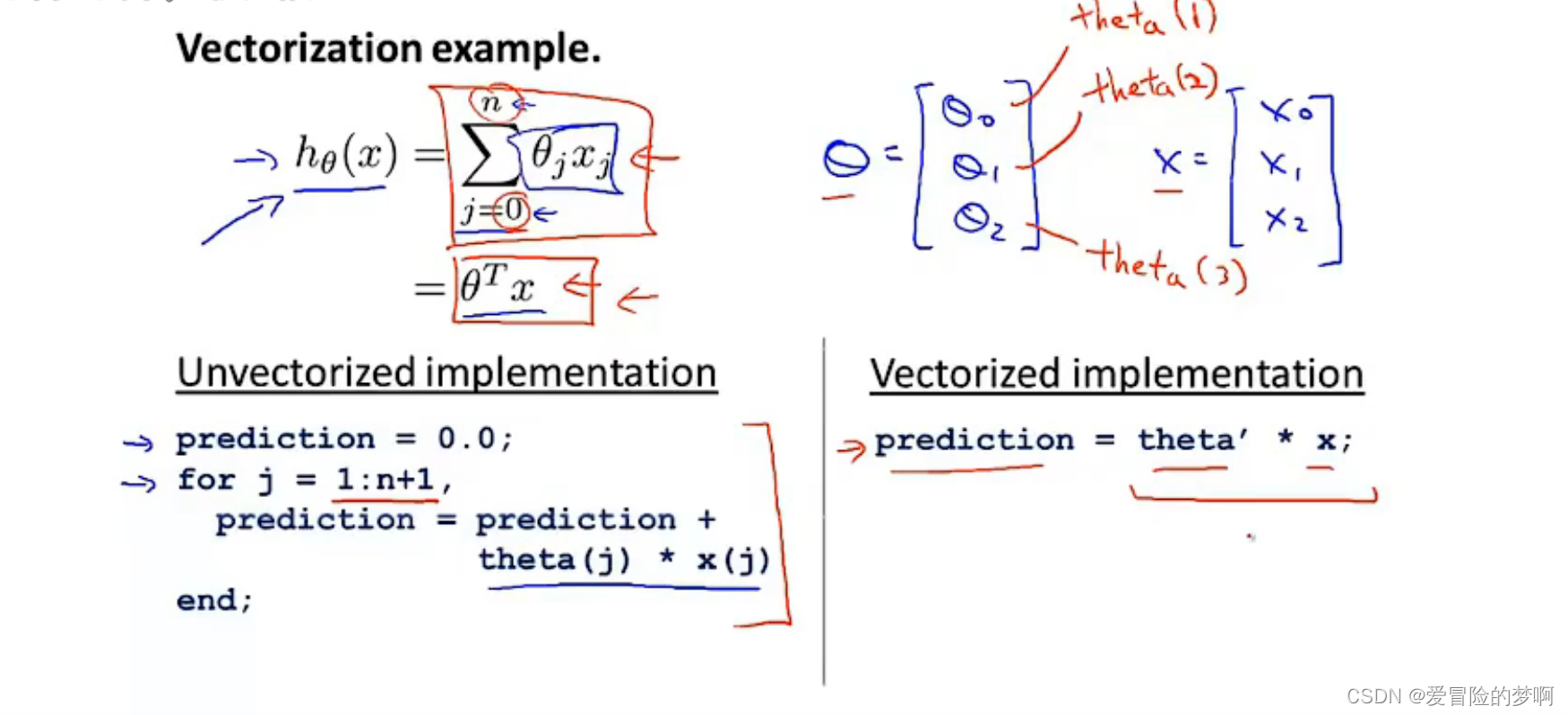
这是线性回归的假设函数,他是从0到j的一个求和,我们也可以把他看作是矩阵的相乘,θ的转置×x,可以写成计算两个向量的内积。
前面的如果要是用代码实现的话,就要用到for循环,因为从0到j,后面的用代码的话直接用矩阵相乘即可。
这是梯度下降的公式,我们用向量化来进行表示。
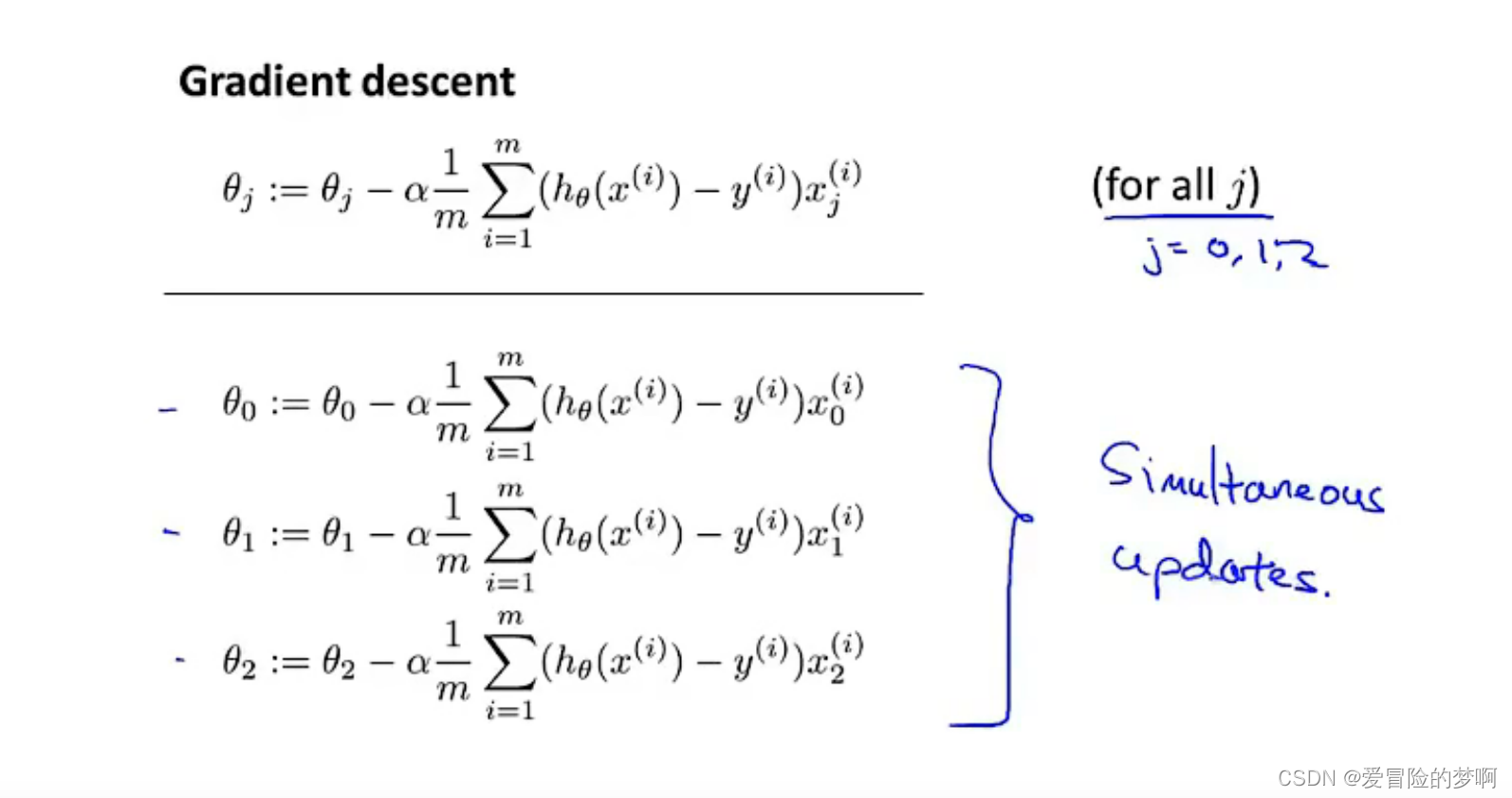
这里把看作θ是n+1维的向量,α是个实数,δ也是n+1维的向量,所以梯度更新实际上是一个向量的减法运算。其中粉红色的预测的减去实际的值是个实数,Xi是个向量,这样里面的加和就可以像u=3v+5w的形式去表示,也就是向量的加法。

最后,如果你在实施线性回归的时候,使用两个以上的特征量,有时我们在线性回归中使用几十甚至上百个特征,当使用向量化 实现线性回归时,相比于for循环速度更快。
6.1 分类
从这节开始,我们讨论预测的变量y是一个离散的值的时候下的分类问题。

这里的分类问题不像是我们之前讨论的预测房价啊,从0到10000等等,这里的分类是要么是0,要么是1.
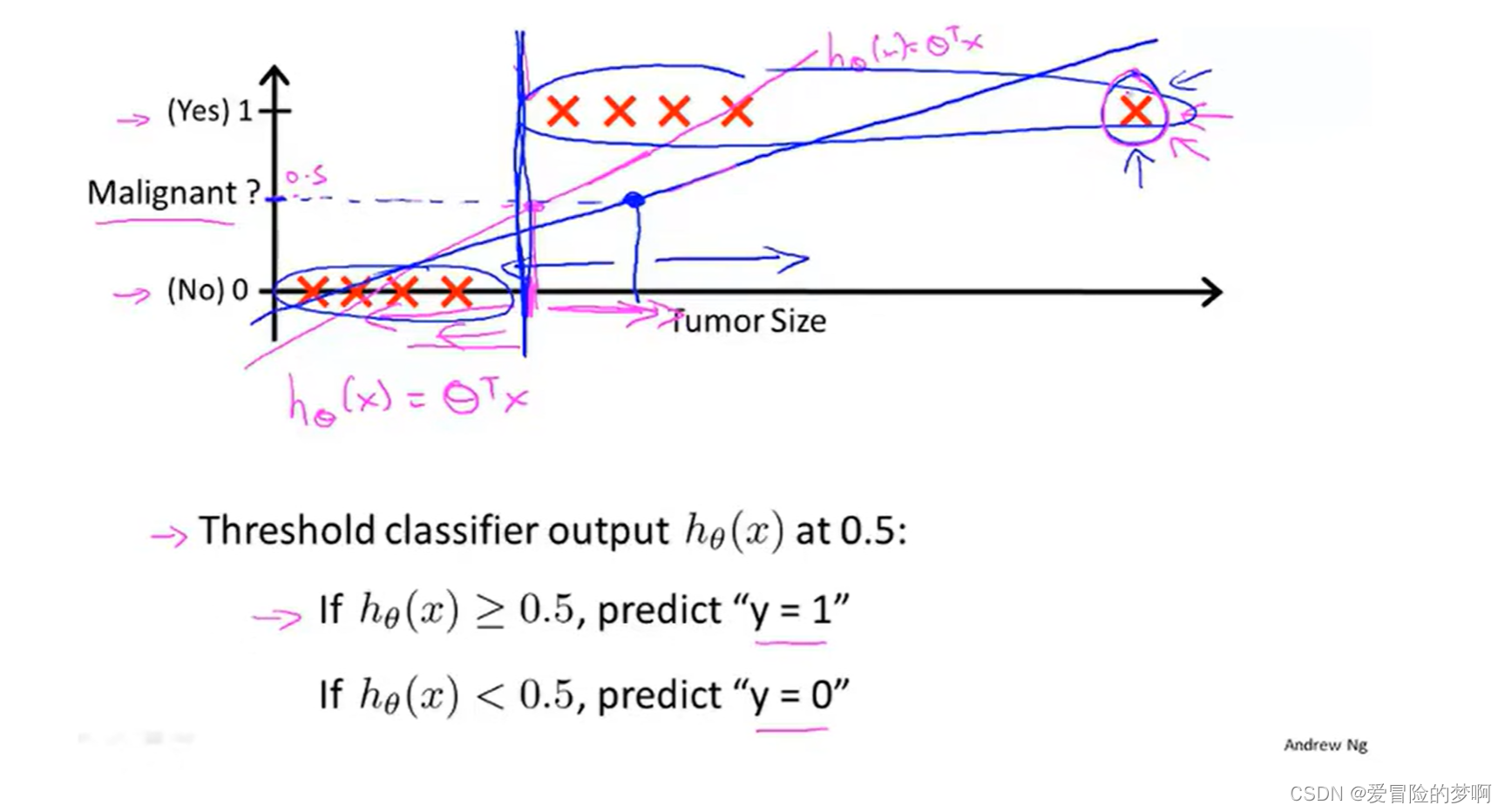
如图所示,我们用线性回归进行数据的拟合的时候,可能一开始还比较实用,但是当出现另一个点的时候,这时候我们要调整线性回归的曲线,来调整曲线拟合,这样正确率不高并且不方便。所以讲线性回归应用到分类问题是不合适的。
对于假设函数输出可能是大于1或者小于0的,但是我们目标的标签是0或者1,所以我们就引入了逻辑回归(Logistic Regression)他利用sigmoid函数可以讲输出压缩在0-1之间。

6.2 假设陈述
逻辑回归就是用了下图所示的sigmoid函数,将输出压缩到0-1之间
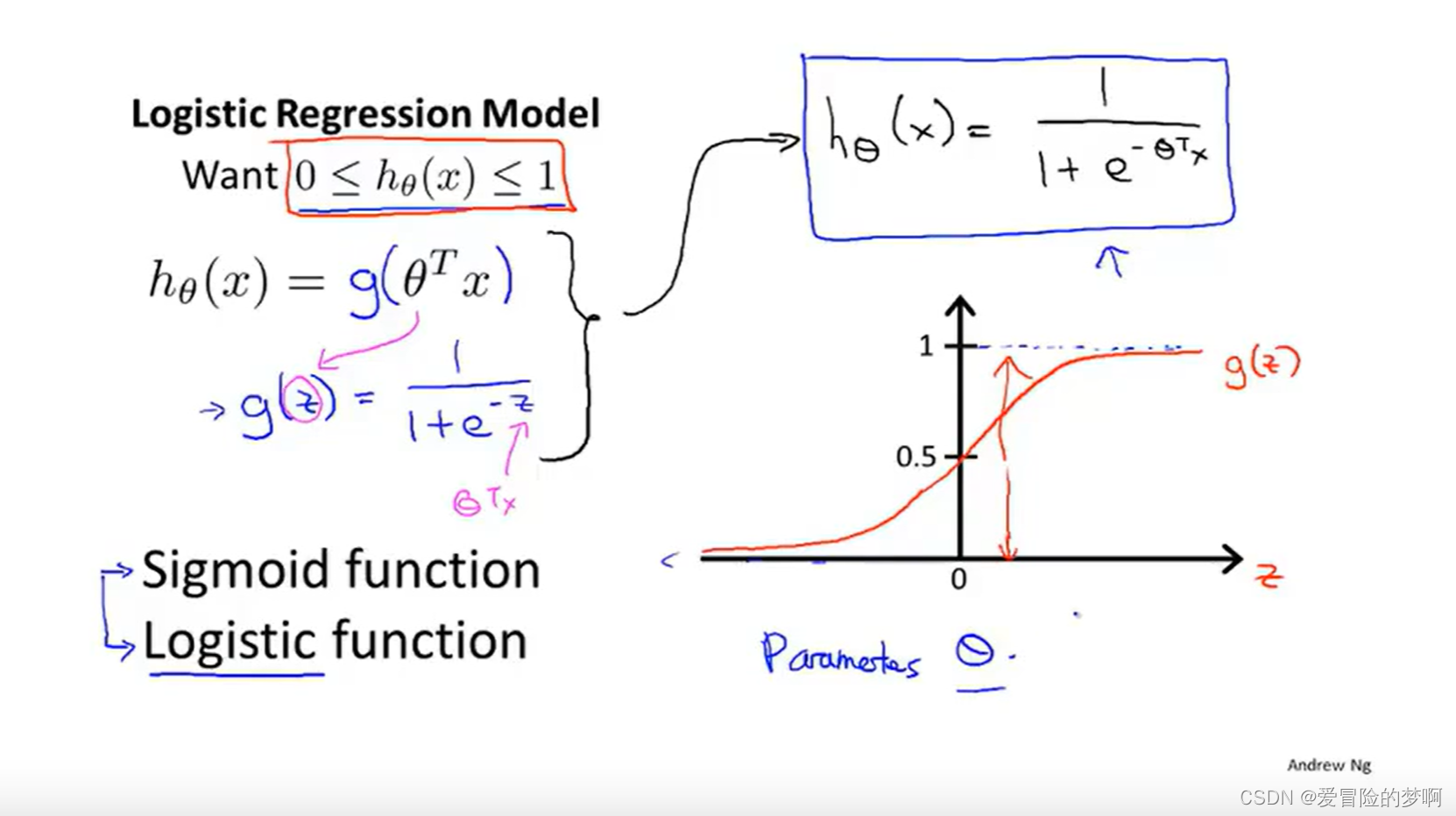
下面是对假设输出的解释,当假设输出输出一个数字的时候,我们会将这个数字当作对一个输入x,y等于1的概率估计。
我觉得可以理解为h(x)是当输入为x的时候,输出y等于1的概率有多大
下面是个例子来解释。x特征和之前一样,一个是1,一个是肿瘤的大小,将他的特征喂给我的假设中,并且假设我的假设输出是0.7,这个假设告诉我们对于一个特征为x的患者,y=1的概率是0.7,也就是百分之70的概率这个肿瘤是恶性的。我们用数学的式子来表示,下面这个图中的式子表述在给定X的条件下y=1的概率,即病人的特征为x的情况下,也就是代表着肿瘤的大小,这个概率的参数为θ(条件概率)

