1、状态估计问题
1、批量状态估计与最大后验估计
首先回顾以下经典SLAM模型：
从前面的文章可以知道，xk就是相机的位姿，uk为传感器输入，zk,j为我们得到的像素位置，观测方程就是我们说过的针孔相机模型。
在运动和观测方程中，我们通常假设两个噪声项wk，vk,j满足零均值的高斯分布，表示如下：
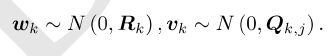
在这些噪声的影响下，我们想通过已知的Zk,j和传感器数据u来推断出位姿x(定位）和地图y(建图)以及他们的概率分布，这样的问题我们称为状态估计问题。
处理这类问题有批量式处理和增量式(滤波器）处理两种处理办法，本章我们介绍批量式处理方法。
批量式处理是把数据攒在一起来处理，比如我们收集0——k时刻的所有观测和输入数据并放在一起，在这样的0——k时刻的数据下，如何估计x和y？
接下来我们考虑0——N时刻，并且有M个路标点，定义所有时刻机器人的位姿和路标点坐标为：
同样，用u来代表传感器输入，z代表观测数据，对机器人的状态估计，从概率学角度上来说就是已知输入数据u和观测数据z的条件下，求状态x，y的概率分布。
?当我们只有一张张照片的时候，就变成只知道z的情况下求x，y的条件概率分布。
?为了估计x，y条件分布，引用贝叶斯公式：
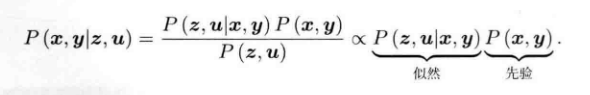
?贝叶斯法则等式左侧是后验概率，右侧为似然和先验，贝叶斯法则等式右侧的分母部分和x，y无关所以可以忽略，这样我们想要求得后验概率最大，也可以转换为最大化似然和先验部分的乘积。
?如果说我们都不知道机器人的位姿和路标位置，那么只需要最大化似然即可。也就是说，求解最大后验概率可以转化为一个求解最大似然估计。
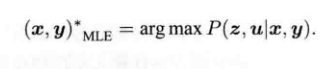
?直观的解释SLAM中的最大似然估计就是，在我们已经知道图片z的情况下，x和y应该在什么状态下，最可能产生图片z。
2、最小二乘引出
上面我们说过，视觉slam问题是要解决在已经知道图片z的情况下来估计x(定位）y（建图）。这样就转化为求一个后验概率的问题：
但是直接求后验概率很不方便，所以通过贝叶斯公式我们发现可以求解一个最大似然估计。那么如何求解最大似然估计？
我们知道在高斯分布下，最大似然估计可以很好的解决，假设噪声符合高斯分布：
?那么在噪声影响下的观测数据也会服从高斯分布：
?我们知道，任意高维高斯分布
他的概率密度函数为：
?由于是指数的形式，我们取负对数的形式更方便运算：
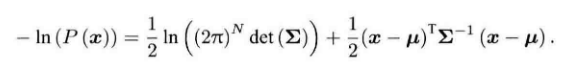
?由于对数函数是单调递减的，所以对原函数求最大化相当于对负对数求最小化，也即是最小化上式的x，由于等式右边第一项和x无关所以可以忽略，所以我们只需要最小化等式右边的二次型项就会完成最大似然估计。
将slam的观测模型带入上面的通式中：
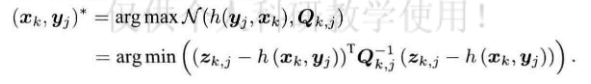
zk,j是得到的数据，h函数中如果没有噪声得到的数据，所以上式等价于最小化噪声项的一个二次型。这个二次型可以叫做马氏距离。
上面我们讨论的是某一次的观测信息，并且推导出了最小二乘法，接下来我们讨论批量时刻的数据。我们假设各个时刻的输入和观测是相互独立的,这意味着各输入是相互独立的，各观测也是相互独立的，输入和观测也是相互独立的。那么我们可以把批量的数据的似然写为：
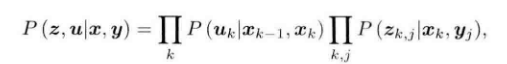
?上面我们推导出最大似然估计实际是最小化噪声项的一个二次型。噪声项就是输入和观测数据与模型之间的误差，我们记为：
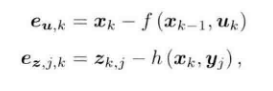
?我们将误差带入二次型中，最小化这个二次型便是等价于最大似然估计：
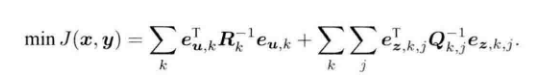
?以上便是最小二乘问题，对最小二乘问题的求解等价于求解最大似然估计。上面的式子直观的来看可以解释为，当我们把估计的轨迹和地图带入SLAM运动，观测方程中，由于噪声的存在，他不会完美的成立。我们可能无法避免，但是可以微调来减小误差，换句话说就是可以减小噪声，这个逐渐微调减小误差的过程便是非线性优化的问题。
3、非线性最小二乘
上面引出了最小二乘，那么接下来就需要对其进行优化，常用的优化方式便是求导，寻找最小值。
我们先引入一个十分简单的最小二乘问题：
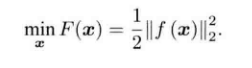
?接下来考虑优化问题，如果上式的f是一个很简单函数，那么我们可以直接令目标导数为0，求解x便可以得出最优值。
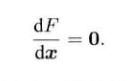
?但是方程是否易于求解取决于f导数的形式，如果是很简单线性函数，那么问题会很简单，但有些问题很复杂，f是一个非线性函数，f的导函数不易于我们求解，我们就不能用上述方法。
对于不方便直接求解的最小二乘问题，我们可以采用迭代的方式来求解，选择一个初始值，给一个步长，不断更新当前的优化变量，具体步骤为：
?上述方法是一个不断寻找下降增量Δx的问题，当Δx足够小，就可以认为收敛，目标函数达到了极小值。那么如何选择Δx就是接下来要说的内容。
1、一阶和二阶梯度法
假设我们考虑第k次迭代，在xk处想要寻找增量Δx，我们将目标函数在xk附近泰勒展开：
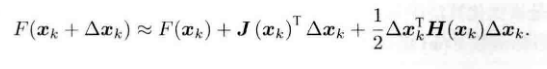
?J(xk)是F(x)关于x的一阶导数，H则是二阶导数，也叫做海塞矩阵。
如果保留一阶梯度，那么我们取增量为和梯度方向相反的方向，可以保证函数下降最快，同时，我们还需要指定一个步长来控制一次要下降多少。这样的方法称为最速下降法，直观意义就是沿着梯度的相反方向，目标函数必会下降。
如果保留二阶梯度，此时增量方程为：
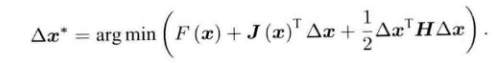
?求等式右侧关于Δx的导数并令其为0可以得到：
?这样的方法称为二阶梯度法，也叫牛顿法。
一阶和二阶看起来都很直观，但是一阶梯度太过于注重眼前，容易增加迭代次数，牛顿法需要计算H矩阵，实际上H矩阵的计算是非常繁琐的。对于最小二乘问题，还有高斯牛顿法和列文伯格-马尔夸特法。
2、高斯牛顿法
高斯牛顿法是将f(x)进行一阶泰勒展开，而不是上述一阶梯度法的F(x)。
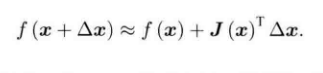
?J(x)为f(x)关于x的导数，我们的目的是寻找Δx，使得
最小，那么我们转成最小二乘问题：
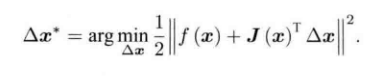
?将上述的平方项展开：
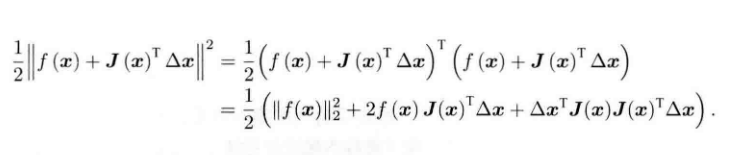
?求上式对Δx的导数，并令其为0：
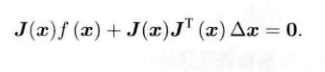
?整理后得到：
?我们称上述方程为高斯牛顿方程，将等式左边系数用H表示，右边用g表示：
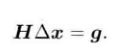
?高斯牛顿法将
近似代替了牛顿法中的H矩阵，减少了计算量，所以高斯牛顿法的关键在于求解增量方程，步骤如下：
?但是高斯牛顿法也有不足，虽然他近似了牛顿法中的H矩阵，但是在一些情况下，这个近似是不成立的，近似的H矩阵只有半正定性，为了解决这个问题，我们引入了列文伯格-马尔夸特法。
3、列文伯格-马尔夸特法
上面的高斯牛顿法说了H矩阵只是近似出来的，在一些情况下无法近似H矩阵。马尔夸特法给出了信赖区域，指出了Δx在什么范围内是近似有效的，在什么范围内近似可能会出问题。
那么如何定义这个信赖区域的范围呢？一个好的办法是根据我们地近似模型跟实际函数的差异来确定，差异小，说明近似效果好，我们可以扩大近似范围，如果差异大，那么我们就要缩小近似范围。
?分子是实际模型下降的值，分母是近似模型下降的值。如果ρ接近1，说明近似是好的，如果ρ太小，说明实际下降的远小于近似的，认为近似差，需要缩小范围，反之ρ如果大，说明实际下降的比预计的大，可以扩大近似范围。所以算法框架为：
?上述式子和高斯牛顿法不同的地方在于，需要解决一个拉格朗日函数的问题：
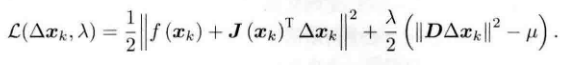
?令该函数关于Δx的导数为0可以得出;
?相比高斯牛顿法，多出来一个
令D =I为一个单位矩阵就变为：
?
?
?
?
?
?
?
?
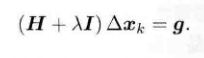
