1. Data Prepation

1.1 加载数据集

# load data in folder datasets
mnist = input_data.read_data_sets('datasets', one_hot=False)

train_data = mnist.train.images.astype(np.float32)
val_data = mnist.validation.images.astype(np.float32)
test_data = mnist.test.images.astype(np.float32)
train_labels = mnist.train.labels
val_labels = mnist.validation.labels
test_labels = mnist.test.labels

train_data_shape:55000,784

val_data_shape:5000,784

test_data_shape:1000,784

train_label_shape:55000

解释：训练集共计55000张图片，每张图片都是28*28的，每个特征的数值是01型。所有的数组类型都为ndarray型数组

1.2 构造图

1.2.1 构造大小为m的网格

def grid(m, dtype=np.float32):
    """Return coordinates of grid points"""
    M = m**2  # 784=28*28
    x = np.linspace(0,1,m, dtype=dtype)  # 生成大小为784的0-1之间的等间距的小数数组x
    y = np.linspace(0,1,m, dtype=dtype)  # 生成大小为784的0-1之间的等间距的小数数组y
    xx, yy = np.meshgrid(x, y)  # shape(28,28)
    z = np.empty((M,2), dtype)  # shape(784,2)
    z[:,0] = xx.reshape(M)
    z[:,1] = yy.reshape(M)
    return z

np.linspace(start, stop, num, endpoint, retstep, dtype)

star和stop为起始和终止位置，均为标量
num为包括start和stop的间隔点总数，默认为50
endpoint为bool值，为False时将会去掉最后一个点计算间隔
restep为bool值，为True时会同时返回数据列表和间隔值
dtype默认为输入变量的类型，给定类型后将会把生成的数组类型转为目标类型
这是一个可以生成等间距数组的的一个函数，还是蛮常用的，最重要的就是前三个参数

X, Y = np.meshgrid(x, y) 代表的是将x中每一个数据和y中每一个数据组合生成很多点,然后将这些点的x坐标放入到X中,y坐标放入Y中,并且相应位置是对应的

np.empty() 函数语法如下：

empty(shape[, dtype, order])

依给定的shape, 和数据类型 dtype, 返回一个一维或者多维数组，数组的元素不为空，为随机产生的数据。

其中参数解释如下：

shape：整数或者整型元组定义的返回数组的形状。

dtype：数据类型，定义返回数组的类型，可选。如dtype = int

order: {‘C’, ‘F’}, 规定返回数组元素在内存的存储顺序。

1.2.2 计算成对距离

def distance_sklearn_metrics(z, k=4, metric='euclidean'):
    """Compute pairwise distances"""
    d = sklearn.metrics.pairwise.pairwise_distances(z, metric=metric, n_jobs=1)  # 计算z中两两行之间的距离，shape(784,784)
    # k-NN
    idx = np.argsort(d)[:,1:k+1]  # 将每一行分别排序后获取排序后的下标，获取每一行中与其距离最近的8行，shape(784,8)
    d.sort()  # 将每一行分别排序
    d = d[:,1:k+1]  # 获取每一行与其距离最近的8行的距离值
    return d, idx  # 返回每一行中与其距离最近的8行的下标与距离值

sklearn.metrics.pairwise_distances(X, Y=None, metric=’euclidean’, n_jobs=None, **kwds)

根据向量数组X和可选的Y计算距离矩阵。
此方法采用向量数组或距离矩阵，然后返回距离矩阵。如果输入是向量数组，则计算距离。如果输入是距离矩阵，则将其返回。
如果给出了Y（默认值为None），则返回的矩阵是数组之间从X和Y开始的成对距离。

argsort(x)函数是将x中的元素从小到大排列，提取其对应的index(索引)，然后返回

1.2.3 构造图的邻接稀疏权重矩阵

def adjacency(dist, idx):
    """Return adjacency matrix of a kNN graph"""
    M, k = dist.shape
    assert M, k == idx.shape
    assert dist.min() >= 0
    assert dist.max() <= 1

    # Pairwise distances
    sigma2 = np.mean(dist[:,-1])**2
    dist = np.exp(- dist**2 / sigma2)  # 将距离标准化

    # Weight matrix
    I = np.arange(0, M).repeat(k)  #shape(784*8=6272,)
    J = idx.reshape(M*k)  #shape(784*8=6272,)
    V = dist.reshape(M*k)  #shape(784*8=6272,)
    W = scipy.sparse.coo_matrix((V, (I, J)), shape=(M, M))  # 构造I*J的稀疏矩阵，对应非0的值为V

    # No self-connections
    W.setdiag(0)  # 对角线的值设置为0

    # Undirected graph
    bigger = W.T > W
    W = W - W.multiply(bigger) + W.T.multiply(bigger)

    assert W.nnz % 2 == 0  # 判断非零个数是否为偶数
    assert np.abs(W - W.T).mean() < 1e-10
    assert type(W) is scipy.sparse.csr.csr_matrix
    return W

1.2.4 构造网格图

def grid_graph(grid_side,number_edges,metric):
    """Generate graph of a grid"""
    z = grid(grid_side)
    dist, idx = distance_sklearn_metrics(z, k=number_edges, metric=metric)
    A = adjacency(dist, idx)   # shape(784, 784)的一个系数稀疏矩阵
    print("nb edges: ",A.nnz)  # 稀疏矩阵中有6396个零
    return A  # 返回邻接稀疏权重矩阵

1.3 计算粗话图

1.3.1 重边匹配HEM

def HEM(W, levels, rid=None):
    """
    Coarsen a graph multiple times using the Heavy Edge Matching (HEM).

    Input
    W: symmetric sparse weight (adjacency) matrix
    levels: the number of coarsened graphs

    Output
    graph[0]: original graph of size N_1
    graph[2]: coarser graph of size N_2 < N_1
    graph[levels]: coarsest graph of Size N_levels < ... < N_2 < N_1
    parents[i] is a vector of size N_i with entries ranging from 1 to N_{i+1}
        which indicate the parents in the coarser graph[i+1]
    nd_sz{i} is a vector of size N_i that contains the size of the supernode in the graph{i}

    Note
    if "graph" is a list of length k, then "parents" will be a list of length k-1
    """

    N, N = W.shape
    
    if rid is None:
        rid = np.random.permutation(range(N))
        
    ss = np.array(W.sum(axis=0)).squeeze()
    rid = np.argsort(ss)
        
        
    parents = []
    degree = W.sum(axis=0) - W.diagonal()
    graphs = []
    graphs.append(W)

    print('Heavy Edge Matching coarsening with Xavier version')

    for _ in range(levels):

        weights = degree            # graclus weights
        weights = np.array(weights).squeeze()

        # PAIR THE VERTICES AND CONSTRUCT THE ROOT VECTOR
        idx_row, idx_col, val = scipy.sparse.find(W)
        cc = idx_row
        rr = idx_col
        vv = val

        if not (list(cc)==list(np.sort(cc))):
            tmp=cc
            cc=rr
            rr=tmp

        cluster_id = HEM_one_level(cc,rr,vv,rid,weights)
        parents.append(cluster_id)

        # COMPUTE THE EDGES WEIGHTS FOR THE NEW GRAPH
        nrr = cluster_id[rr]
        ncc = cluster_id[cc]
        nvv = vv
        Nnew = cluster_id.max() + 1
        # CSR is more appropriate: row,val pairs appear multiple times
        W = scipy.sparse.csr_matrix((nvv,(nrr,ncc)), shape=(Nnew,Nnew))
        W.eliminate_zeros()
        
        # Add new graph to the list of all coarsened graphs
        graphs.append(W)
        N, N = W.shape

        # COMPUTE THE DEGREE (OMIT OR NOT SELF LOOPS)
        degree = W.sum(axis=0)

        # CHOOSE THE ORDER IN WHICH VERTICES WILL BE VISTED AT THE NEXT PASS
        ss = np.array(W.sum(axis=0)).squeeze()
        rid = np.argsort(ss)

    return graphs, parents

1.3.2 构造二叉树

def compute_perm(parents):
    """
    Return a list of indices to reorder the adjacency and data matrices so
    that the union of two neighbors from layer to layer forms a binary tree.
    """

    # Order of last layer is random (chosen by the clustering algorithm).
    indices = []
    if len(parents) > 0:
        M_last = max(parents[-1]) + 1
        indices.append(list(range(M_last)))

    for parent in parents[::-1]:

        # Fake nodes go after real ones.
        pool_singeltons = len(parent)

        indices_layer = []
        for i in indices[-1]:
            indices_node = list(np.where(parent == i)[0])
            assert 0 <= len(indices_node) <= 2

            # Add a node to go with a singelton.
            if len(indices_node) is 1:
                indices_node.append(pool_singeltons)
                pool_singeltons += 1

            # Add two nodes as children of a singelton in the parent.
            elif len(indices_node) is 0:
                indices_node.append(pool_singeltons+0)
                indices_node.append(pool_singeltons+1)
                pool_singeltons += 2

            indices_layer.extend(indices_node)
        indices.append(indices_layer)

    # Sanity checks.
    for i,indices_layer in enumerate(indices):
        M = M_last*2**i
        # Reduction by 2 at each layer (binary tree).
        assert len(indices[0] == M)
        # The new ordering does not omit an indice.
        assert sorted(indices_layer) == list(range(M))

    return indices[::-1]

assert (compute_perm([np.array([4,1,1,2,2,3,0,0,3]),np.array([2,1,0,1,0])])
        == [[3,4,0,9,1,2,5,8,6,7,10,11],[2,4,1,3,0,5],[0,1,2]])

1.3.3 构造聚类树

def perm_adjacency(A, indices):
    """
    Permute adjacency matrix, i.e. exchange node ids,
    so that binary unions form the clustering tree.
    """
    if indices is None:
        return A

    M, M = A.shape
    Mnew = len(indices)
    A = A.tocoo()

    # Add Mnew - M isolated vertices.
    rows = scipy.sparse.coo_matrix((Mnew-M,    M), dtype=np.float32)
    cols = scipy.sparse.coo_matrix((Mnew, Mnew-M), dtype=np.float32)
    A = scipy.sparse.vstack([A, rows])
    A = scipy.sparse.hstack([A, cols])

    # Permute the rows and the columns.
    perm = np.argsort(indices)
    A.row = np.array(perm)[A.row]
    A.col = np.array(perm)[A.col]

    assert np.abs(A - A.T).mean() < 1e-8 # 1e-9
    assert type(A) is scipy.sparse.coo.coo_matrix

1.3.4 构造图拉普拉斯矩阵

def laplacian(W, normalized=True):
    """Return graph Laplacian"""

    # Degree matrix.
    d = W.sum(axis=0)

    # Laplacian matrix.
    if not normalized:
        D = scipy.sparse.diags(d.A.squeeze(), 0)
        L = D - W
    else:
        d += np.spacing(np.array(0, W.dtype))
        d = 1 / np.sqrt(d)
        D = scipy.sparse.diags(d.A.squeeze(), 0)  # 构造对角稀疏矩阵
        I = scipy.sparse.identity(d.size, dtype=W.dtype)  # 构造单位矩阵
        L = I - D * W * D  # 构造标准化拉普拉斯矩阵

    assert np.abs(L - L.T).mean() < 1e-9
    assert type(L) is scipy.sparse.csr.csr_matrix
    return L

1.3.5 使用重边匹配构造K个粗化图

def coarsen(A, levels):
    
    graphs, parents = HEM(A, levels)
    perms = compute_perm(parents)

    laplacians = []
    for i,A in enumerate(graphs):
        M, M = A.shape
            
        if i < levels:
            A = perm_adjacency(A, perms[i])

        A = A.tocsr()  # 将矩阵转换为压缩形式
        A.eliminate_zeros()  # 删除零
        Mnew, Mnew = A.shape
        print('Layer {0}: M_{0} = |V| = {1} nodes ({2} added), |E| = {3} edges'.format(i, Mnew, Mnew-M, A.nnz//2))

        L = laplacian(A, normalized=True)
        laplacians.append(L)  # 将当前图的拉普拉斯矩阵加入列表
        
    return laplacians, perms[0] if len(perms) > 0 else None

perms存放的是进行边聚合后构造的二叉树，laplacians存放的是每一种粗化图对应的图拉普莱斯矩阵

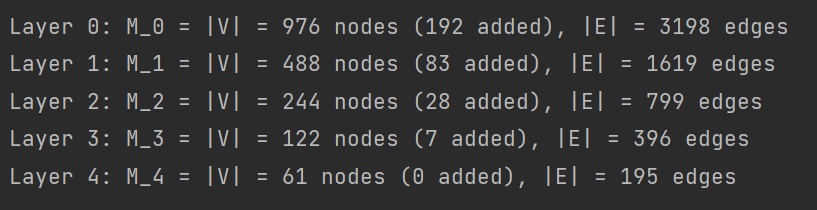
第一层代表总共有976个节点，其中192个节点是添加的呈中性的假节点（为构造二叉树用），原图真正的节点数976-192=784

1.4 计算每个粗话图的最大特征值

def lmax_L(L):
    """Compute largest Laplacian eigenvalue"""
    return scipy.sparse.linalg.eigsh(L, k=1, which='LM', return_eigenvectors=False)[0]

scipy.sparse.linalg.eigsh(A, k=6, M=None, sigma=None, which=‘LM’, v0=None, ncv=None, maxiter=None, tol=0, return_eigenvectors=True, Minv=None, OPinv=None, mode=‘normal’)
功能：找到实对称方阵或复杂厄米特矩阵的k个特征值，特征向量

1.5 根据二叉树节点索引重新索引数据集的节点索引，构造数据集二叉树

# Reindex nodes to satisfy a binary tree structure
train_data = perm_data(train_data, perm)
val_data = perm_data(val_data, perm)
test_data = perm_data(test_data, perm)

print(train_data.shape)
print(val_data.shape)
print(test_data.shape)

print('Execution time: {:.2f}s'.format(time.time() - t_start))
del perm